01 Speed of Light; Foucault-Michelson

Aim¶

To “measure” speed of light

Subjects¶

• 6A01 (Speed of Light)

Diagram¶

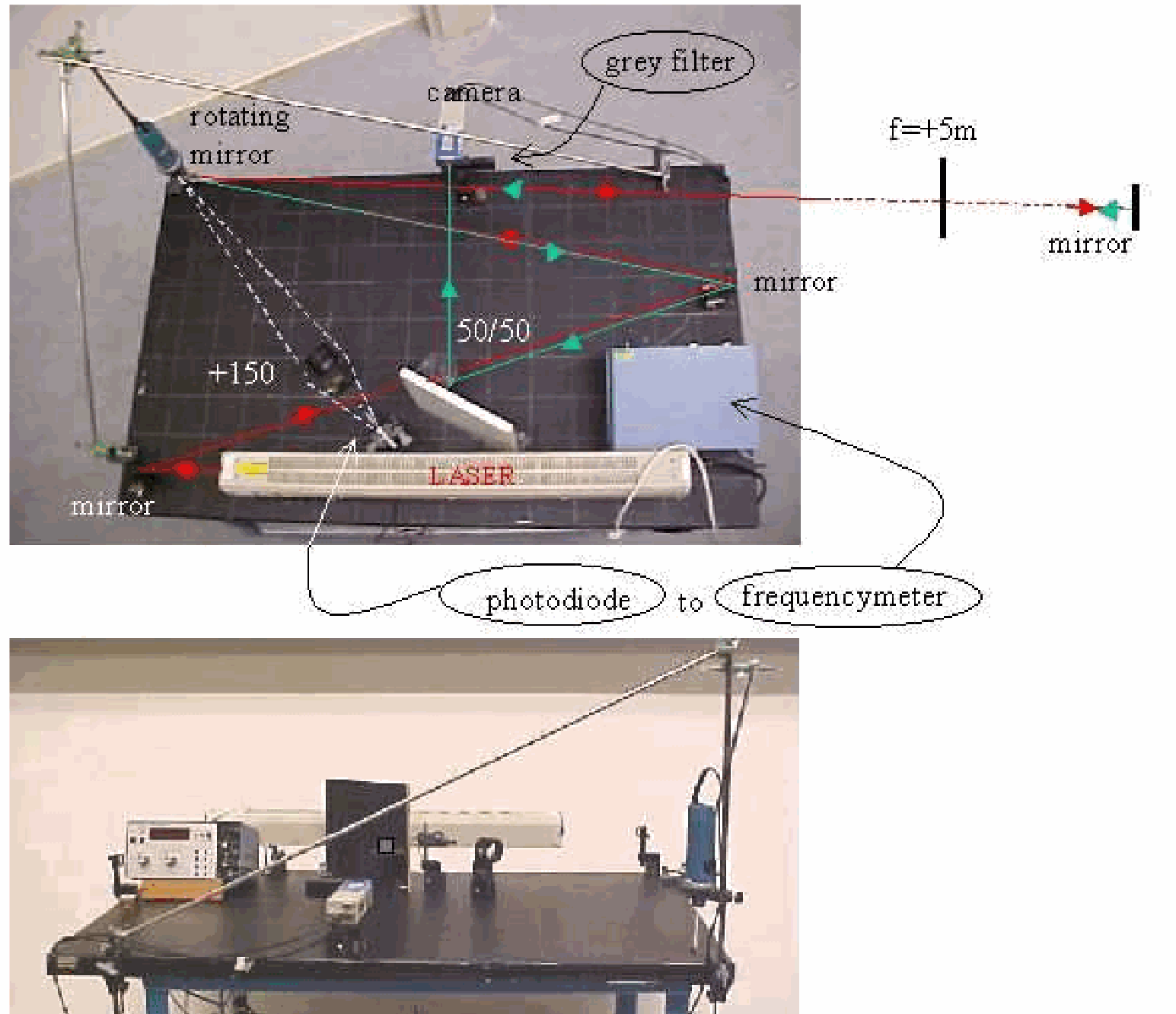
Equipment¶

• Optical components (see Diagram).

• Camera without lens (see Diagram).

• Variable transformer to supply the motor of the rotating mirror.

• 5Vdc to supply the photo-diode circuit.

• Monitor, connected to camera.

• Double overhead sheet, explaining the assembly.

Presentation¶

Preparation:¶

Make the laser beam go as horizontal as possible; careful alignment is essential in this demonstration. (Start at the laser and work step by step working yourself through the light path.)

The $+5 \mathrm{~m}$-lens is positioned at about $5 \mathrm{~m}$ distance from the rotating mirror.

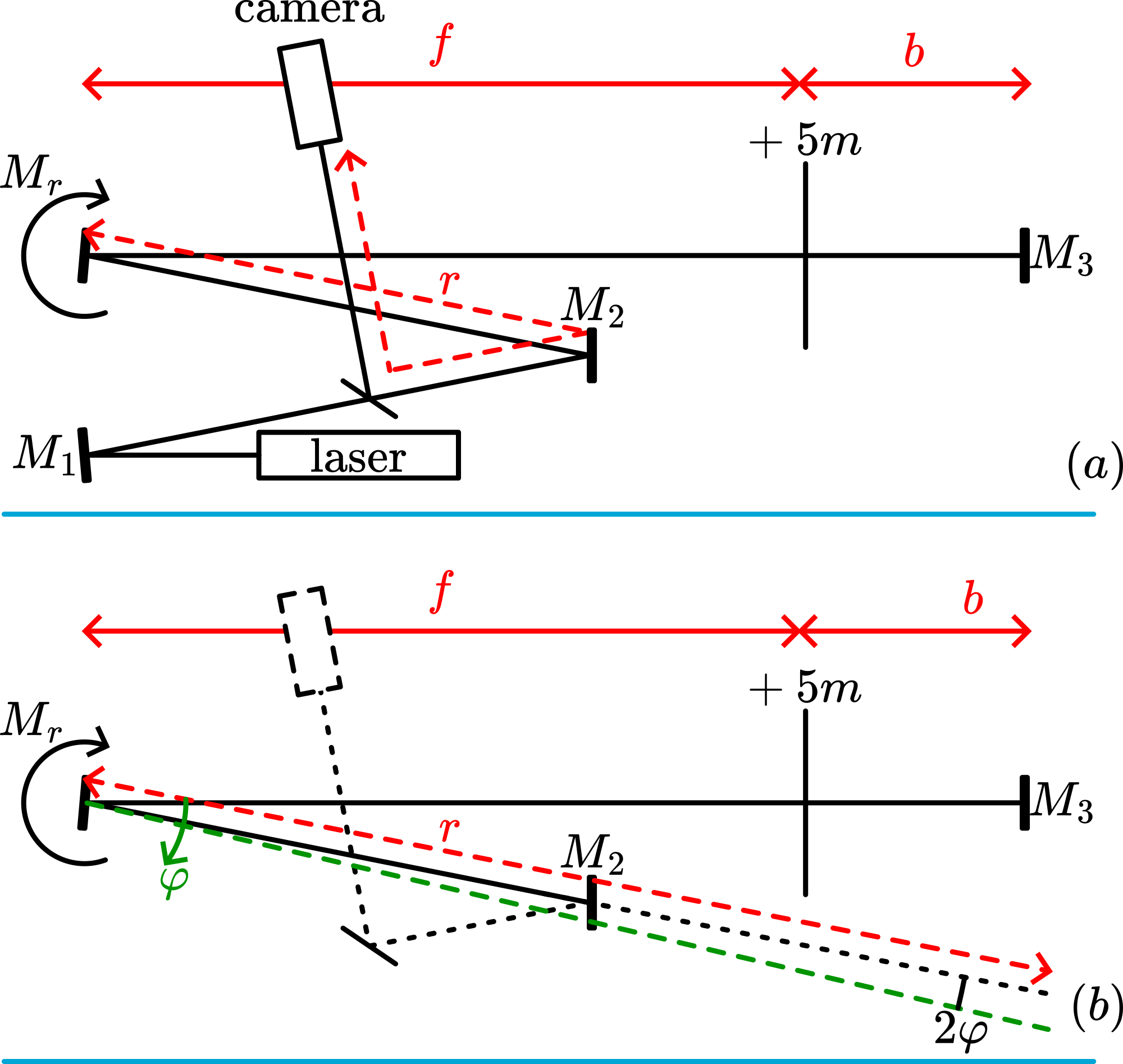
Image-distance $b$ (see Figure 2A) is chosen such that the image of the first mirror $\left(\mathrm{M}_{1}\right)$ is sharp at $M_{3}\left(\frac{1}{f}=\frac{1}{r+f}+\frac{1}{b}\right)$. (In our assembly this means that $b$ is around 25 meters.) Lens $+5 \mathrm{~m}$ and $M_{3}$ are carefully adjusted until, in the right postion of the rotating mirror $\left(M_{r}\right)$ the laserbeam is reflected to the camera (the camera and $M_{1}$ have the same distance to $\mathrm{M}_{3}$ ). Making the rotating mirror turn at its highest speed (about 500 rev. per second) the light spot displaces, in our assembly, the whole width of the monitor screen. This displacement is calibrated by placing a plastic ruler between the grey filter and the camera (see Figure 3A).

Shadow projection of the mm-lines on the sensitive layer of the camera show these lines on the monitor (we have $7 \mathrm{~mm}$ across the full width of the monitor screen; see Figure 3B). The geometry of the assembly makes it possible to link the rotation of the mirror to the displacement on the monitor screen (we have a displacement of around

$2.5 \mathrm{~mm}$ on the camera, corresponding to $\phi=\frac{d}{2 r}=\frac{2.5 \times 10^{-3}}{2 \times 2.6}=0.48 \times 10^{-3} \mathrm{rad}$ of $\mathrm{M}_{\mathrm{r}}$ ).

Demonstration:¶

The laser is switched on and the light path is shown to the students. By hand the rotating mirror is turned until a flash is seen on the monitor screen. In this position the light path is as drawn in the Diagram. The principle of operation is explained to the students: In the time it takes the light beam to travel the distance $M_{r}-M_{3}-M_{r}$ the rotating mirror has made a little angle ( $\varphi$ ). This is observed on the monitor screen (angle $2 \varphi$, see Figure 2B).

Also the calibration is explained to the students.

While the speed of rotation of $M_{r}$ increases the students see an increasing displacement of the light spot on the monitor screen. While running at a convenient speed (we use $n=500 \mathrm{~s}^{-1}$ to make calculations easy), this reading and that of the displacement on the monitor screen are used to calculate the speed of light.

Explanation¶

During the time ( $\Delta t$ ) it takes the light beam to travel the distance $M_{r}-M_{3}-M_{r}$ the rotating mirror has made a little angle $(\varphi)$ that is read from the monitor screen. Observing the speed of rotation on the frequency meter, the time it took to make this little angle can be calculated. For instance we measure when $M_{r}$ runs at $500 \mathrm{~s}^{-1}$, a light spot displacement of $d=2.5 \mathrm{~mm}$ on the monitor screen. This means an angle of rotation of that mirror of $\phi=\frac{d}{2 r}=\frac{2.5 \times 10^{-3}}{2 \times 2.6}=0.48 \times 10^{-3} \mathrm{rad}$. With $n=500 \mathrm{~s}^{-1}(500 \times 2 \pi \mathrm{rad} / \mathrm{sec})$

this means a time-span of $\Delta t=\frac{0.48 \times 10^{-3}}{500 \times 2 \pi}=0.15 \mu \mathrm{sec}$. (So, the displacement measurement on the monitor screen becomes in this way a $\Delta t$-measurement.) Our distance $\mathrm{f}+\mathrm{b}=23$ meter. This gives us $c=\frac{2 \times 23}{0.15 \times 10^{-6}}=3.1 \times 10^{8} \mathrm{~m} / \mathrm{s}$. (The measurement of the light spot displacement on the monitor screen is done very roughly, so our result of $\mathrm{c}=3.1 \times 10^{8} \mathrm{~m} / \mathrm{sec}$ is satisfying.)

Remarks¶

• Since 1984 the speed of light is a universal constant (having the exact value of $299792458 \mathrm{~m} / \mathrm{s}$; in vacuum). So principally it cannot be measured. Doing this experiment means measuring the distance $f+b$. But we just do the demonstration and “measure” the speed of light and in the end we mention this “complication” to the students.

• Measuring the speed of rotation with the photo-diode is complicated since the light spot sweeps very fast across the photo-diode. We use a $+150 \mathrm{~mm}$ lens to make the light spot stay longer on the photo-diode during its sweep (see Diagram).

• The “grey filter” shown in the Diagram is a variable neutral density filter used to adjust the light intensity to the camera.

Sources¶

• Hecht, Eugene, Optics, pag. 5

• Leybold-Heraeus, Physikalische Handblätter, pag. DK535.222;b