01 Damped Harmonic Motion

Aim¶

To show the effect of damping on amplitude and frequency of an oscillation.

Subjects¶

• 3A50 (Damped Oscillators)

Diagram¶

Equipment¶

• Track, $2.2\mathrm{~m}$.

• Cart.

• Motion sensor, mounted on cart.

• Reflecting screen.

• Two springs.

• Screen, ($50\times 50\mathrm{~cm^2}$; $m=0.5\mathrm{~kg}$) with socket screw.

• Socket head to mount screen on cart.

• Mass $m=0.5\mathrm{~kg}$.

• Pair of scales with large display.

• Photo-gate and laser.

• Data-acquisition system and software.

• Beamer to project the monitor-screen.

Presentation¶

Mount the cart with motion sensor and the mass of $.5 \mathrm{~kg}$ between the two springs that are attached to the end-stops of the track. Position the reflecting screen, needed for the motion sensor, at the end of the track. Place the photo-gate in such a position that the laser-beam just not touches the cart. The data-acquisition system is set so that collection of data starts as soon as the cart crosses the laser-beam. (See Diagram.) Prepare a graph to display position versus time (see Figure 2)

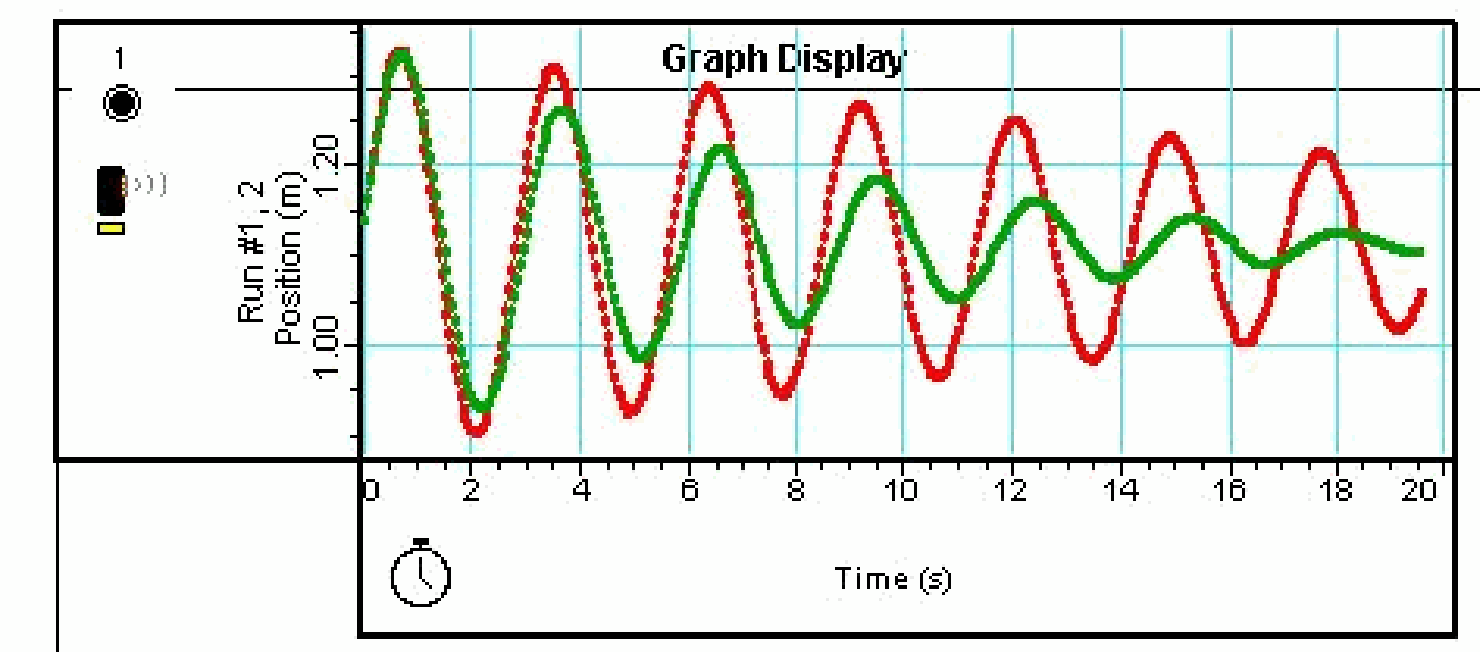
Give the cart a deflection, start the data-acquisition system and let the cart go. Data are collected during 20sec.

Remove the mass of $.5 \mathrm{~kg}$. Show by means of a pair of scales that the $50 \times 50 \mathrm{~cm}^{2}$ screen has also a mass of $.5 \mathrm{~kg}$. Mount the screen on the cart. Give the cart the same deflection as in the foregoing run, start the data-acquisition system and let the cart go. Again collect data during 20 sec.

The two graphs of position can be studied and discussed now (see Figure 2). Clearly can be observed that the screen on the cart introduces more damping to the oscillating system. Also can be seen that damping reduces the frequency of the oscillation.

Explanation¶

Damping happens due to resistance forces dissipating energy. Such forces can be described assuming that the magnitude of the resistance force is related to the speed of the body as $F=-b v^{n}$ ( $n$ is a number between 1 and 2; $b$ is the damping coefficient).

For many situations $n$ is given the extreme value of $n=1$, making the resistance force equal to $F=-b v$. Then for such a damped oscillator the position of mass $m$ can be expressed by $x=e^{-\alpha t} A \sin (\omega t+\varphi), \alpha=\frac{b}{2 m}$. Increasing $b$ (mounting the $50 \times 50 \mathrm{~cm}^{2}$-screen on the cart) means increasing $\alpha$ and so $e^{-\alpha t}$ decreases faster with time.

The angular frequency of a damped system equals $\omega=\sqrt{\omega_{0}^{2}-\frac{b^{2}}{4 m^{2}}}, \omega_{o}$ being the frequency in the absence of damping. So increasing $b$ means decreasing $\omega$. Comparing the period of the oscillations of the green line in Figure 2 with those of the red line, shows this clearly.

Sources¶

• Alonso, M/Finn, E. J., Fundamentele Natuurkunde, part 1, Mechanica, pag. 297-299

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 99-101

• Roest, R., Inleiding Mechanica, pag. 266-274

• Young, H.D. and Freeman, R.A., University Physics, pag. 411-412