04 Sonometer by Hand - The Demonstration Laboratory

Aim¶

To show the validity of the relationship between wavelength, string tension and linear density of the string.

Subjects¶

3B22 (Standing Waves)

Diagram¶

Diagram

Equipment¶

2 ropes ( $l=10\mathrm{~m}$ )
rope, four strings wrapped together ( $l=10\mathrm{~m}$ )
mass, $m=0.5\mathrm{~kg}$
mass, $m=2\mathrm{~kg}$
smooth bar

Presentation¶

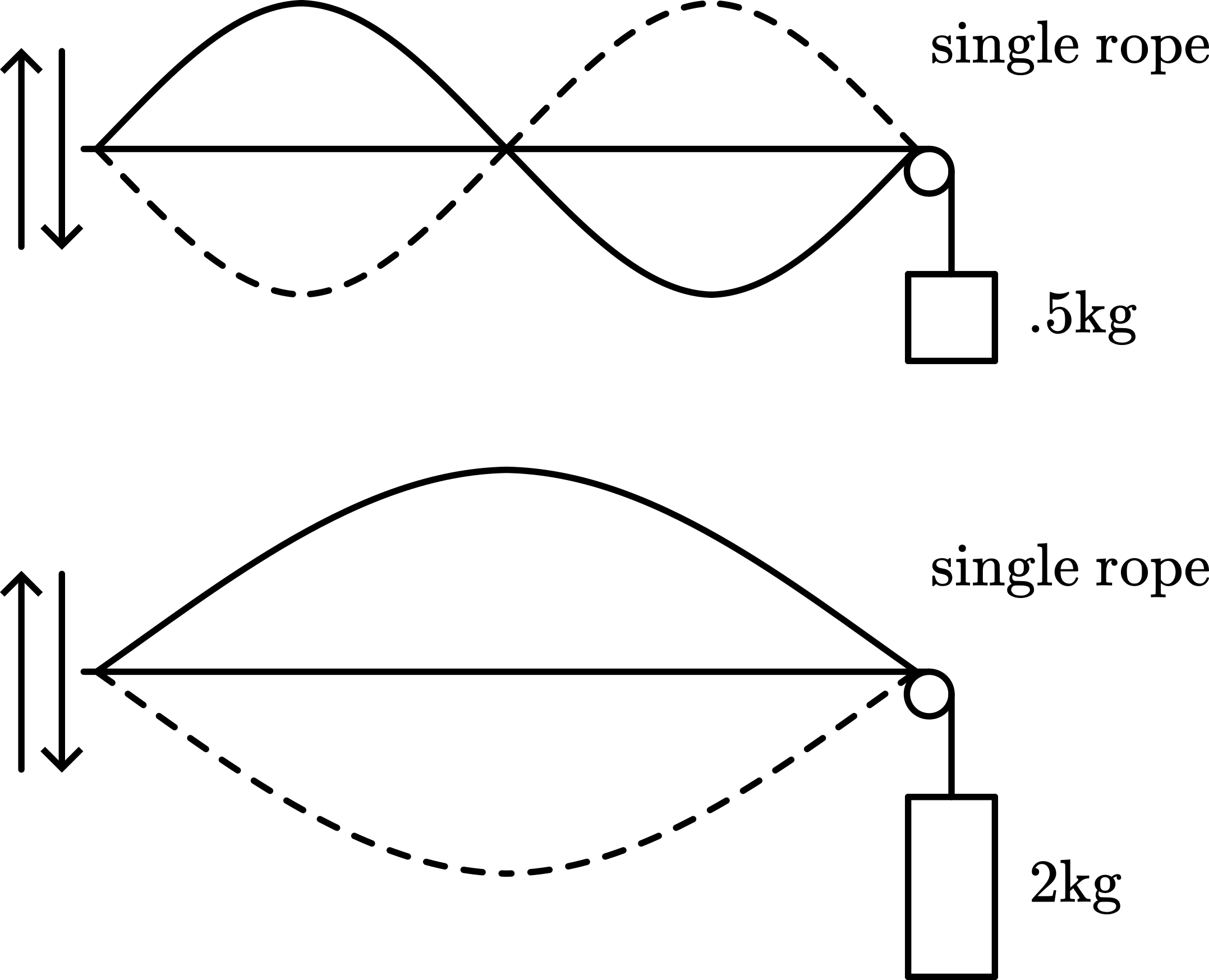
One rope is hung across the bar and loaded with $0.5 \mathrm{~kg}$ . The demonstrator graps the other end, standing about $8 \mathrm{~m}$ away and swings the rope vertically to a standing wave of one half wavelength. When he doubles his speed one complete wave appears in the rope.

With his other hand he also takes the second rope that is loaded with $2 \mathrm{~kg}$ . First he makes one complete wavelength in the rope that is loaded with $.5 \mathrm{~kg}$ . Then he starts moving the second hand in the same rhythm. A half wave will appear in this second rope (Figure 1).

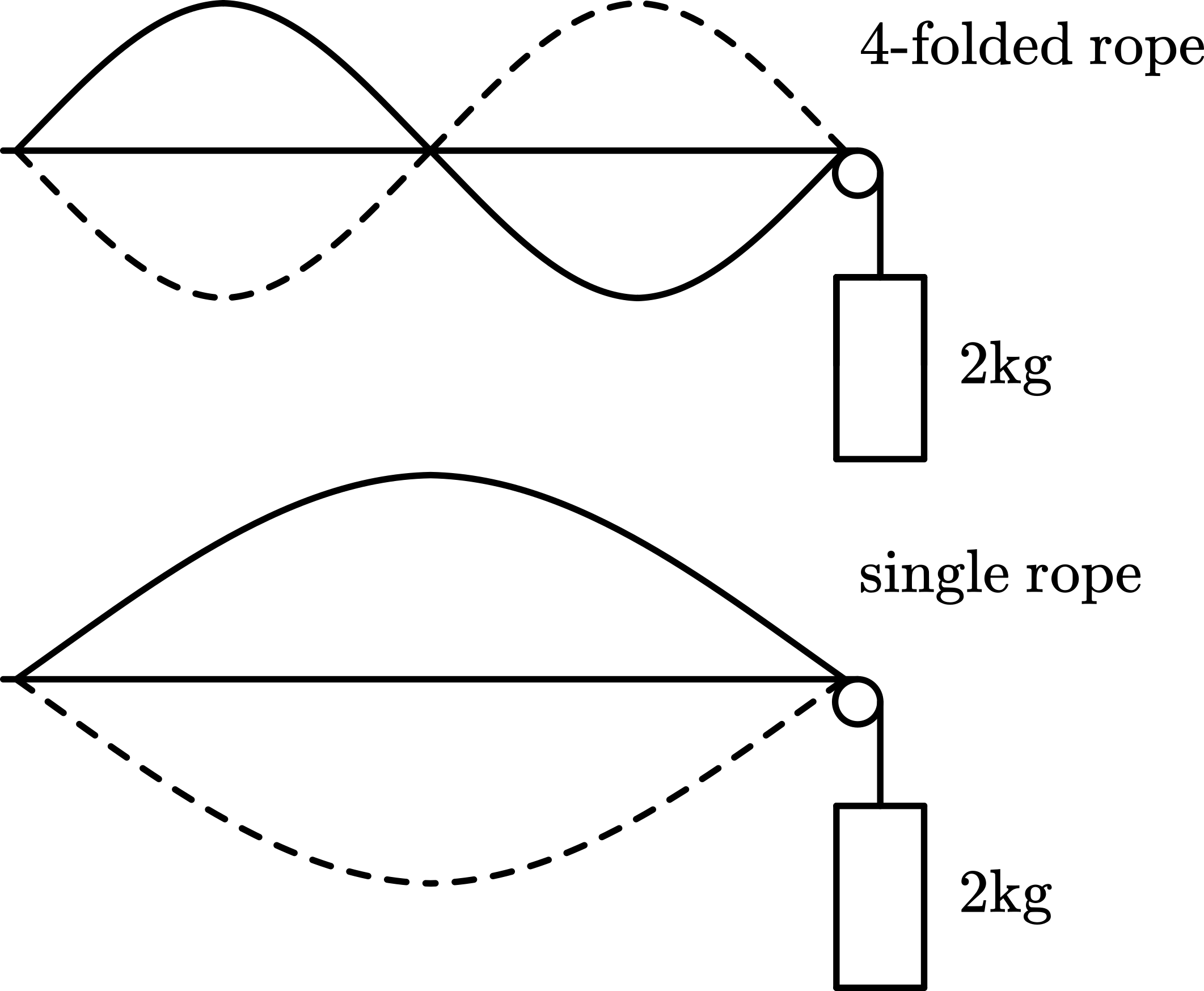
The demonstrator takes the rope that is four times as heavy and loads it with $2 \mathrm{~kg}$ . Slowly moving he makes a standing wave of one half wavelength. Doubling his speed, he makes a standing wave of one complete wavelength.

With his second hand he takes a single rope, also loaded with $2 \mathrm{~kg}$ and when this rope moves in the same rhythm as his first hand is doing for a complete wavelength, then a half wavelength appears in this second rope (Figure 2).

Explanation¶

For wave motion on a rope we can write $v=\frac{1}{\lambda} \sqrt{\frac{T}{\mu}}$ where,

$\nu=$ frequency of wave

$\lambda=$ wavelength

$T=$ rope tension

$\mu=$ linear density of rope

( $v=\sqrt{\frac{T}{\mu}}=$ velocity of wave propagation)

The first demonstration shows that, at the same frequency, $\lambda$ doubles when $T$ is four-folded.

The second demonstration shows that, at the same frequency and tension, $\lambda$ halves when $\mu$ is four-folded.

Remarks¶

Before demonstrating, take enough time to practice.
In our set-up it seems inevitable that a circular wave appears even when we strictly move our hands in a vertical plane. But this does not spoil the demonstration.

Sources¶

Giancoli, D.G., Physics for scientists and engineers with modern physics, pag. 405-408
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 344-345