02 Bungee Jumper

Aim¶

To show that a bungee jumper falls with an acceleration greater than $g$.

Subjects¶

• 1G10 (Force, Mass, and Acceleration)

• 1D40 (Motion of the center of mass)

Diagram¶

Equipment¶

• Chain, $l=6 \mathrm{~m}$, a wooden block fixed to the end.

• Double ladder.

• 2 wooden blocks.

• 2 wooden blocks, one painted red, the other yellow, and fixed to the chain.

• Clamping material to attach the chain to the ladder (see Diagram).

Safety¶

• In the pictures, the demonstrator is standing with his hands free. (We did so to make the picture clearer.) When you stand on the ladder, hold yourself!

Presentation¶

The ladder is set up, and the chain with the yellow block is attached to it. It hangs from such a height that the yellow block just touches the ground when the chain is fully extended (see Diagram A, where the end with the yellow block is temporarily fixed to the ladder).

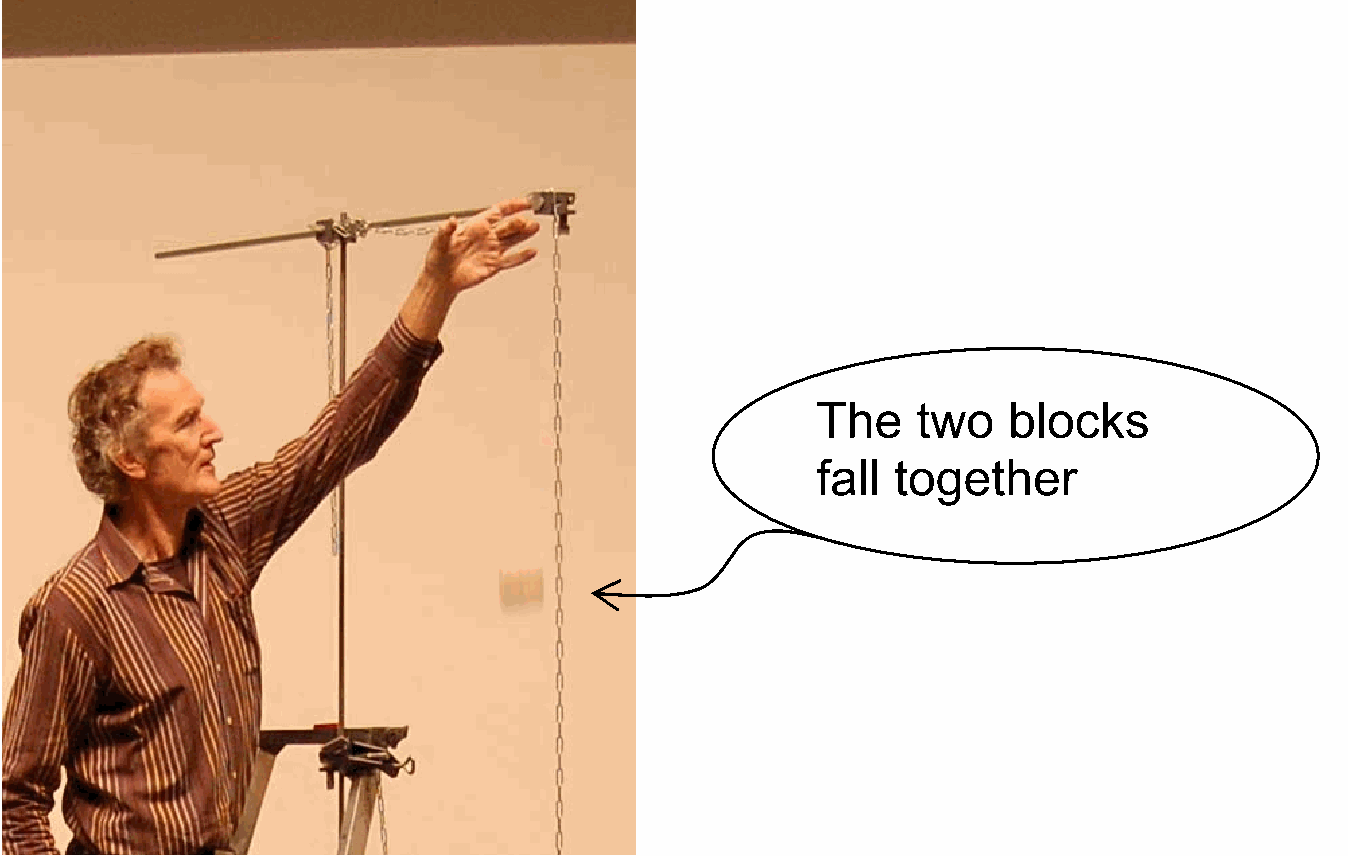
• Firstly, two small blocks of wood are kept fixed, squeezed between your thumb and forefinger. When you let them go, they fall together towards the ground and touch it at the same time (see Diagram B and Figure 2).

• The red and yellow blocks, which are attached to the chain, are held between your fingers (see Diagram C). Then, release them (see Diagram D) and observe that the yellow block touches the ground before the freely falling red block does. The difference in displacement can already be seen during the fall (see {numref}Figure {number} <1g1002_figure_2.png>), but it becomes especially clear at touchdown, when two distinct bumps are heard.

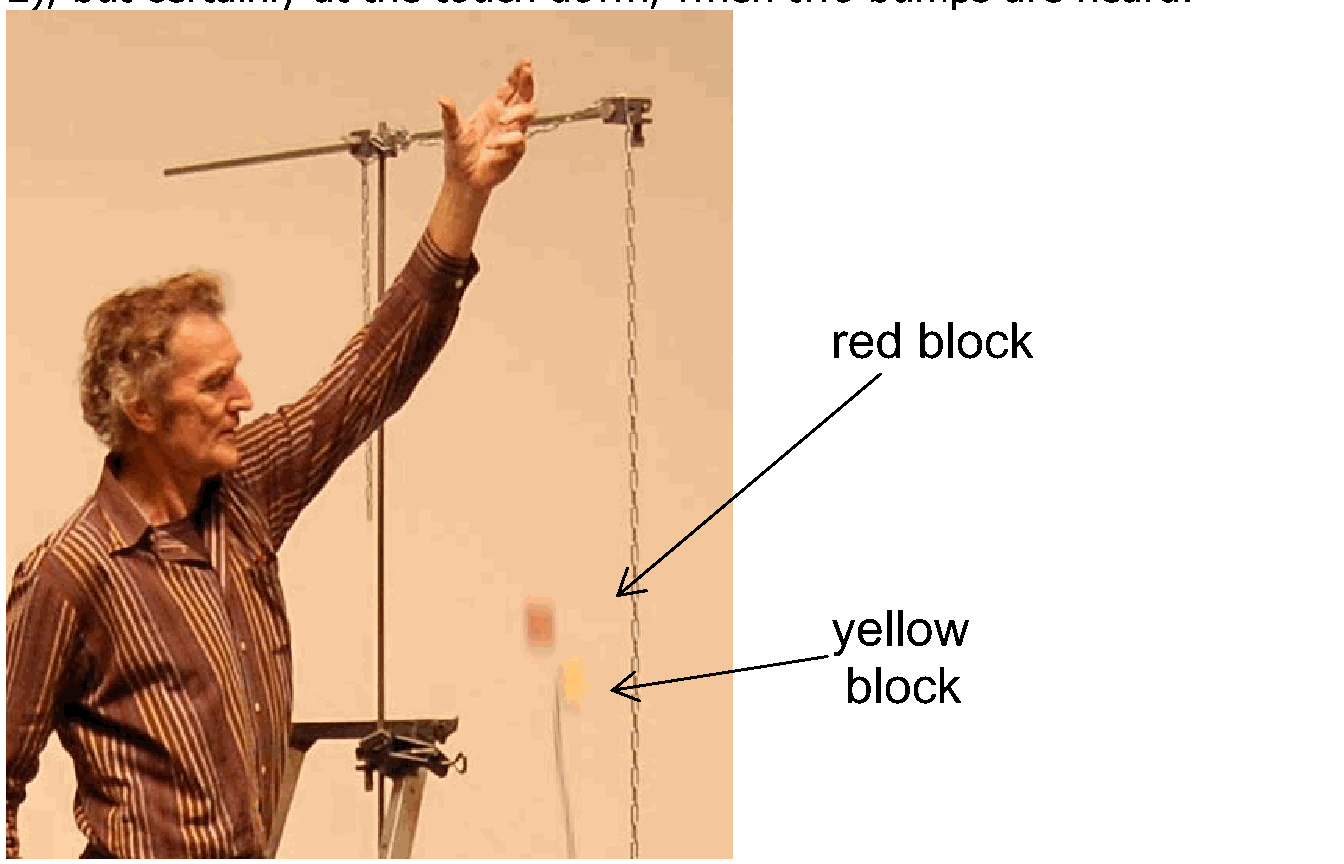
The block fixed to the chain reaches the ground before the free-falling block does. This means that the chained block has acceleration greater than $g$!

Explanation¶

The key to understanding the phenomenon is in recognizing that the mass of a real bungee cord is at least equal to the mass of the jumper. Therefore, the jumper on the end of the bungee cord can accelerate at a greater than $g$ acceleration because the center of mass of the system is not accelerating more than $g$.

Approaching the problem from the point of view of energy leads to an acceleration (at the end of maximum stretch) of $a=g\left[1+\frac{\mu(4+\mu)}{8}\right]$

where $\mu$ is the ratio of the mass of the cord to the mass of the jumper. (See Sources: The Physics Teacher) This equation shows that $a$ is always greater than $g$ and, depending on $\mu$, can be substantially greater than $g$.

An explanation through a force model is more difficult. In the indicated literature, some intuitive insights are gleaned from the following considerations:

• The motion of a bungee cord and jumper is similar to that of a whip. When a whip is cracked, energy from the entire whip is transferred via internal forces to the tip in such a way that initial speeds of a few meters per second become supersonic at the tip.

• Continuously, the portion of the chain at the bottom of the loop is coming to rest. Since it was moving downward, an upward force is required on this part of the system. Since this upward force is an internal force, and Newton’s Third Law must be satisfied, there must be an equal and opposite downward force somewhere within the system. A portion of this reaction force acts on the stationary part of the chain, but another part acts on the falling portion, causing it to accelerate.

• The falling portion of the chain can be thought of as a rocket moving downward. It is “ejecting” the chain as its “fuel” in such a way that the ejected chain is always at rest. So this ejected chain is “fired” upward, producing a downward “thrust” on the remaining portion of the moving chain.

Remarks:¶

• When the block is attached to the chain containing an acceleration sensor, its motion can be easily recorded using a data acquisition system. We often perform the demonstration this way, and the results align well with theoretical predictions.

• In this setup, no ladder is required. Dropping the block from a height of approximately 2 metres yields reliable results.

(Note: In this version of the demonstration, the block with the sensor is prevented from reaching the ground to protect the acceleration sensor.)

• As an alternative to using an acceleration sensor, the demonstration can also be performed with a Rotary Motion Sensor (see Sources: Pasco Newsletter).

Sources:¶

• Pronk, C./Biegstraaten,A.W.W.M., Syllabus “Inleiding Computergebruik”, pag. 191-218.

• American Journal of Physics, pag 776 (Vol. 74-9; 2006).

• Pasco Newsletter, Vol. 1/Issue 1 (Fall 09), pag. 6.