01 Brewster’s Angle (1)

Aim¶

To show the most common source of polarized light: polarization by reflection, as observed for the first time by Etienne Malus (1808).

Subjects¶

• 6H20 (Polarization by Reflection) 6H35 (Birefringence)

Diagram¶

Equipment¶

• Lamp, $12\mathrm{~V}$, halogen

• Transformer, $2-12\mathrm{~V}$.

• Resistor, $2 \Omega / 20 \mathrm{~W}$.

• Acrylic sheet (mirror).

• Camera.

• Calcite crystal.

• 30-60-90 triangle.

• Projector to project the camera-image.

Presentation¶

Etienne Malus was standing at the window of his house in the Rue d’Enfer (Paris) examining a calcite crystal. The sun was setting, and its image reflected towards him from the windows of the Luxembourg Palace not far away. He held up the crystal and looked through it at the sun’s reflection. To his astonishment, he saw one of the double images of the sun disappear as he rotated the calcite!

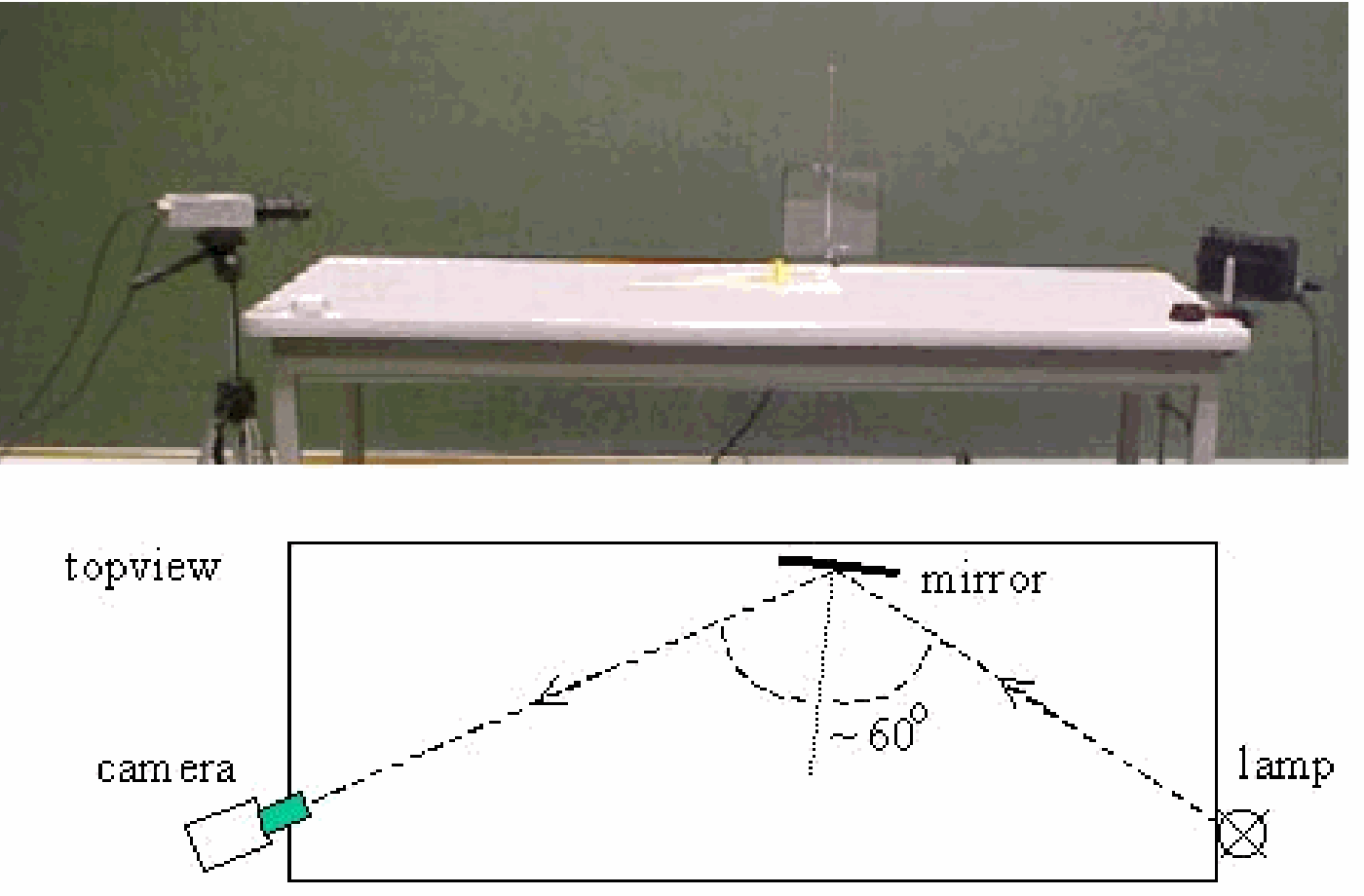
This historical situation is presented in our demonstration (see Diagram). The 12Vlamp is in our situation operating at $6 \mathrm{~V}$ in series with a $2 \Omega / 20 \mathrm{~W}$ resistor. This is the red glowing setting sun. The acrylic sheet is a window of the palace and the camera is the eye of Etienne Malus. The beamer projects to the audience the image that Etienne saw: “window” and reflected image of the “sun” (see Figure 2A). Take care that the camera is focussed on the light spot and not on the “window” itself.

The lay-out of the demonstration is such that the angle of incidence is about $60^{\circ}$. The large $30-60-90^{\circ}$ triangle shows this to the students. Now the calcite crystal is placed in front of the camera-lens (see Figure 2B). Everything in the projected image is doubled. While rotating the crystal also the double images rotate, but at two positions of rotation the doubling of the reflected “sun” disappears and only one “sun” is seen!
Observe also that the double image of the window never disappears.

Explanation¶

In the time of Malus the birefringent action of calcite was known (see the demonstration ‘Calcite crystal’ in this database). That Malus was experimenting with such a crystal was because the French Institute had offered a prize for a mathematical theory of the double refraction. In 1821 the work of, principally Thomas Young and August Fresnel finally led to such a mathematical theory: the representation of light as some sort of transverse vibration. The so-called Fresnel equations express the effect of an incoming (plane) wave falling on an interface between two different media. These equations relate the reflected and transmitted field amplitudes to the incident amplitude:

• When the $\mathrm{E}$-field is parallel to the plane of incidence (the so-called p-polarization), the reflection coefficient equals: $r_{p a r}=\frac{n_{t} \cos \theta_{i}-n_{i} \cos \theta_{t}}{n_{i} \cos \theta_{t}+n_{t} \cos \theta_{i}}$ and the transmittance

coefficient equals: $t_{\text {par }}=\frac{2 n_{i} \cos \theta_{i}}{n_{i} \cos \theta_{t}+n_{t} \cos \theta_{i}}$

• When the field is perpendicular to the plane of incidence (the so-called s-polarization): $r_{\text {perp }}=\frac{n_{i} \cos \theta_{i}-n_{t} \cos \theta_{t}}{n_{i} \cos \theta_{i}+n_{t} \cos \theta_{t}}$

and $t_{\text {perp }}=\frac{2 n_{i} \cos \theta_{i}}{n_{i} \cos \theta_{i}+n_{t} \cos \theta_{t}}$

Figure 3 shows these formulas in a graph (as function of the angle of incidence).

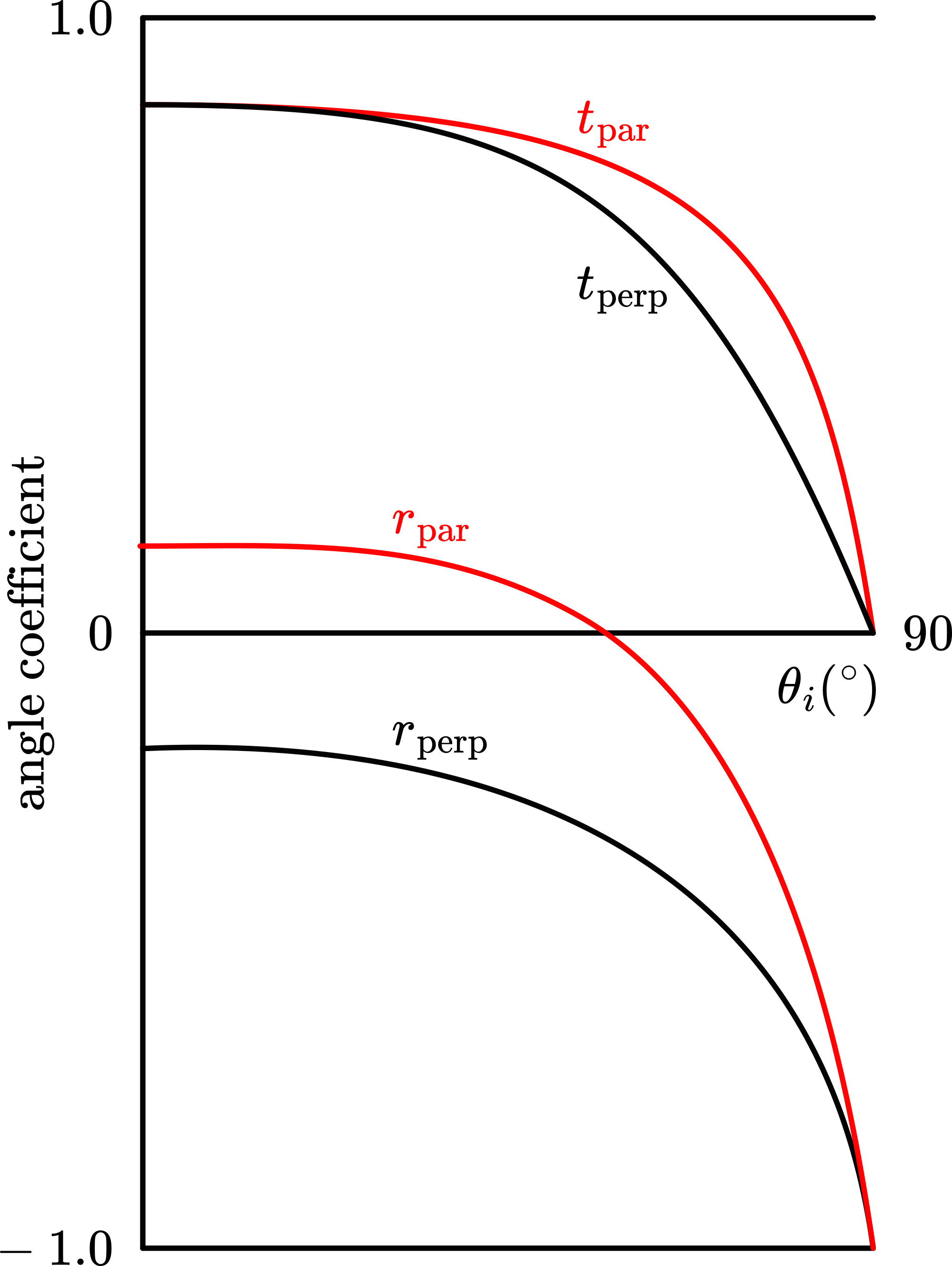
There appears zero amplitude for $r_{p a r}$ at a certain angle. This angle can be found when using Snell’s law in $r_{p a r}: r_{\text {par }}=\frac{\sin \theta_{i} \cos \theta_{i}-\sin \theta_{t} \cos \theta_{t}}{\sin \theta_{i} \cos \theta_{i}+\sin \theta_{t} \cos \theta_{t}}$. Rewriting (see textbooks) $r_{\text {par }}=\frac{\tan \left(\theta_{i}-\theta_{t}\right)}{\tan \left(\theta+\theta_{i} \theta_{t}\right)}$

This can be zero when the denominator is infinite, so when $\theta_{i}+\theta_{t}=90^{\circ}$. In this situation, using Snell’s law $n_{i} \sin \theta_{i}=n_{t} \sin \theta_{t}$ yields $n_{i} \sin \theta_{i}=n_{t} \cos \theta_{i}$, so $\tan \theta_{i}=\frac{n_{t}}{n_{i}}$, or $\theta_{i}=\arctan \frac{n_{t}}{n_{i}}$

This is Brewster’s law, formulated correctly in 1815. (Brewster was honoured half the prize of the French Institute in 1816.)

Acrylic sheet has $\mathrm{n}=1.5$, so here Brewster’s angle is: $\theta_{t}=56^{\circ}$. This is in correspondence with our setting up of the demonstration (angle of incidence is set at about $60^{\circ}$ ).

Remarks¶

• In this demonstration the historical approach is chosen in order to intensify the astonishment aroused by the phenomenon (the doubling of the sun that vanishes, but not so the doubling of the window).

• It is a lucky incident that Malus lived at the right spot to have Brewster’s angle at his position relative to the Luxembourg Palace.

• Mention also to the students that Fresnel is long before electromagnetic field theory. In those days their theory mentioned “luminous waves” and “ethereal vibrations”.

• Before doing this demonstration the birefringent crystal calcite should be introduced to the students. You can use the demonstration “Calcite crystal” in this database.

• Since we work in this demonstration with the amount of light our eyes see, we should work with the squares of the field amplitude, finally leading to $\theta_{i}=\arctan \frac{n_{t}}{n_{i}}$. This produces the same results.

• When electromagnetic theory is known to the students the situation of $\theta_{i}+\theta_{t}=90^{\circ}$ in Brewster’s law can be explained: The refracted wave entering the medium drives the bound electrons and they in turn reradiate. A portion of that re-emitted energy appears in the form of a reflected wave. If the situation is arranged so that $\theta_{i}+\theta_{t}=90^{\circ}$, the reflected wave vanishes, since linear oscillating charges will not emit in their direction of oscillation. This happens at Brewster’s angle (see also the second figure in [Brewster’s angle (2)](../6H2002 Brewsters Angle/6H2002.md) in this database and the demo [Brewster’s angle (3)](../6H2003 Brewsters Angle/6H2003.md)).

Sources¶

• Hecht, Eugene, Optics, pag. 111-115; 342-346; 658-659.