10 Rolling Up-and-Down, Again and Again

Aim¶

Determining the coefficient of rolling friction and to give an impression how low the coefficient of rolling friction is.

Subjects¶

• 1K20 (Friction)

Diagram¶

Equipment¶

• U-shaped railtrack

• Metal ball

Presentation¶

Release the ball and it will roll down the track, climb the other track, and so on. But gradually the distance it rolls reduces (due to rolling friction).

After $\mathrm{n}$ runs the coefficient of rolling friction can be determined by measuring the distance the ball travels upward in the $\mathrm{n}$-th run.

Explanation¶

The potential energy of the ball equals (see Figure 2 and Figure 3)

$U_{p}(0)=m g s_{0} \sin (\alpha)=F s_{0}$

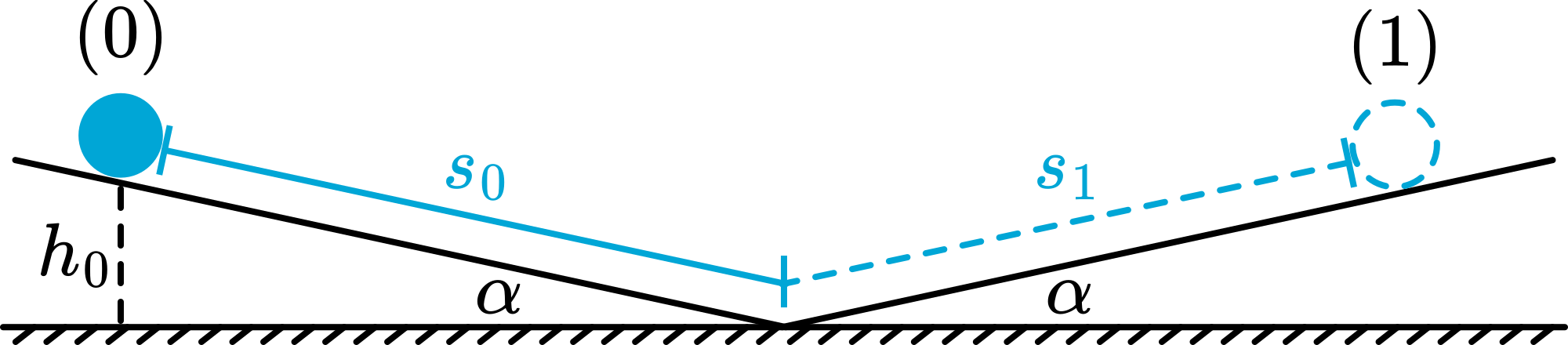
Reacting the other side (1): $U_{p}(0)-U_{p}(1)=F_{f}\left(s_{0}+s_{1}\right)$

So: $F\left(s_{0}-s_{1}\right)=F_{f}\left(s_{0}+s_{1}\right)$

$s_{1}=s_{0}\left[\frac{F-F_{f}}{F+F_{f}}\right]=s_{0}\left[\frac{1-\frac{F_{f}}{F}}{1+\frac{F_{f}}{F}}\right]=s_{0} b$

Rolling back ( $\mathrm{s}_{1}$ ) and up ( $\mathrm{s}_{2}$ ) again:

$s_{2}=s_{1} \cdot b=s_{0} \cdot b^{2}$

The coefficient of friction $(\mu)$ is by definition $F_{f} / F_{N}$.

In this case (see Figure 3): $\mu=\frac{F_{f}}{F} \tan \alpha$.

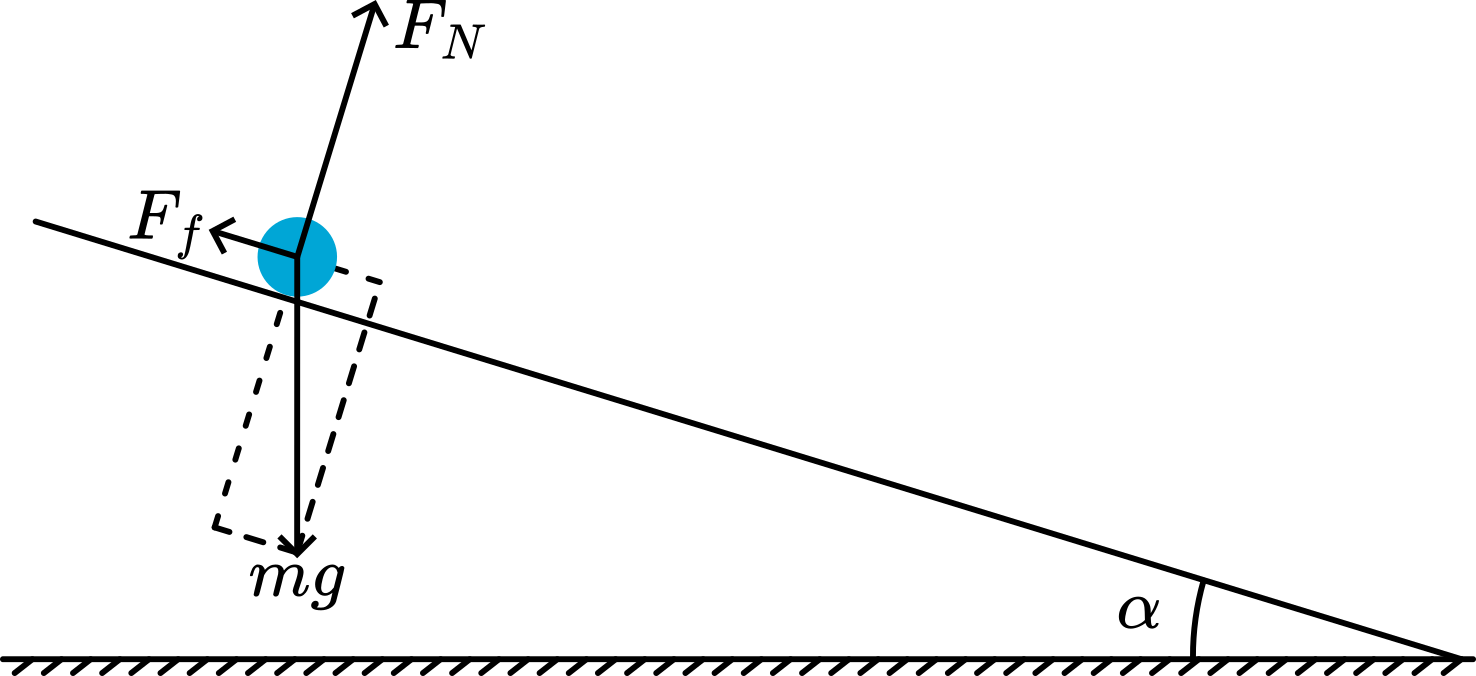
So the coefficient of friction can be determined by measuring $s_{0}, s_{2}$ and $\alpha$ and using the formulas above.

Sources¶

• Jordens, H.