02 Yo-Yo

Aim¶

To show the movement of a yo-yo and the force it exerts on the string that is holding it.

Subjects¶

• 1Q20 (Rotational Energy)

Diagram¶

Equipment¶

• Yo-yo.

• Force sensor.

• Data-acquisition system.

• Projector to project monitor image.

Presentation¶

We all know the yo-yo: Two circular discs with a common shaft and a string several times wrapped around it. Hold the end of the string stationary and release the yo-yo. The string unwinds as the yo-yo drops and rotates with increasing speed. When the unwrapping is completed, the yo-yo climbs again, comes to a stop and starts over again. etc.

Suspending the yo-yo to a force sensor, a registration of the tension in the string is made (red graph in Figure 2 left). When, finally, the yo-yo has come to rest, such a registration is repeated (green line in Figure 2 left).

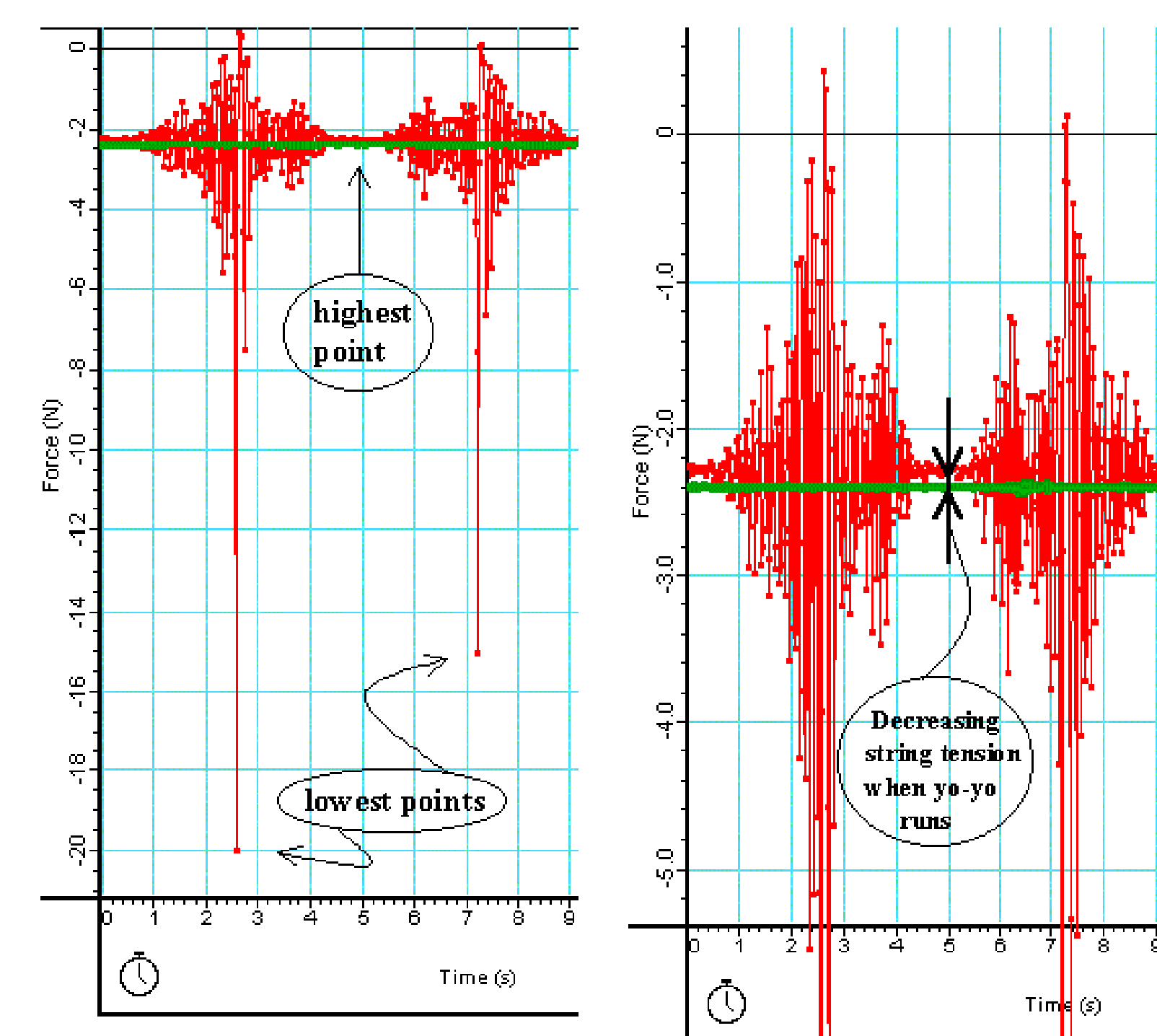
When studying these graphs, the jerk at the turning point is clearly observed. (Also a strong vibration.) See that the jerk at the turning point is much higher than the weight of the yo-yo.

Going from one jerk to the next, the highest position of the yo-yo is halfway between the two jerks. When a complete cycle is enlarged (see Figure 2 right), it is clear that during the complete cycle the string tension is lower than the weight of the yo-yo.

Explanation¶

The yo-yo accelerates (a) due to a force $m a=m g-F_{s}\left(F_{s}\right.$ being the string tension and $m$ the mass of the yo-yo.)

When there is no string, then $F_{s}=0$ and $a=g$ (free fall);

With a string, $a$ is always smaller than $g$ :

$a=g-\frac{F_{s}}{m}$

When $F_{s}$ is just a little smaller than $m g$, then $a$ will be very small.

The angular acceleration $(\alpha)$ of the roll during its fall can be found from $\alpha=\frac{\tau}{I}$, where

the net torque $(\tau)$ is given by $\tau=m g$.

The acceleration of the center of mass (a) is related to the angular acceleration of the yo-yo by $a=\alpha r$, so the yo-yo accelerates downward by $a=\frac{m g r^{2}}{I}$.

Our yo-yo is a simple double disc, so $I_{C M}=\frac{1}{2} m R^{2}$. It rolls at the circumference of the shaft (radius $r$ ), that’s why $I=\frac{1}{2} m R^{2}+m r^{2}$, and we find for the acceleration:

$a=\frac{2 g}{2+\frac{R^{2}}{r^{2}}}$.

Because $R>>r, a<<g$.

With our yo-yo we have $R=150 \mathrm{~mm}$ and $r=12 \mathrm{~mm}$, so $a=0.012 \mathrm{~g}$.

Also the string tension can be calculated now: $F_{s}=m g-m a$, so: $F_{s}=m g-0.012 m g$, showing that the string tension is just a little lower than the weight of the yo-yo.

Remarks¶

• A worthwhile observation is, that when the string is unwrapped completely and the yo-yo starts climbing again, that the yo-yo’s translational velocity changes its direction $(-v$ to $+v)$ but keeps its rotation in the same direction. In other words: its momentum changes direction ( $-m v$ to $+m v$ ), but there is no change in angular momentum. The large change of momentum ($2mv$) at this point of the yo-yo’s movement explains the jerk (the change of momentum takes place in a very short time).

• See also the demonstration Maxwheel in this database in order to link the measured string tension to the acceleration of the yo-yo. Usually we show these two demonstrations together.

Sources¶

• Borghouts, A.N., Inleiding in de Mechanica, pag. 186-187

• Roest, R., Inleiding Mechanica, pag. 183-185

• Young, H.D. and Freeman, R.A., University Physics, pag. 303