Skip to article frontmatterSkip to article content

07 Dumb-Bell

Aim

To show that change in direction of angular momentum needs a torque.

Subjects

Diagram

.

Figure 1:.

Equipment

Presentation

The dumbbell is placed on top of the support. A thread is fixed to the center of mass and thrown over the top of the frame and hold slack, away from the dumbbell. The dumbbell is given a rotation by hand. Make the students observe that the two masses of the rotating dumbbell describe two horizontal circles (Figure 2a).

.

Figure 2:.

Lift the dumbbell from its support. Almost immediately it can be seen that now the rotation of the dumbbell takes place in one slanting plane (Figure 2b).

Before lift-off it can be seen that while the dumbbell rotates, the vertical support shaft oscillates/shakes/wobbles strongly and yet it is a thick and strong steel shaft!

Explanation

The dumbbell-shaped object rotates about a non-symmetry axis through the center of mass O. Figure 3a shows the angular momentum vector of the rotating dumbbell relative to O\mathrm{O} at the instant drawn and while the dumbbell rotates the angular momentum vector describes a cone. So the angular momentum changes direction continuously. To do this a torque is needed. The ballbearing support at O gives that torque: A centripetal force FcF_{c} is needed to move mm around in a circle (see Figure 3b). This needs a torque F⃗c×r⃗\vec{F}_{c} \times \vec{r}. (Also M⃗=dL⃗dt\vec{M}=\frac{d \vec{L}}{d t} gives this result.)

.

Figure 3:.

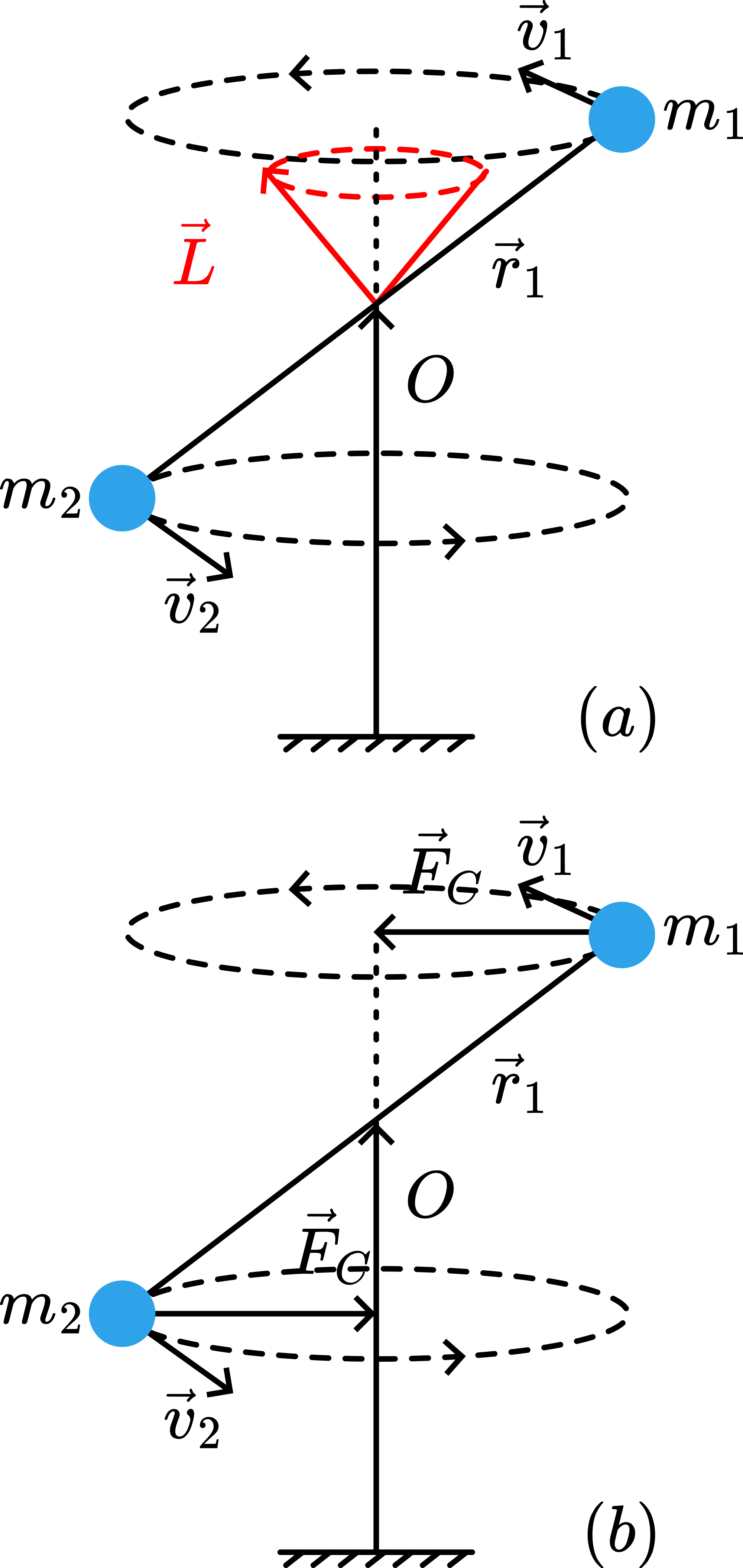
This torque also makes the support shaft wobble. The dumbbell needs to rotate in such a way as the direction of L⃗\vec{L} dictates at the moment of lift-off.

Remarks

Sources

1Q40 Conservation of Angular Momentum
06 Counter Rotating Disks
1Q40 Conservation of Angular Momentum
08 How an Astronaut can Turn Around in Free Space