09 Precession (3b)

Aim¶

To show how a rotating wheel reacts to an applied torque.

Subjects¶

• 1Q50 (Gyros)

Diagram¶

Equipment¶

• bicycle wheel with handles

• rotating platform

• support rods and clamps

• rotatable (hinged) clamp

Presentation¶

The bicycle wheel with handles is vertically mounted on a rotating platform in such a way that one handle is fixed in a hinged clamp and the other handle rests on a support (see diagram). The bicycle wheel is made fast spinning.

Now the rotating platform is slowly turned round by hand, trying both directions of rotation. In one direction of rotation, the spinning bicycle wheel will lift its free handle upwards from the support.

As soon as you stop speeding up the rotating platform, the lifting of the spinning bicycle wheel will stop also.

Leaving the spinning bicycle wheel to itself now, it slowly comes down, and the rotating platform speeds up.

Explanation¶

The spinning bicycle wheel has an angular momentum of $I_{1} \omega_{0}$. Rotating the platform, introduces a torque $T$. This torque tends to change $I_{1} \omega_{0}$, so $I_{1} \omega_{b}$ moves into the direction of $T$. So, when $T$ is pointing upward, $I_{1} \omega_{0}$ moves upward: the bicycle wheel handle lifts itself from the support. (See Figure 2a.)

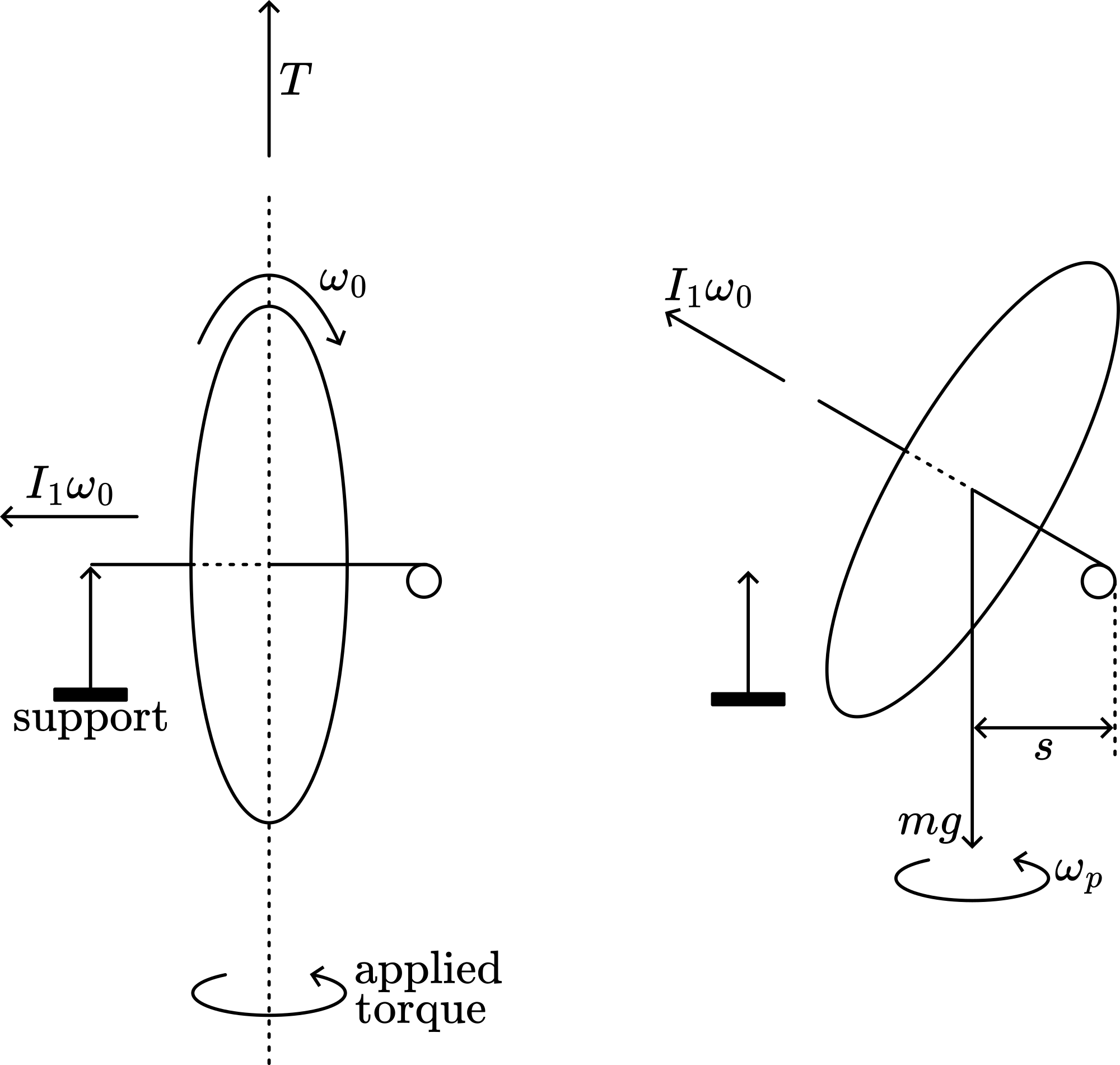
While the platform is freely rotating, gravitational torque $m g s$ is acting (see Figure 2b). In Figure 2b this torque is pointing out to the reader. $I_{1} \omega_{0}$ moves into the direction of $m g s$, keeping the platform rotating (precession). In this process, increases because the bicyclewheel is coming down. Since $\omega_{p}=\frac{m g s}{I_{0} \omega_{0}}, \omega_{p}$ increases due to $s$ becoming larger (and also a little due to $\omega_{0}$ becoming smaller).

Remarks¶

• Our setup is in such a way that $s$ changes substantially when the wheel comes down. When our wheel is at about $45^{\circ}, s=0$.

• Take care that the bicycle wheel is not lifted more than $45^{\circ}$, because then it surpasses the hinge and falls down to the other side, slamming the support-rods and clamps!

Sources¶

• Sutton, Richard Manliffe, Demonstration experiments in Physics, pag. 79