04 Percussionpoint (1)

Aim¶

To show the behavior of a stick to a short impulse.

Subjects¶

• 1Q60 (Rotational Stability)

Diagram¶

Equipment¶

• Platform with grid, used as reference.

• Ruler, $1 \mathrm{~m}$.

• Stick.

Presentation¶

1. Place the ruler with its centerline on the thick centerline of the grid (see Diagram). With the stick you give a short blow to the center of the stick (a movement like you are playing pool-billiards). There will result a translation of the stick.

2. Again place the ruler with its centerline on the grid. With the stick you give a short blow to the ruler e.g. at $60 \mathrm{~cm}$. There will result a translation and rotation of the stick.

3. With the stick you give a short blow to the ruler at $100 \mathrm{~cm}$. There will result a translation and rotation of the stick. Special is that it rotates around the point of $33 \mathrm{~cm}$ on the ruler.

4. With the stick you give a short blow to the ruler at $67 \mathrm{~cm}$. There will result a translation and rotation of the stick. Special is that it rotates around the beginning of the stick.

The point, around which the stick rotates is called “percussion point”. In point 3 and -4 , this point is on the stick; in point 2 it is outside the stick.

Explanation¶

Due to the short blow, the ruler performs a movement that can be considered as consisting of two movements: a translation and rotation around its center of mass $\mathrm{~CM}$ (see Figure 2).

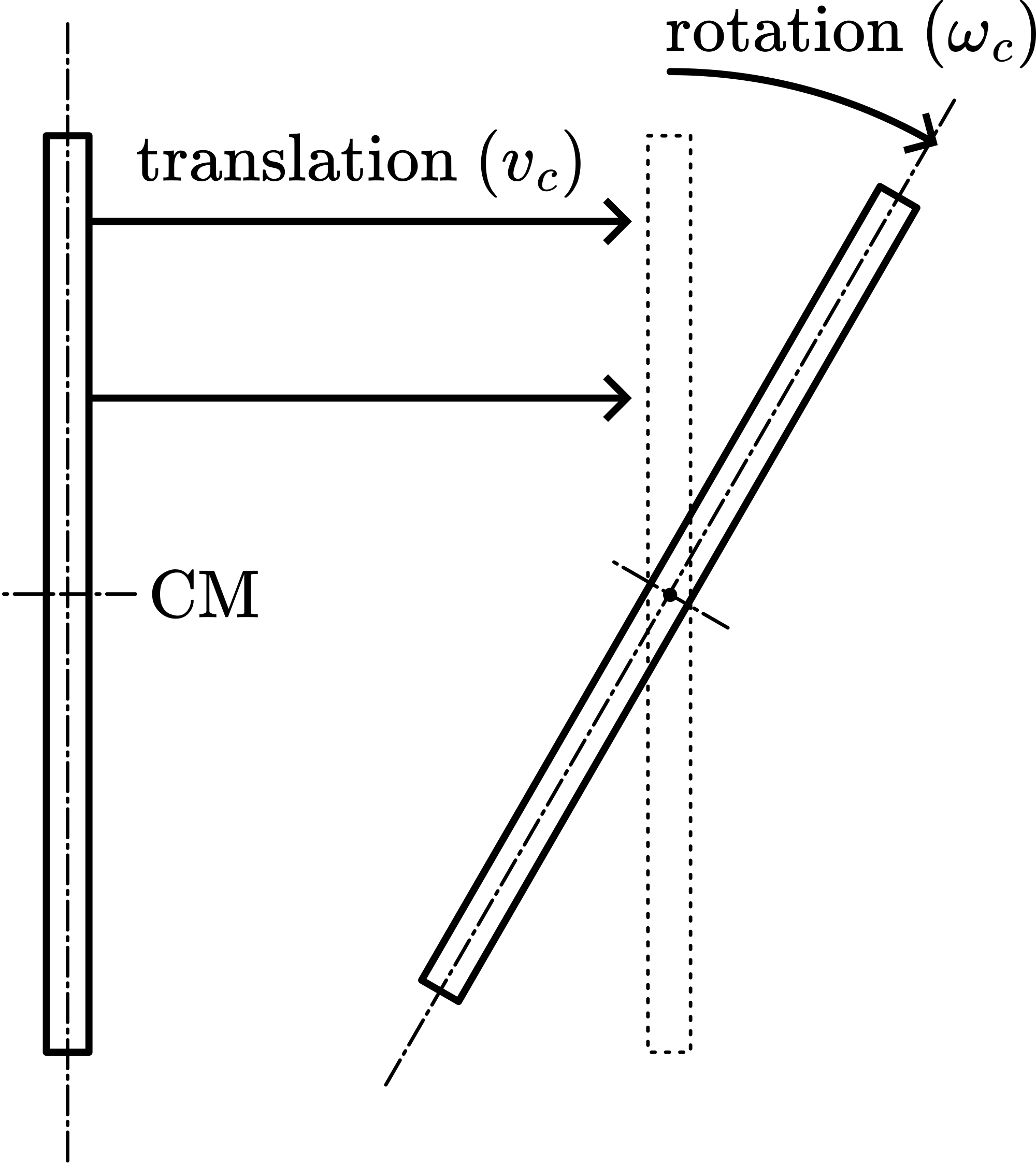
During the short blow force acts on the ruler. The total momentum of this force is $\int F dt=p$. The ruler gets a speed $v_{c}$, so the momentum of the ruler is $m v_{c}$. This makes $v_{c}=p / m$.

Relative to $\mathrm{CM}$ the ruler has also an angular momentum $I_{c} \omega_{c}=b p$ (see Figure 3). So $\omega_{c}=b p / I_{c}$ On one side of $\mathrm{CM}, v_{c}$ and $\omega_{c}$ have the same direction; on the other side $v_{c}$ and $\omega_{c}$ are opposite to each other. Looking at point A: $v_{A}=v_{c}-\omega_{c} x$. When point A remains at rest after the blow (A is then the so-called percussion point) then $0=v_{c}-\omega_{c} x$. This happens at $x=\frac{v_{c}}{\omega_{c}}=\frac{p / m}{b p / I_{c}}=\frac{I_{c}}{m b}$. For this ruler: $I_{c}=1 / 12 m l^{2}$, making $x=\frac{1}{12} \frac{l^{2}}{b}$.

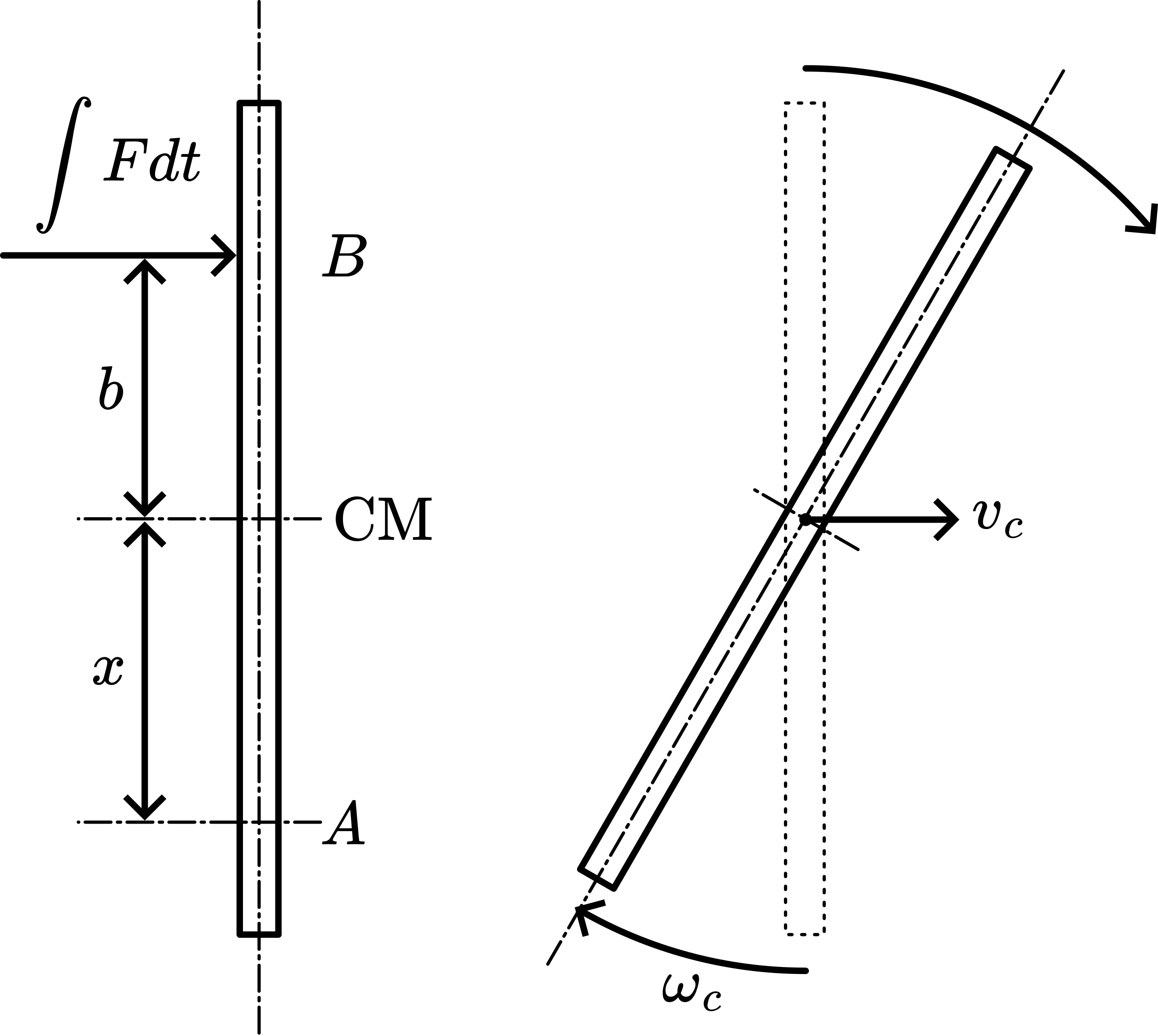
Applying this to the different situations of the Presentation shows the observed percussion points: in PresentationXX point 1 $(b=0)$, point 3 $(b=.5 \mathrm{~m})$ and point 4 $(b=.17 \mathrm{~m})$. In PresentationXX $(b=.1 \mathrm{~m})$, the percussion point is outside the ruler $(x=.83 \mathrm{~m})$.

Remarks¶

• Playing billiards with a stick instead with a ball needs practice!

Sources¶

• Borghouts, A.N., Inleiding in de Mechanica, pag. 182-183

• Roest, R., Inleiding Mechanica, pag. 172-173 and 176-177