01 Physical Pendulum (1) Compound Pendulum

Aim¶

To show and discuss the characteristics of a physical pendulum: reduced length, reversion pendulum and minimal period.

Subjects¶

• 3A15 (Physical Pendula)

Diagram¶

Equipment ’¶

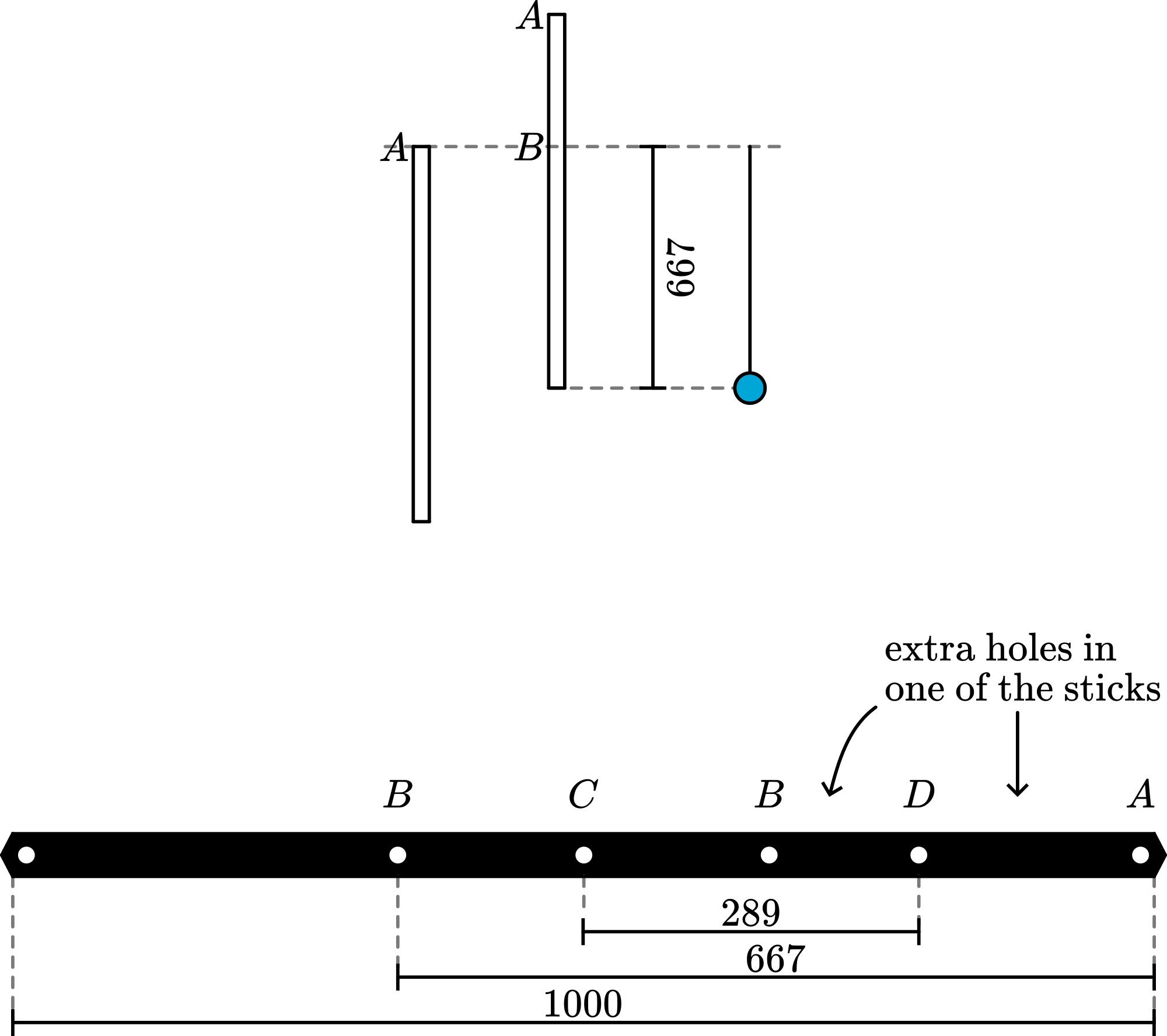
• 2 meter sticks; $I=1 \mathrm{~m}$, with holes for reversed pendulum and minimum pendulum. (One of the sticks has extra holes at $s=20 \mathrm{~cm}$ and $s=40 \mathrm{~cm}$ (see PresentationXX 3.)

• 2 axes in a ball-bearing.

• 1 mathematical pendulum ( $l=.667 \mathrm{~m}$ ).

• 1 meter stick for measurements.

Presentation¶

1. The physical pendulum is suspended on an axis at hole A. A mathematical pendulum is swinging and given such a length that its period equals that of the physical pendulum. Its length is measured and it shows $67 \mathrm{~cm}$.

2. Now the physical pendulum is suspended on the axis at hole $B$. Its period shows to be the same as both foregoing pendulums. The length of the pendulum below $B$ is measured and it shows that this length equals the length of the mathematical pendulum!

3. The pendulum is suspended at hole $D$. Now $T$ is shorter than in the foregoing demonstrations. Evidently there is a minimum between A and B.

   This can be demonstrated when both pendulums are suspended: one at $D$ and the other in one of the extra holes on either side of $D$ (between $A$ and B). When both pendulums start together, after only a few oscillations it is clear that $D$ is the faster pendulum.

Explanation¶

1. For a physical pendulum with mass $m$, oscillating around its suspension in point A, we can write for the period: $T=2 \pi \sqrt{\frac{I_{A}}{m g S}}$ (see Figure 2 $I_{A}$ being the moment of inertia, and $s$ being the distance between the centre $l_{M}$ of mass and the axis of rotation).

   When the physical pendulum is a long uniform stick of length $l_{F}$ its moment of inertia is $I_{c}=\frac{1}{12} m l_{F}^{2}$ and when it oscillates around a point A a distance $s=\frac{1}{2} l_{f}$ away from $C$, then $I_{A}=\frac{1}{12} m l^{2}+m\left(\frac{1}{2} l\right)^{2}$, so: $I_{A}=\frac{1}{3} m l_{F}^{2}$. The period of the pendulum becomes:

   $$T_{F}=2 \pi \sqrt{\frac{\frac{1}{3} m l_{F}^{2}}{\frac{1}{2} m g l_{F}}}=2 \pi \sqrt{\frac{2}{3} \frac{l_{F}}{g}}$$

   (1)

   A mathematical pendulum of length $l_{M}$ has a moment of inertia

   $I_{A}=m l_{M}^{2}$ and so:

   $$T_{M}=2 \pi \sqrt{\frac{m l_{M}^{2}}{m g l_{M}}}=2 \pi \sqrt{\frac{l_{M}}{g}}$$

   (2)

   When we want $T_{F}=T_{M}$, then we need that $l_{M}=\frac{2}{3} l_{F}$. This $l_{M}$ is called the reduced length of the physical pendulum.

2. When the physical pendulum is suspended in a point $B$, such that its remaining length is $l_{M}$, then again the period is the same! (See Figure 3)

   $T=2 \pi \sqrt{\frac{I_{B}}{m g s}}$

   $I_{B}=\frac{1}{12} m l_{F}^{2}+m s^{2}$ $s=l_{M}-\frac{1}{2} l_{F}$

   and with $l_{M}=\frac{2}{3} l_{F}$, and $s=\frac{1}{6} l_{F}$, we find: $I_{B}=\frac{1}{12} m l_{F}^{2}+\frac{1}{36} m l_{F}^{2}=\frac{1}{9} m l_{F}^{2}$.

   Then the period will be: $T=2 \pi \sqrt{\frac{\frac{1}{9} m l_{F}^{2}}{\frac{1}{6} m g l_{F}}}=2 \pi \sqrt{\frac{2}{3} \frac{l_{F}}{g}}$

   So this pendulum has the same reduced length and the same period as the physical pendulum shown in the first presentation.

3. Between the suspension of $A$ and $B$ the presentation shows that a minimum period appears (suspension at D; see Diagram).

   Now: $T=2 \pi \sqrt{\frac{I_{D}}{m g s}}$ (D being some point at $s$ away from C.)

   $I_{d}=I_{c}+m s^{2}$ and with $I_{c}=\frac{1}{12} m l_{F}^{2}$ we find:

   $T=2 \pi \sqrt{\frac{\frac{1}{12} m l_{F}^{2}+m s^{2}}{m g s}}=\sqrt{\frac{2 \pi}{\sqrt{g}} \sqrt{\frac{l_{F}}{12 s}+1}}$

   $T$ being a minimum for $\frac{d T}{d s}=0$, we find: $s=\frac{l_{F}}{\sqrt{12}}$.

   The length of the stick ( $l_{F}$ ) is 1 meter, so $s$ equals $\frac{1}{\sqrt{12}}=0.289$ meters.

Remarks¶

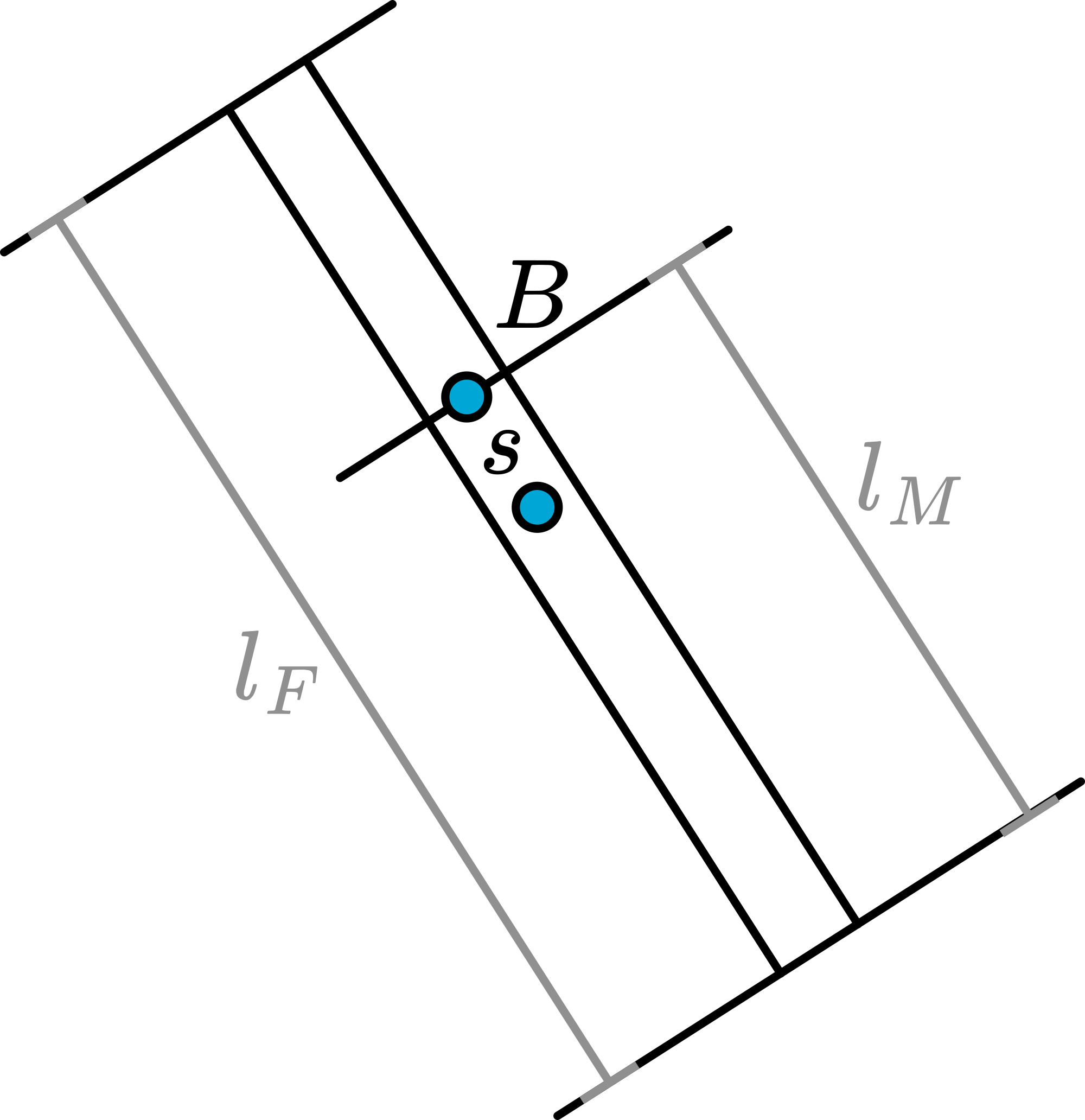
• In order to give the physical pendulum a length of 1 meter and yet have a hole at the ends of this stick, we have triangularly shaped the ends (see Figure 4).

• The differences in $T$ are small. With $I_{F}=1$ meter, we find: $T_{A}\left(=T_{B}\right)=1.64$ sec. And $T_{D}=1.52 \mathrm{sec}$.

  To obtain larger $T$ s a suspension closer to $\mathrm{C}$ is needed.

  Calculating: at $s=12.5 \mathrm{~cm}\left(1 / 8 l_{F}\right), T=1.78 \mathrm{sec}$.;

  at $s=8.3 \mathrm{~cm},\left(1 / 12 l_{F}\right), T=2.09 \mathrm{sec}$;

  $s=2.0 \mathrm{~cm}, T=4.1 \mathrm{sec}$;

  $s=1.0 \mathrm{~cm}, T=5.8 \mathrm{sec}$.

  Of course at $s=0, T=$ infinitive.

• $T=2 \pi \sqrt{\frac{I_{A}}{m g s}}$ shows that physical pendulums of the same mass have

  different periods due to their $I / s$-ratio. Comparing different pendulums can be done when comparing that ratio.

  For a long uniform stick this reduces to comparing the $I_{F} / s$-ratio

Sources¶

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 154-156 and 161-162

• Meiners, Harry F., Physics demonstration experiments, part I, pag. 277-278

• Roest, R., Inleiding Mechanica, pag. 168-169