03 Simple Harmonic Motion (SHM) (1)

Aim¶

To show that a spring-mass system is a harmonic oscillator.

Subjects¶

• 3A40 (Simple Harmonic Motions)

Diagram¶

Equipment¶

• Spring ($k=45\mathrm{~N/m}$).

• Mass ($1\mathrm{~kg}$).

• Demonstration ruler with sliding marker.

• Position sensor.

• Interface and software.

• Projector to project monitor screen.

Presentation¶

The spring is hung to a hook and loaded with a mass of $1 \mathrm{~kg}$. When the mass is at rest the sliding marker is positioned at the centre of mass (CM) of the $1 \mathrm{~kg}$ mass (see Diagram). Then the mass is set in oscillatory motion and it can be observed that the mass oscillates around the original position of the CM. Finally, it will end at this position (due to damping). When the system still oscillates, it is brought to a stop. Taking the mass in your hand and positioing it above its rest position, makes it clear to the students that the force on the mass is directed towards the marker. The same is done by positioning the mass below the marker.

he data-acquisition system shows a (still empty) graph of position versus time. Shortly, the functioning of the data-acquisition system is explained to the students (For instance, when moving your hand above the position sensor, the distance to the sensor is monitored on the presented position graph).

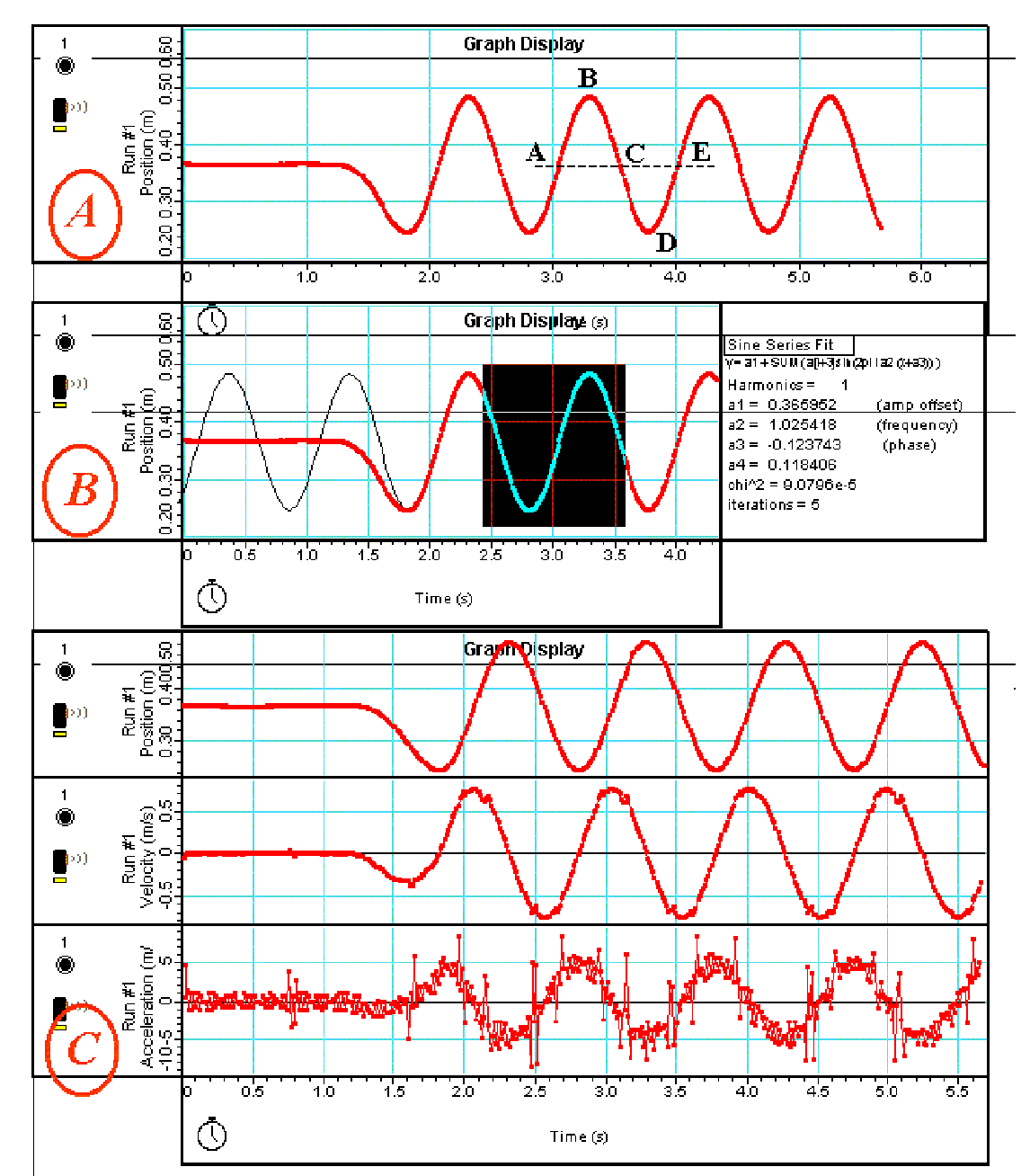
Data-recording is started and the spring-mass system is set in motion again. When about 5 cycles are registered, the data-recording is stopped and the resulting position graph can be studied (see Figure 2A)

1. When the mass rises above the marked rest position the first part ($AB$) of the curve shows that it slows down (because $A B$ becomes more and more level). So during $A B$ the force is downwardly directed. From $B$ to $C$ the graph shows that the mass accelerates (because BC becomes steeper all the time). So also during BC the force is directed downward. CDE can be described in a similar way: always the force is directed towards the rest-position.

2. The graph suggests very strongly that it has a sine-shape. So by means of the software we try a sine-fit (see Figure 2B). This fits very well (very low CHI2- value), confirming our “guess”.

3. Applying the software we add the graphs of velocity and acceleration. The differential relationship between these three quantities can be verified now:

   -The points of zero velocity correspond with maximum - and minimum position;

   -The acceleration-graph is an inverse “copy” of the position-graph;

   -.......

Explanation¶

1. An oscillating system in which the acceleration (or force) is always directed towards a fixed central point and increases linearly with displacement from that fixed point performs a so-called simple harmonic motion. A spring-mass system is such a system: When the (ideal) spring is displaced from its rest position, the restoring force $(F)$ is proportional to this displacement $(F=-k x)$ and directed towards that rest position.

2. Applying Newton’s second law, the dynamic equation of motion is $\frac{d^{2} x}{d t^{2}}=-\frac{k}{m} x$. Solution of this is $x(t)=A \sin \omega t$ The sine-fit in our demonstration confirms this.

Remarks¶

• Making the frequency of the position sensor lower will smoothen the calculated graphs of velocity and acceleration.

Sources¶

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 45-52

• Young, H.D. and Freeman, R.A., University Physics, pag. 394-397