Skip to article frontmatterSkip to article content

01 Magnus Effect (1)

Aim

To show, qualitatively, the lift force on a translating and rotating cylinder.

Subjects

Diagram

.

Figure 1:.

Equipment

Presentation

The first cylinder is placed on the inclined U-profile that is outside the water basin (see Diagram B). It rolls downwards in a way everybody expects. Mark the place where it hits the table.

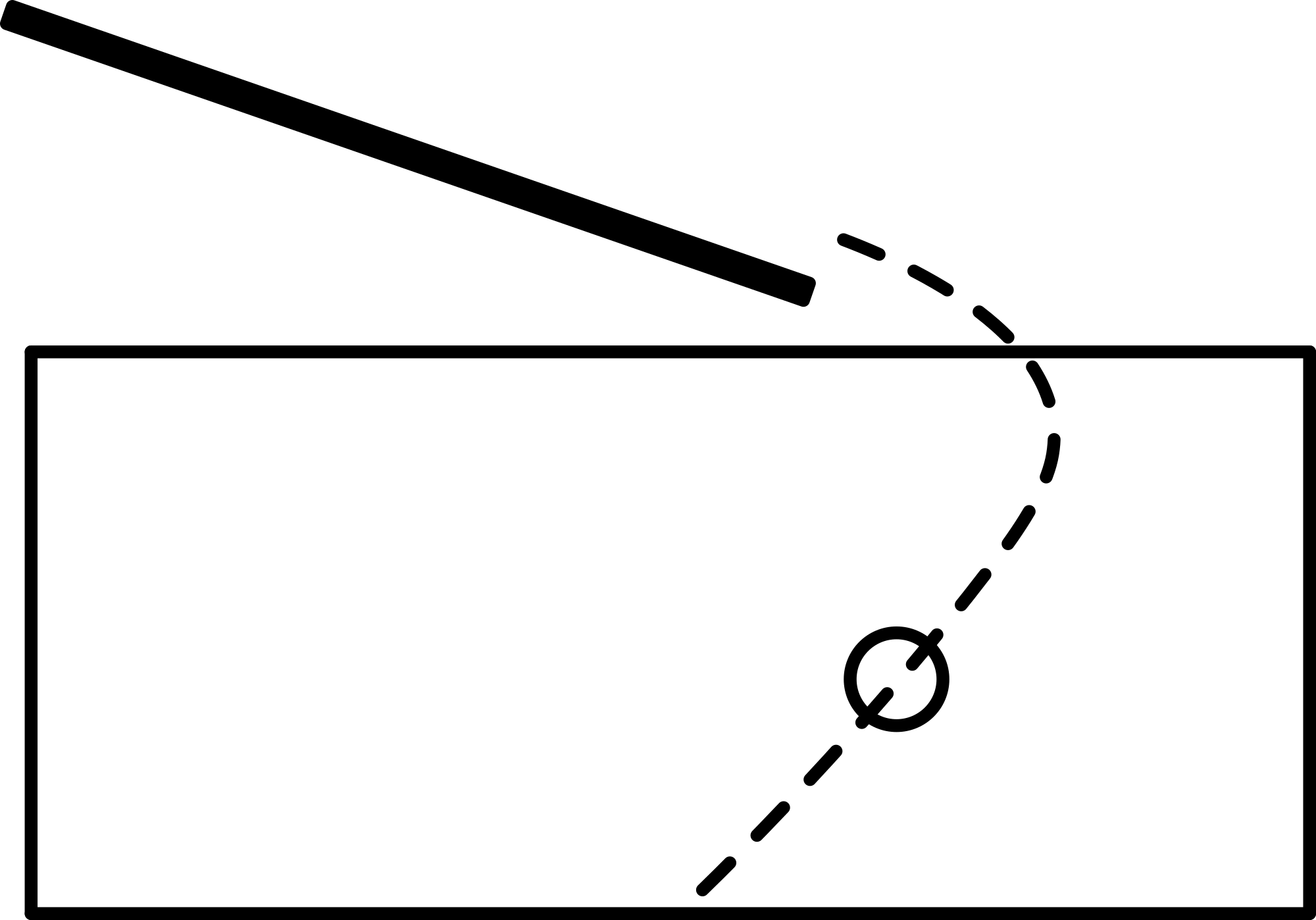
The second cylinder will roll down the inclined U-profile that ends in the water basin. Before doing it, ask the students where this second cylinder will end. (Same way as first cylinder? Or somewhere else?) After their answers this second cylinder is rolled down the incline (see Diagram C) and drops into the water. Instead of following the trajectory of the first cylinder, it moves in a opposite direction (see Figure 2).

.

Figure 2:.

Presentation

The first cylinder is placed on the inclined U-profile that is outside the water basin (see Diagram B). It rolls downwards in a way everybody expects. Mark the place where it hits the table. The second cylinder will roll down the inclined U-profile that ends in the water basin. Before doing it, ask the students where this second cylinder will end. (Same way as first cylinder? Or somewhere else?) After their answers this second cylinder is rolled down the incline (see Diagram C) and drops into the water. Instead of following the trajectory of the first cylinder, it moves in a opposite direction (see Figure 2).

Explanation

A rotating cylinder, moving in a medium (e.g. water) drags that medium round with it. The medium flows in the opposite direction of translation of the cylinder (see Figure 3).

.

Figure 3:.

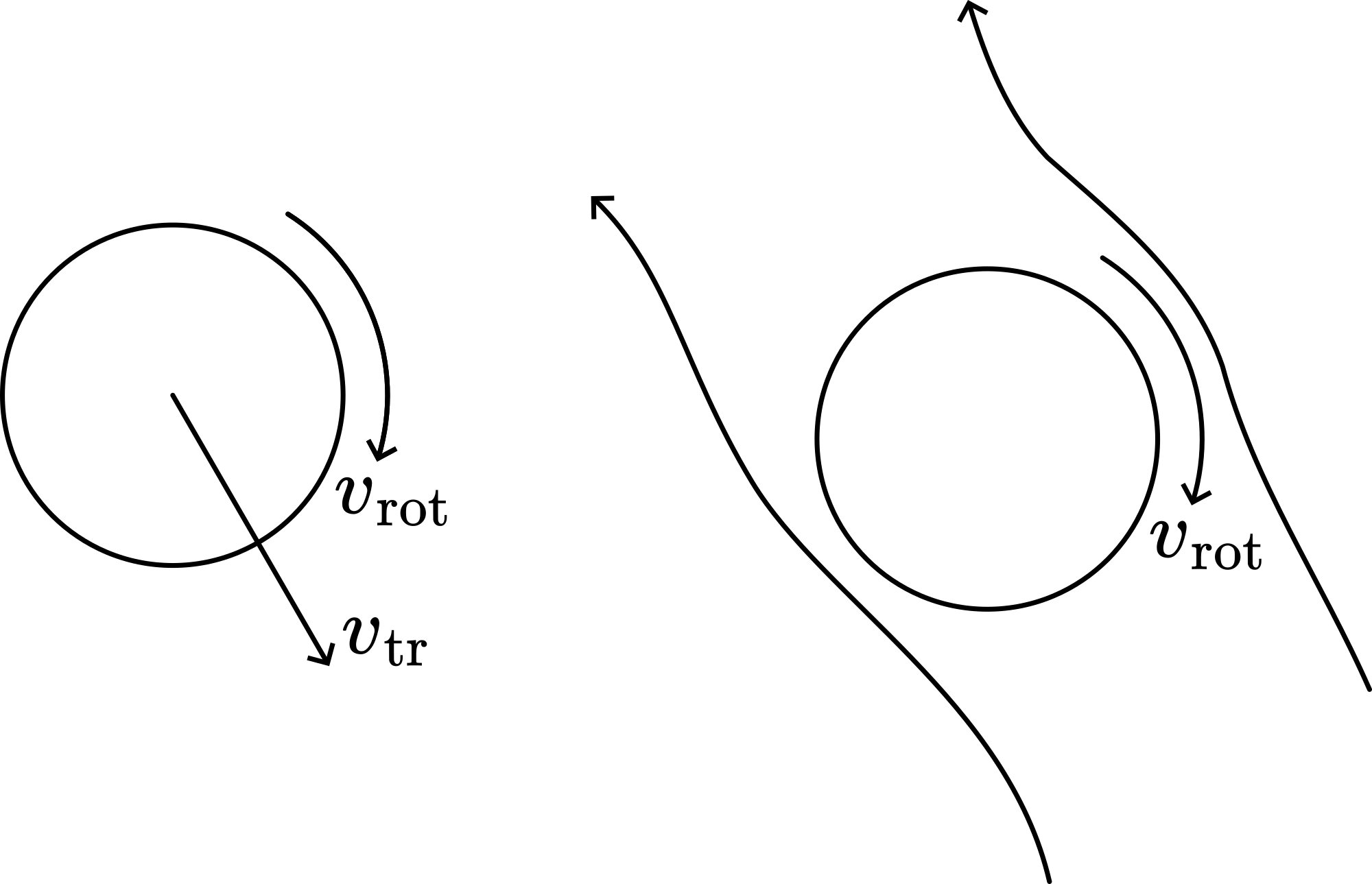
On the right side of the cylinder, the rotation causes the medium to flow slower, while on the other side the medium flows faster. This difference in speed causes a pressure difference; according to Bernoulli’s equation: Δp=12ρ(Vleft 2−Vright 2\Delta p=\frac{1}{2} \rho\left(V_{\text {left }}^{2}-V_{\text {right }}^{2}\right.. Since vleft >Vright v_{\text {left }}>V_{\text {right }}, the net lift-force due to Δp\Delta p is pointing to the left and proportional to ρ(vleft 2−vright 2)\rho\left(v_{\text {left }}^{2}-v_{\text {right }}^{2}\right). Also since vleft =v+ωrv_{\text {left }}=v+\omega r and vriaht =ν−ωrv_{\text {riaht }}=\nu-\omega r, Flift \mathrm{F}_{\text {lift }} is proportional to 2ρωvtr 2 \rho \omega v_{\text {tr }}. Because the density of water equals 103 kg/m310^{3} \mathrm{~kg} / \mathrm{m}^{3}, the lift-force is considerable. Therefore the effect of this force is clearly visible as a deviation of a trajectory without rotation.

Remarks

Sources

2B20 Static Pressure
01 Rotating Liquid
2C20 Bernoulli Force
02 Magnus Effect (2)