02 Magnus Effect (2)

Aim¶

To show, qualitatively, the lift force on a translating and rotating cylinder.

Subjects¶

• 2C20 (Bernoulli Force)

Diagram¶

Equipment¶

• light cylinder, constructed of paper (see diagram)

• 1 meter of wide cloth tape, fixed to a stick

Presentation¶

The cloth tape is wrapped around the middle of the cylinder. The cylinder is laid on a table or on the ground, so that the tape will unwind from the bottom. The stick is pulled giving the cylinder linear and spin velocity. The cylinder lifts itself and describes a loop (see Figure 2).

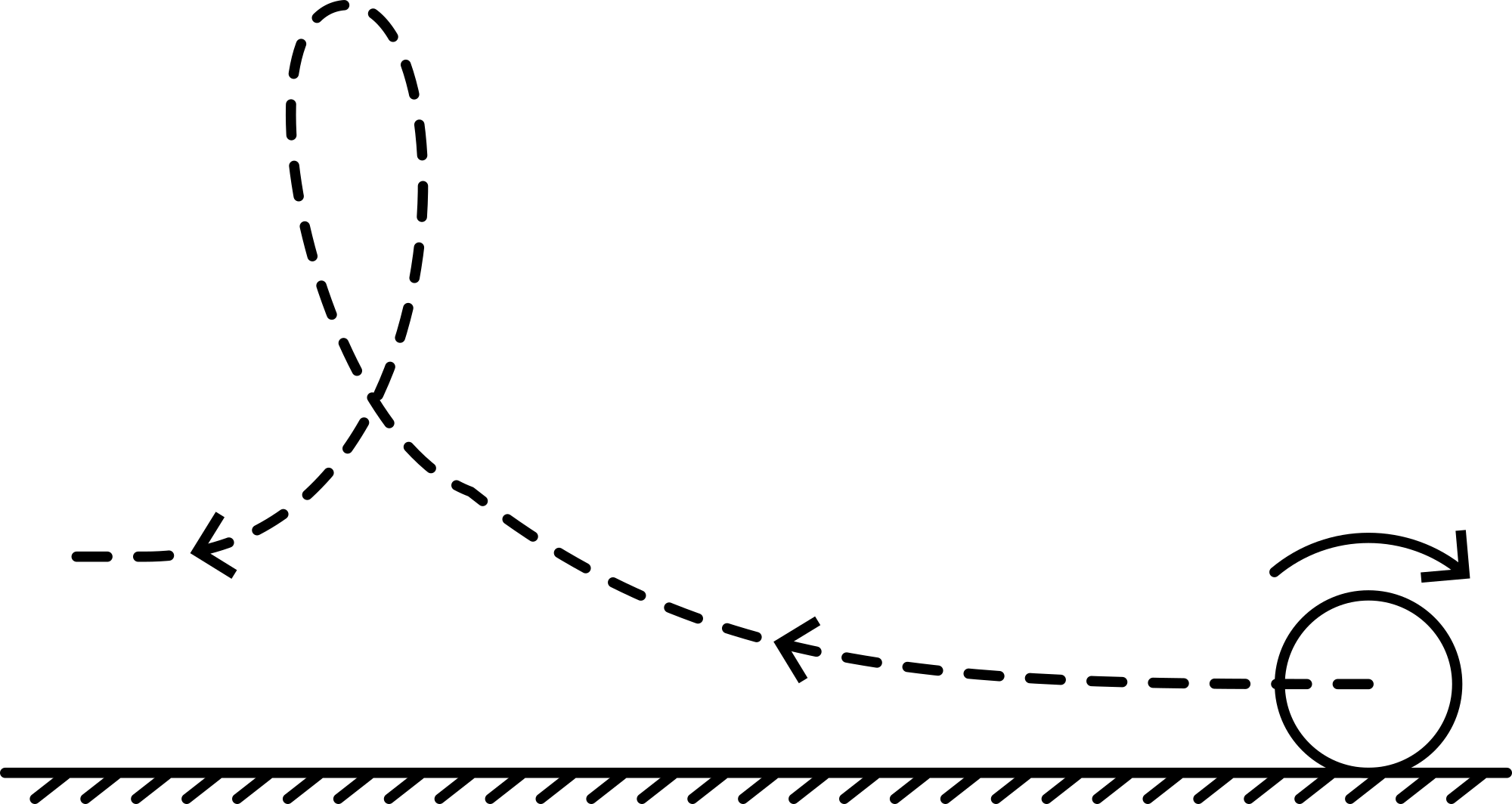
Explanation¶

The rotating cylinder drags the air round with it. The air flows in the opposite direction of translation of the cylinder. On the topside of the cylinder, the rotation causes the air to flow faster, while on the bottom side the air flows slower. This difference in speed causes a pressure difference; according to Bernoulli’s equation: $\Delta p=1 / 2 \rho\left(V_{\text {top }}^{2}-v^{2}\right.$ bottom $)$. Since $v_{\text {top }}>v_{\text {bottom, }}$ the net liftforce is pointing upward and proportional to $20 \omega r v_{t r}$ (see Magnus effect. Since $v_{t r}$ slows down in the beginning of the movement, the cylinder climbs more and more in a vertical trajectory; then it falls down and thus speeding up it moves more and more horizontal: a loop-like trajectory is made by the moving cylinder.

Remarks¶

• In the middle of the cylinder a light piece of wood is stuck to it. Under this piece of wood the cloth tape can be fixed when wrapping it around the cylinder (see Figure 3). When the tape is pulled, the end loosens itself easily from the cylinder.

Sources¶

• Edge, String & sticky tape experiments, pag. 3.12

• Freier, George D. and Anderson, Frances J., A demonstration handbook for physics, pag. F15; F17

• Grimsehl, Lehrbuch der Physik, part 1, pag. 288-291

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 240

• Sutton, Richard Manliffe, Demonstration experiments in Physics, pag. 117

• Vogel, H, Physik, pag. 98-99