01 Going Round in Circles - The Demonstration Laboratory

Aim¶

To see/feel the centripetal force.

Subjects¶

1D50 Central Forces

Diagram¶

Equipment¶

Tube, with rounded edges, $l=15 \mathrm{~cm}$ .
Piece of rope, $l=1.5 \mathrm{~m}$ .
Two rubber stoppers $\left(m_{1}\right)$ .
A number of weights $\left(m_{2}\right)$ . We use thick washers.
Paperclip.
(Stopwatch).

Presentation¶

The diagram shows the components and how to use them. By swinging the tube slightly, the mass $m_{1}$ begins to move in circles above your head. The demonstrator must swing $m_{1}$ at a specific frequency to balance the system.

When the demonstrator slows down to a lower frequency, $m_2$ moves downward, causing $m_1$ ’s circular path to become smaller and smaller. Speeding up causes $m_2$ to rise, and
$m_1$
(1)
moves in increasingly larger circles.
The demonstrator first swings $m_1$ in a stable circular motion. Then, by pulling $m_2$ downward, $m_1$ speeds up dramatically, tracing tighter and tighter circles.

If time permits, the relationship between the variables in this demonstration can be verified more exactly. Just below the tubing, a paperclip is fixed to the rope used as a marker to make $m_{1}$ go round in a circle with fixed $R$ . A stopwatch can be used to time the frequency.

When $m_1$ is doubled by adding another rubber stopper to it, a lower frequency is needed to balance the system.
When $m_{2}$ is increased, a higher frequency is needed to balance the system.
When half the rope length is used (shifting the paperclip), a higher frequency is needed to balance the system.

Explanation¶

Analysis shows that movement at a constant speed ( $v$ ) of a mass ( $m_{1}$ ) in a circle with radius $R$ can be described by $a_{c}=\frac{v^{2}}{r} \omega^{2} R$ . In our demonstration the tension ( $T$ ) in the string provides the force needed for $a_{c}: T=m_{1} a_{c}$ , and $m_{2} g=m_{1} a_{c} \Rightarrow a_{c}=\frac{m_{2}}{m_{1}} g$ , (see Figure 3).

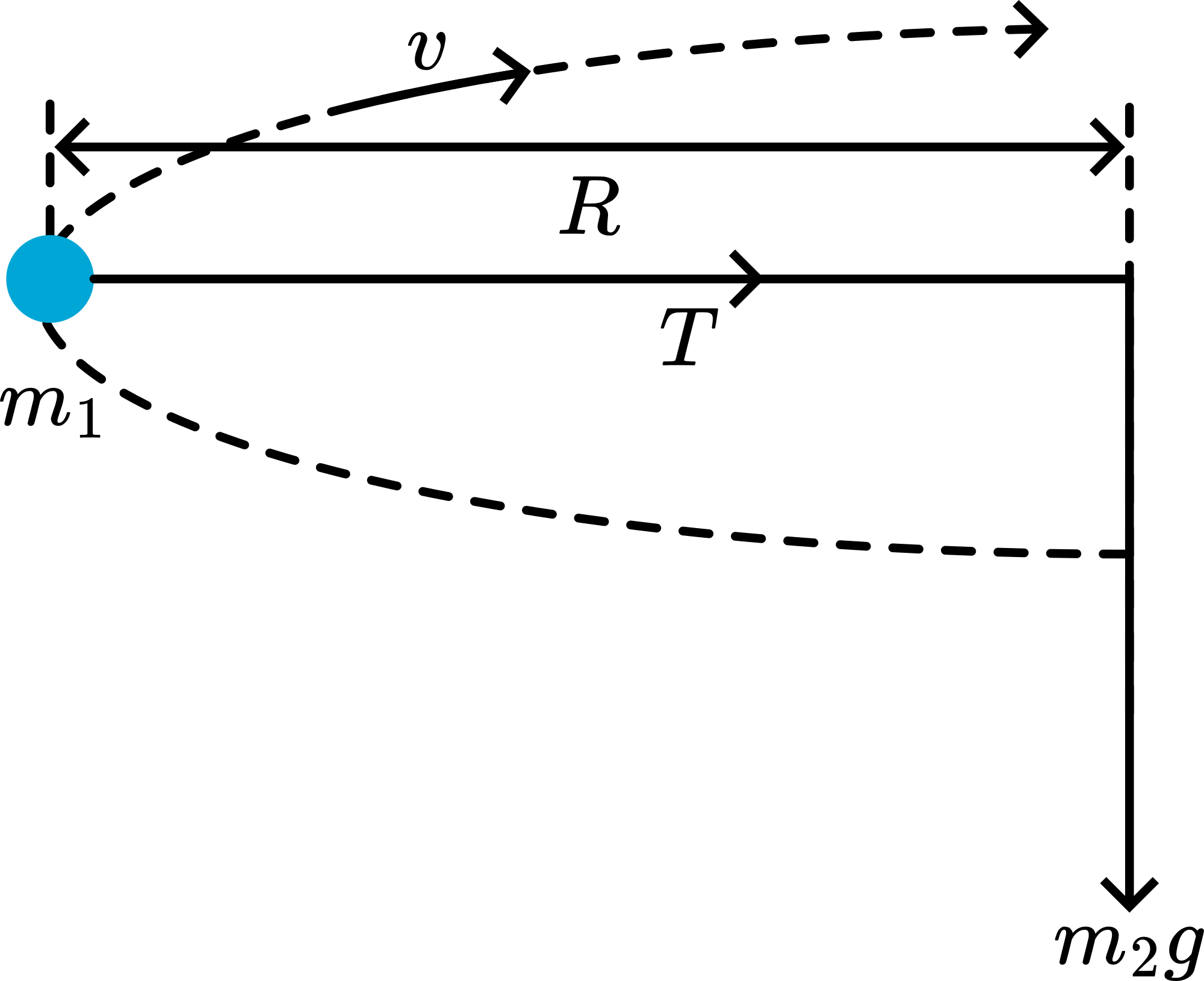
First, the demonstrator showed a balanced situation, after which he slowed down $\omega$ . The centripetal acceleration, describing such a slower movement, will be lower $\left(a_{c}=\omega^{2} R\right)$ . But $T$ is a fixed value, so $T$ will pull $m_{1}$ inwardly. As $a_{c}=\omega^{2} R$ shows, this proces is cumulative and $m_{1}$ ends at the centre of the circle.
When $m_2$ is pulled downward, the string tension increases substantially, and so does $a_c$ . According to $a_c = \omega^2 R$ , and given that $R$ decreases, $\omega$ increases significantly.

Doubling $m_1$ means that the centripetal acceleration $a_c$ provided by the string tension will be halved $\left(a_c = \frac{m_2}{m_1} g\right)$ . To keep $m_1$ moving in the same circle, $\omega$ must decrease by a factor of $\sqrt{2}$ according to $\left(a_c = \omega^2 R\right)$ .
Increasing $m_2$ raises the string tension, so the provided $a_c$ increases $\left(T = m_1 a_c\right)$ . To keep $m_1$ moving in the same circle, $\omega$ has to increase.
When $R$ is halved but the tension in the string remains the same, the provided $a_c$ also remains constant. To keep $m_1$ moving in a (smaller) circle, $\omega$ must increase by a factor of $\sqrt{2}$ according to $\left(a_c = \omega^2 R\right)$ .

Remarks¶

Practice the demonstration before you show it. A practiced hand is needed to make $m_1$ go round properly.
Rubber stoppers are used as masses moving in circles for safety reasons.
The spinning mass should be light compared to the hanging weight (about a factor of 3), because otherwise the angle between the string and the vertical will not approach $90^\circ$ . This leads to more friction, and due to the slanting rope (forming a cone around the circle), the analysis changes.
In the last part of the presentation (grabbing and pulling $m_2$ downward), the demonstrator will feel that quite a lot of force is needed. It is, of course, most instructive for the students if they experience this force themselves (perhaps during the coffee break?).

Sources¶

Ehrlich, Robert, Turning the World Inside Out and 174 Other Simple Physics Demonstrations, pag. 72-73
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 68-71 and74-75