Aim¶
To show that the period of motion of a conical pendulum changes only noticeably at large angles.
Subjects¶
1D50 (Central Forces)
Diagram¶

Equipment¶
Ball suspended on a thread.
Clamping material.
Large paper circle, .
Small paper circle, .
Stopwatch with large display.
A small ball suspended on a thread
Presentation¶
Set up the conical pendulum as shown in the diagram. Place the small paper circle under the pendulum and make the pendulum swing conically along the circumference of the paper circle. Measure the time needed for 10 periods. Repeat this procedure, but now with the large paper circle. In our setup, the times measured are 18.2 and 17.5 seconds, respectively.
Take the small simple pendulum by hand and make it swing conically. Gradually increase its speed. At very large angles, the increase in angular velocity becomes easily noticeable.
Explanation¶
Theory tells us that the period ( ) of a conical pendulum is given by (see Figure 2).
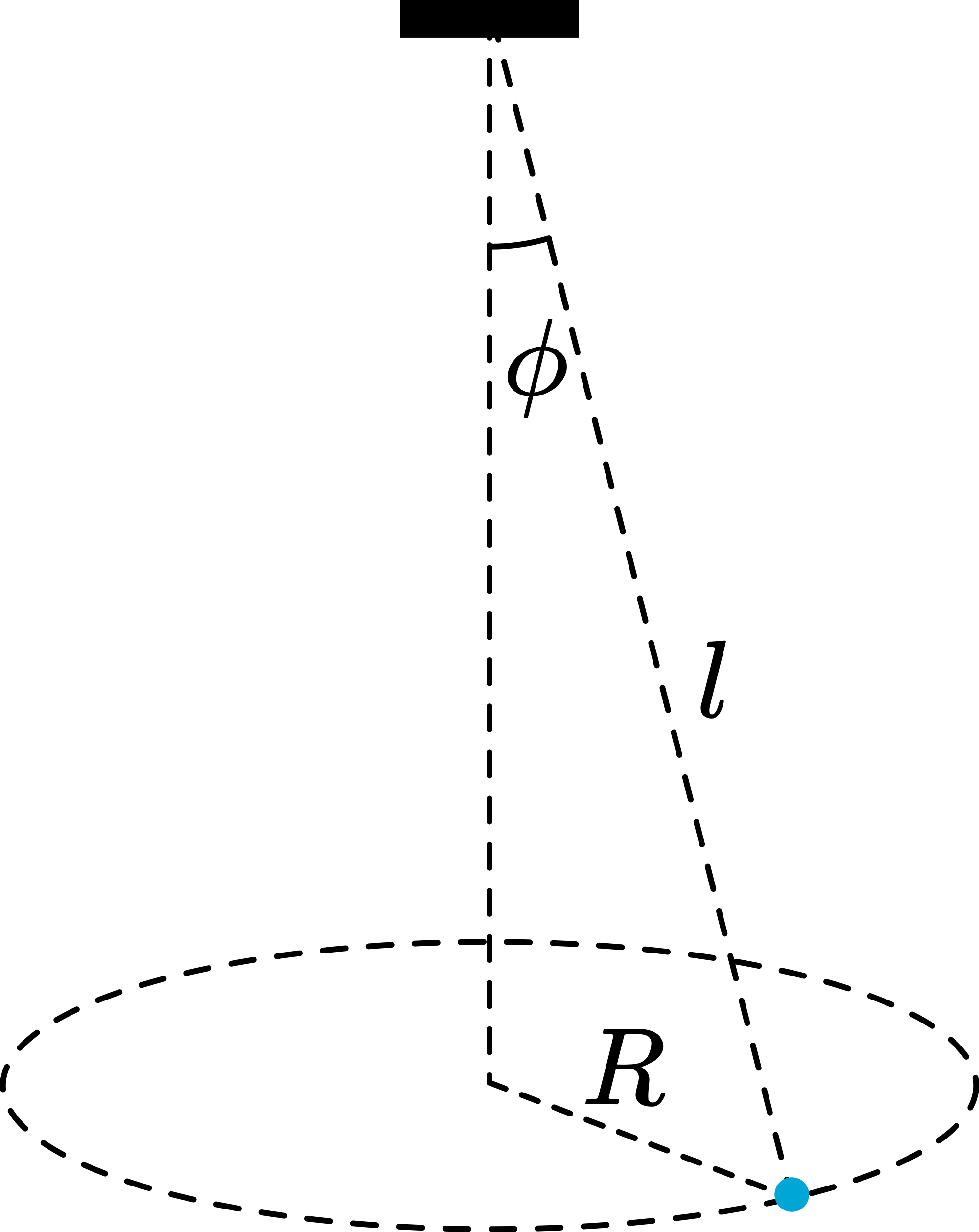
So
The table in Table 1 shows that from to only changes , while from to this change is about . So only at large angles , changes noticeably.
Table 1:table
| 0 | 1 |
| 15 | 0,98 |
| 30 | 0,93 |
| 45 | 0,84 |
| 60 | 0,71 |
| 75 | 0,51 |
| 80 | 0,42 |
| 85 | 0,30 |
| 89 | 0,13 |
Remarks¶
When the pendulum is suspended vertically and not swinging, we have marked this central position on the table. The paper circles have a hole in their center so that it is easy to position them in the right place (hole and mark coincide).
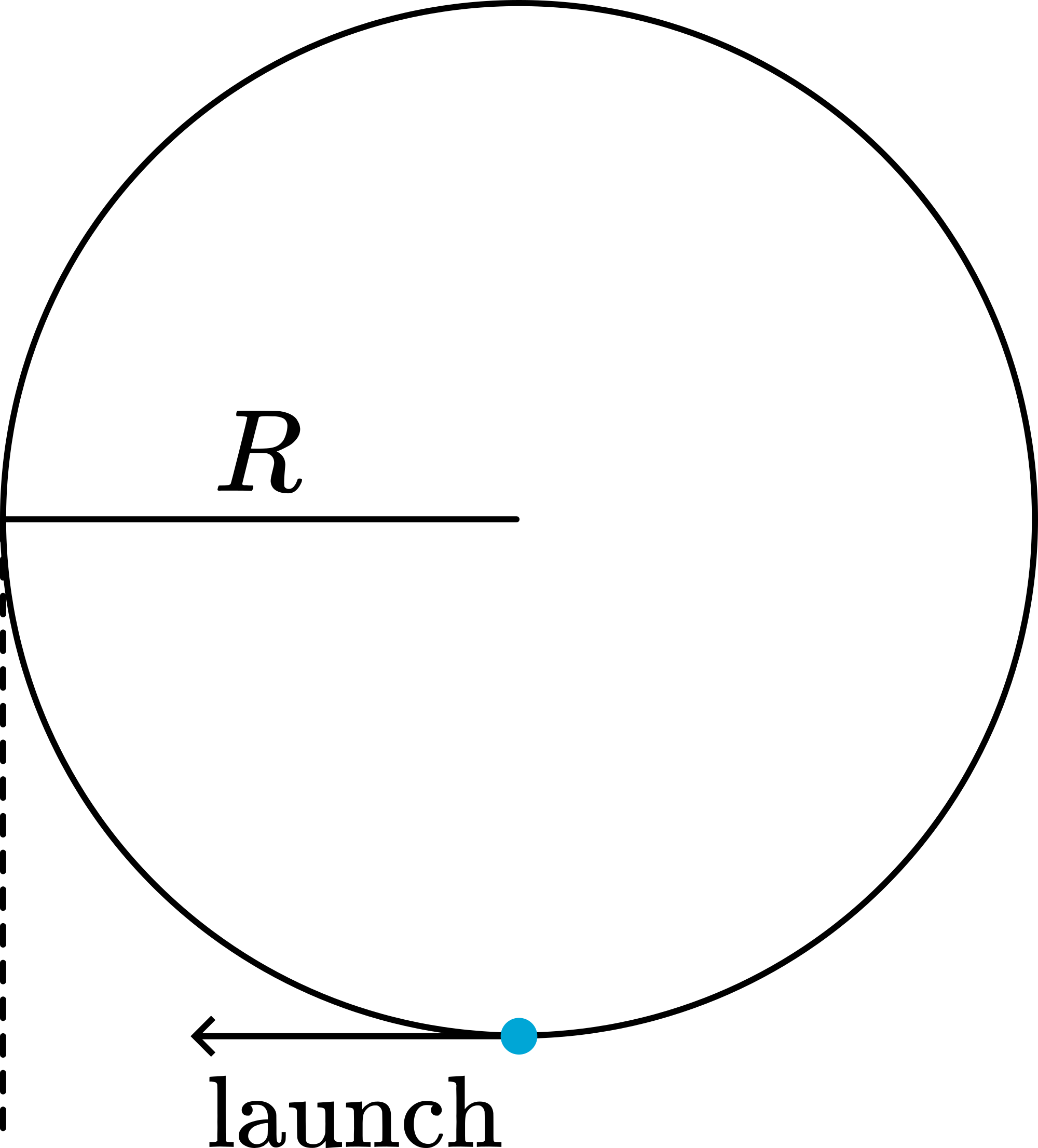
Making the pendulum swing along the circumference of the paper circle needs some practice. Launch the suspended ball tangentially and give it a speed so that it just reaches a deflection equal to of the paper circle (see Figure 3).
Sources¶
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 70
Roest, R., Inleiding Mechanica, pag. 55-56
Young, H.D. and Freedman, R.A., University Physics, pag. 141-142