04 Parallel Wires

Aim¶

To show that parallel wires attract or repel depending on the current direction.

Subjects¶

• 5H40 (Force on Current Wires)

Diagram¶

Equipment¶

• Two long wires, $1.5 \mathrm{~m}$ each

• Power supply (we use $20 \mathrm{~A}$.)

• Amp-meter

• White screen

Presentation¶

The two long wires are suspended from one clamp, close to the rigid white screen. One of the wires is also clamped at the lower end of the white screen and stretched. The second wire is hanging freely in such a way that at the lower end it is about $2 \mathrm{~cm}$ seperated from the fixed wire (see Diagram and Figure 2A).

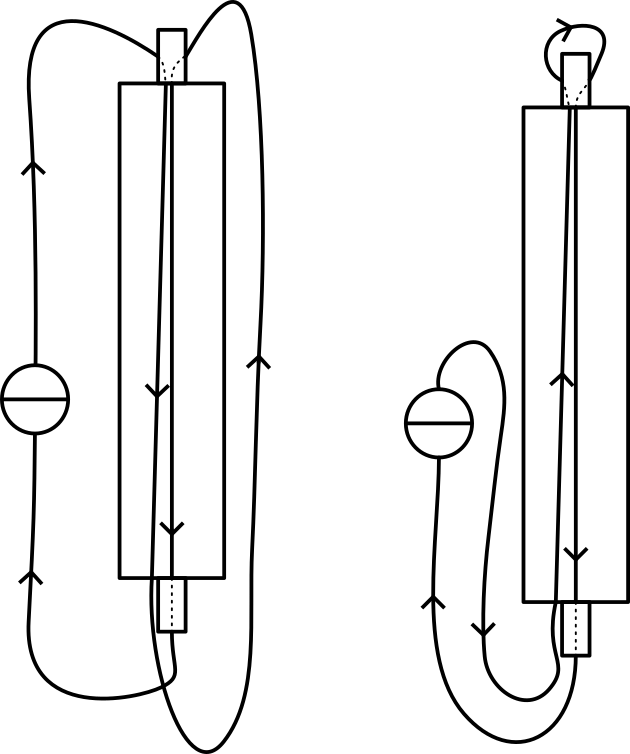
Parallel wires

The wiring is set up in such a way that both wires conduct the current in the same direction (Figure 2A). When switching on the current we see that the “loose” wire moves closer to the fixed wire.

Then the wiring is changed so that the two wires conduct the current in opposite directions (Figure 2B). Switching on the current now shows that the “loose” wire is moving away from the fixed wire.

Explanation¶

The magnetic induction around a current-carrying wire equals: $B(r)=\frac{\mu_{0} I_{1}}{2 \pi r}$ and is directed circularly around that wire (corkscrew). The force on a current in a magnetic field equals $F=I_{2} l B(r)$ and is directed perpendicular to $I_{2}$ and $B . v_{0}$ being $4 \pi .10^{-7} \mathrm{Hm}^{-}$

${ }^{1}$ leads to $F=2.10^{-7} \frac{I_{1} I_{2} l}{r}$.

Applying the rigth-hand rule shows the direction of this force between current $I_{1}(B)$ and $I_{2}$ (see Figure 3).

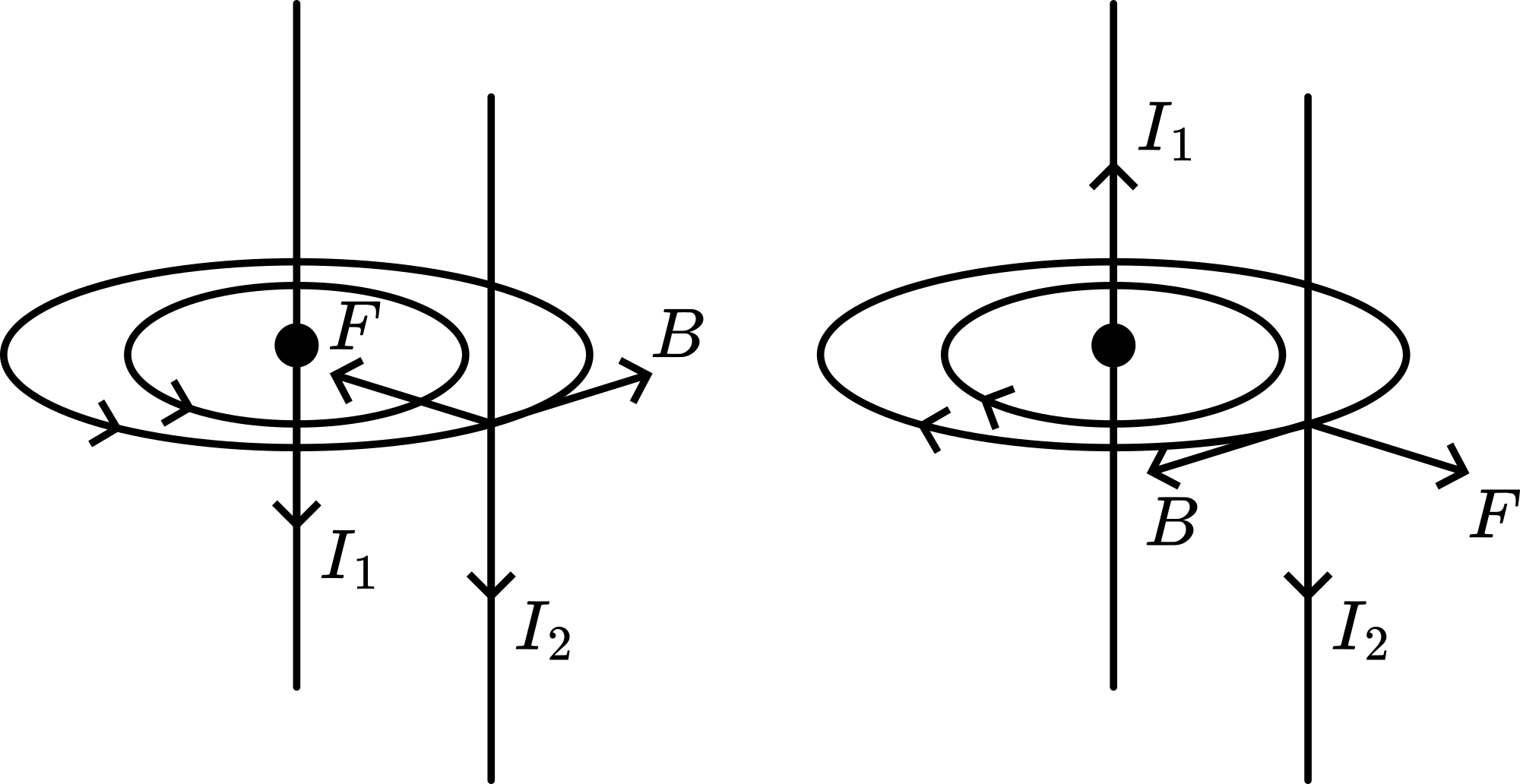
Calculating $\mathrm{F}$ for every $1 \mathrm{~cm}$ length of wire we find:

• at the top where the wires are separated about $3 \mathrm{~mm}: \mathrm{F}=27.10^{-5} \mathrm{~N} / \mathrm{cm}$

• at the bottom where the wires are separated about $2 \mathrm{~cm}: \mathrm{F}=4.10^{-5} \mathrm{~N} / \mathrm{cm}$

• and for the total length of wire: $F=23 \mathrm{mN}$.

So, in this demonstration the force on the wires is very small.

Remarks¶

• When the effect in this demonstration is not visible enough, a video-camera with projection can be used.

• A higher current is advisable for this demonstration; the current shows itself squared in $F$.

• This demonstration can be used in combination with the current-balance demonstration.

Sources¶

• Biezeveld, H. and Mathot, L., Scoop, Natuurkunde voor de bovenbouw, part 4/5 vwo, pag. 223

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 409-410 and 486-487