01 Current Loop in Magnetic Field

Aim¶

To show torques and forces on a current loop in a magnetic field.

Subjects¶

• 5H50 (Torques on Coils)

Diagram¶

Equipment¶

• Two Neodymium magnets fixed in clamps.

• Coil $\left(n=500 ; I_{\max }=2.5 \mathrm{~A}\right)$ with a piece of red tape at one side. The coil is suspended by thin thread, so it can rotate easily (see Diagram).

• Power supply, $30\mathrm{~V}/10\mathrm{~A}$.

• Switch and Two-way switch.

• Array of compass-needles.

• Paperclip (to show the presence of a magnetic field).

• Camera and screen to show the demo to a large audience.

Safety¶

• The Neodymium magnets are very strong. If these magnets are not handled carefully, there is risk of serious injury. The magnets are fixed in clamps and stored with a thick piece of sheet between them.

-Carefully slide them apart when you use them, to prevent your fingers becoming trapped between them.

-Keep them several meters away from magnetic information carriers.

-Never operate the magnets in explosive environments, since they generate sparks!

Presentation¶

Using the array of compass needles we show that there is a uniform magnetic field between the permanent magnets (see Figure 2).

Close to the magnets the field is strongly divergent/convergent (see Figure 3).

Then the coil is suspended between the two magnets (see Diagram). Connecting the power supply to the coil shows that the coil makes a rotation and lines up with the magnetic field (see Figure 4). There it remains at rest.

Conclusion is that in a homogeneous magnetic field a current carrying coil (a dipole) experiences a torque that lines up that dipole with the field. And in that uniform field there is no net force.

Then the coil is displaced a little from its central position: It attracts itself towards one of the magnets and sticks there (see Figure 5).

Conclusion is that in a non-uniform field there is a net force on a current loop (dipole).

Explanation¶

There are Lorentz-forces on all sides of the coil. The forces on the bottom- and topside of the coil cancel (they only tend to stretch the coil). The two forces on the sides are also equal and opposite but they do generate a torque $\vec{N} . \vec{N}=\vec{m} \times \vec{B}$ ( $\vec{B}$ is the magnetic field and $\vec{A}, \vec{A}$ being the area of the current loop).

When the field is non-uniform, there is a radial component of $\mathrm{B}$ and there will be a net force towards the magnet (see Figure 6).

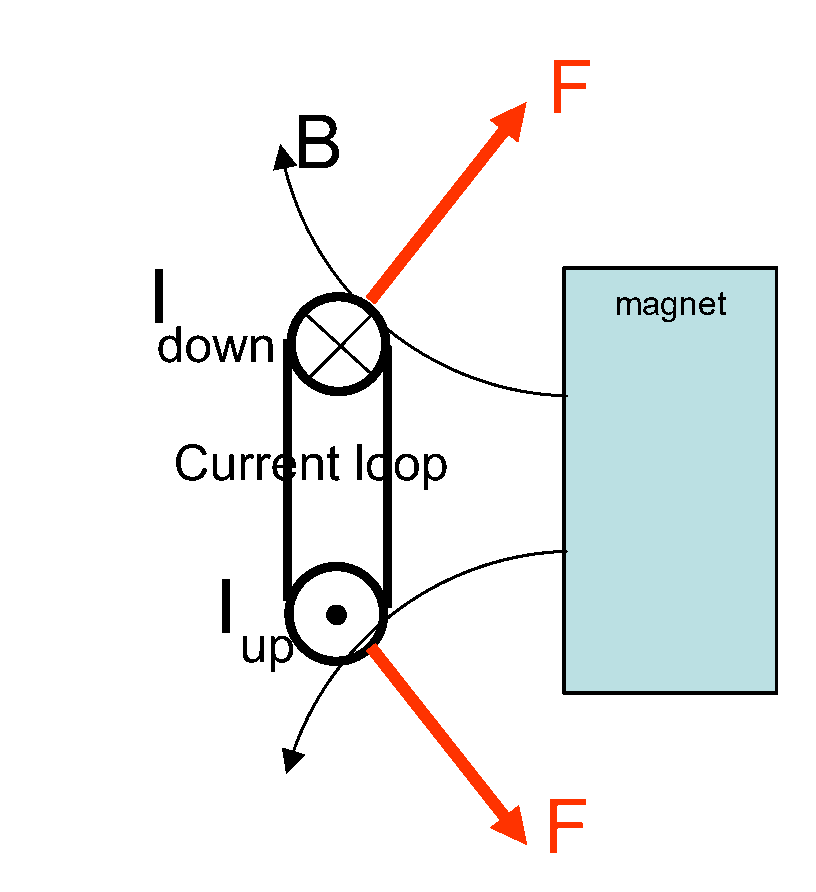
Remarks¶

• The lining up of a current loop in a uniform field is an example of what dipoles do in a material. So it can be used as an example to present para-magnetism.

Sources¶

• Griffiths, D.J., Introduction to Electrodynamics pag.255-258.