01 Self-Inductance in AC Circuit

Aim¶

To show how alternating current depends on the value of self-inductance.

Subjects¶

• 5J10 (Self Inductance) 5L20 (LCR Circuits – AC)

Diagram¶

Equipment¶

• Lamp, $220\mathrm{~V}/200\mathrm{~W}$.

• Coil, $\mathrm{n}=500 ; \mathrm{R}=2.5 \Omega$.

• U-core with bar.

• 2 Demonstration meters.

• Safety connection box .

• Measuring junction box (See Figure 5).

• Net-adapter for mobile telephone (or other appliance).

Safety¶

• It’s a circuit connected to mains voltage ($220\mathrm{~V}/50\mathrm{~Hz}$). That’s why we use a safety connection box. This box shows a green light when the mains is disconnected and a red light when the mains is connected. Self-inductance in AC-circuit

Presentation¶

The circuit is build as shown in Figure 2 and in Diagram. First we show the circuit setup to the students and then connect the two Voltmeters.

1. Connecting the $220 \mathrm{~V}$ to the circuit makes the lamp glows strongly (see Figure 3A ). The Voltmeter connected to the lamp reads almost $220 \mathrm{~V}$ : All voltage appears across the lamp; just a very little voltage is read across the coil.

   Conclusion is that only a very small emf of self-inductance is generated in the coil.

2. The bar is partly shifted on to the U-core. As soon as the bar touches the second leg of the $U$-core the lamp dims (see figure $2 B$ ). the Voltmeter across the lamp shows a lower voltage now and at the same time we observe an increase in voltage across the coil.

   Conclusion is that there is now a higher emf of self-inductance that opposes the $220 \mathrm{~V}$.

3. When the bar is shifted completely on to the U-core, the lamp only glows very faintly. The voltage read across it is very low. The voltage across the coil is almost $220 \mathrm{~V}$ now!

   Conclusion is that the emf of self-inductance generated in the coil is almost $220 \mathrm{~V}$ now.

   Shifting the bar back and forth across the U-core makes the lamp dim less or more.

4. Finally we disconnect the lamp. Now only the self-inductance is connected to the $220 \mathrm{~V}$ (see Figure 4).

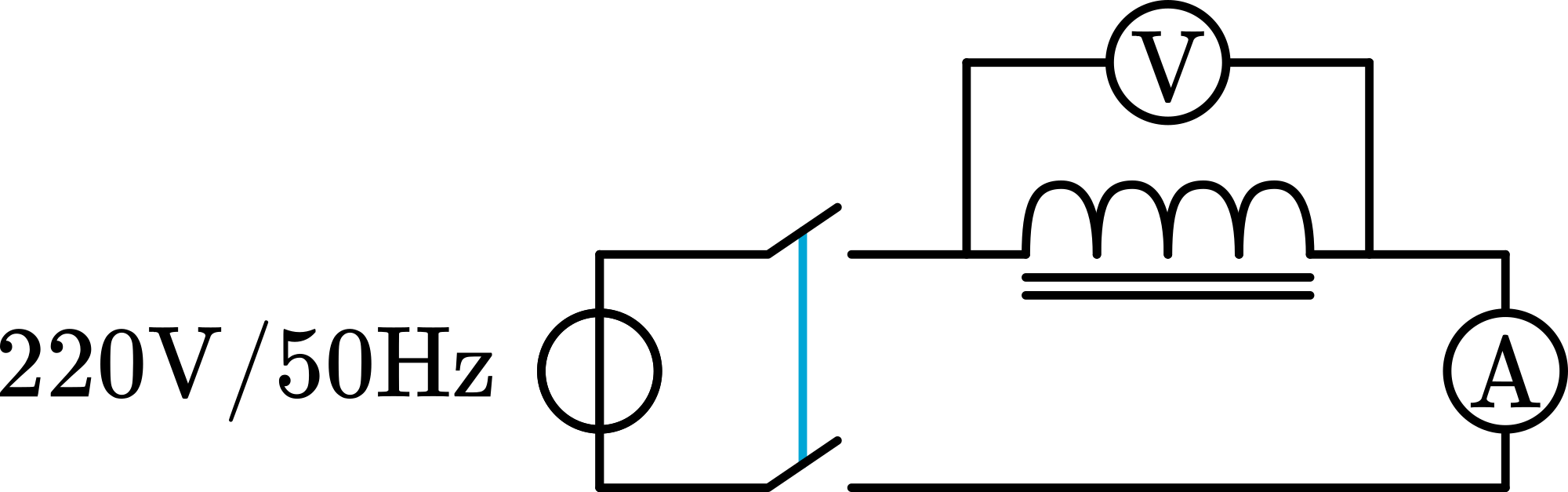
Now the effect of self-inductance is most clear: the voltmeter reads $220 \mathrm{~V}$ across the coil, and only a small current is flowing (we measure $0.4 \mathrm{~A}$ ). When there would be no self-inductance, the current would be $220 \mathrm{~V} / 2.5 \Omega=88 \mathrm{~A}$ !

Conclusion is that the emf of self-inductance really opposes the applied voltage. 5. The same demonstration is performed with a commercial net-adapter (used as charger for a mobile telephone; see Figure 5). Here also only the primary coil of the adapter is connected to the mains. We read a current of only $0.3 \mathrm{~mA}$!

Explanation¶

The emf induced in a coil is, from Faraday’s law: $E=-N \frac{d \Phi_{B}}{d t}=-L \frac{d I}{d t} ; L$ being the coefficient of self-inductance. For a solenoid with a core $\left(\mu_{r}\right)$ this is:

$L=\frac{\mu_{r} \mu_{0} N^{2} A}{l} L=\frac{\mu_{r} \mu_{0} N^{2} A}{l}$. This shows that the higher $L$, the higher the emf of self-inductance. Shifting the bar across the core changes $L$, and so the induced emf.

Remarks¶

• The core on the bar makes a lot of noise. This is a $100 \mathrm{~Hz}$ mains hum due to the mains frequency $(50 \mathrm{~Hz})$.

• The effect of self-inductance can also be translated into impedance of the circuit. In our demonstration 4. the circuit shows an impedance of $220 \mathrm{~V} / 0.4 \mathrm{~A}=550 \Omega$ instead of the $2.5 \Omega$ of the copper coil.

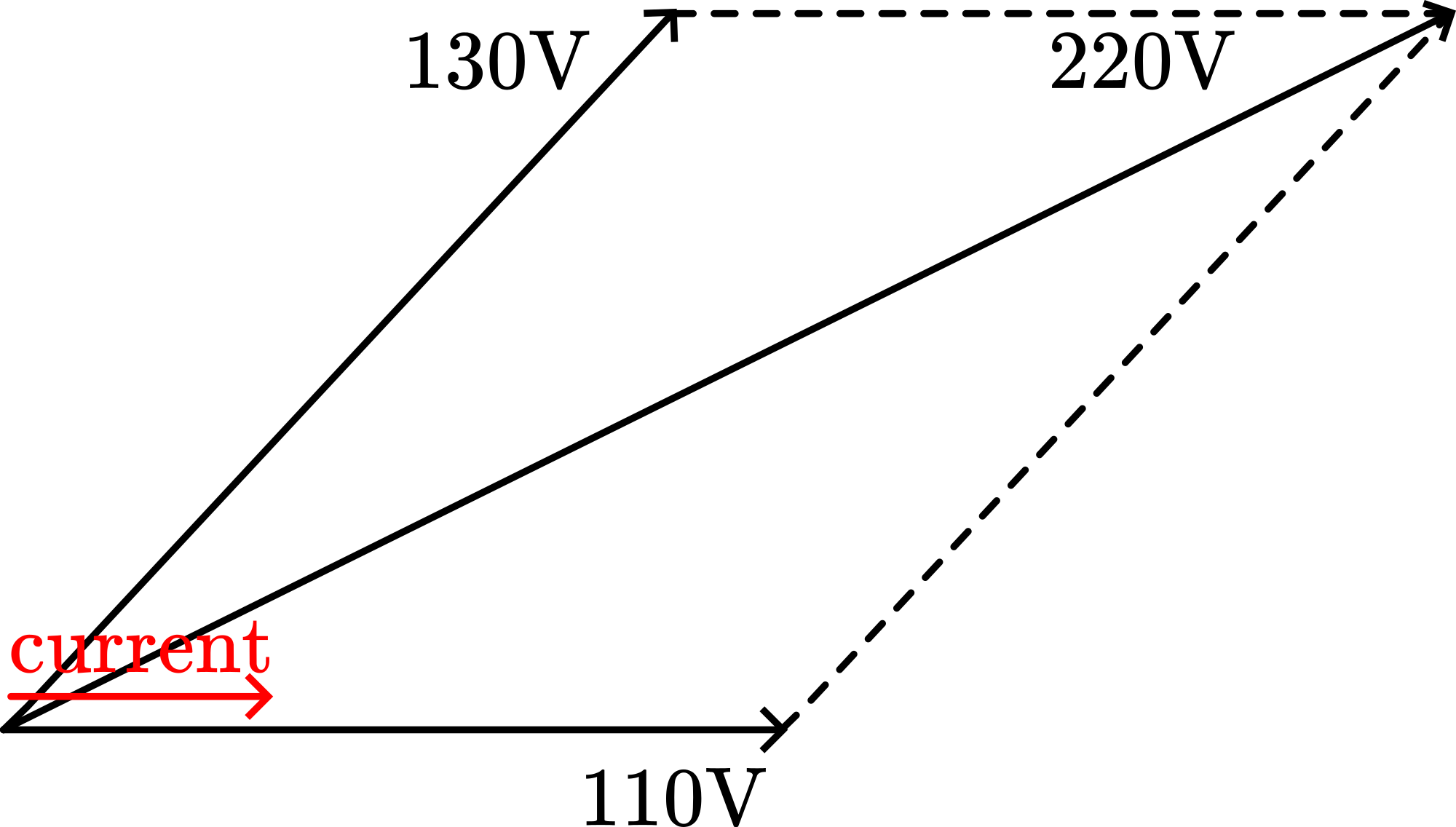
• In figure B we read $V_{\text {coil }}=130 \mathrm{~V}$ and $V_{\text {lamp }}=110 \mathrm{~V}$. Students easily read this as a total of $240 \mathrm{~V}$, so higher than the applied $220 \mathrm{~V}$. Phase-shift between these two voltages is responsible for that. The situation must be something like Figure 6 below shows.

Video Rhett Allain¶

Sources¶

• Giancoli, D.G., Physics for scientists and engineers with modern physics, pag. 758-759 and 773-774.

• Wolfson, R., Essential University Physics, pag. 474-477 and 491-492. 110V