06 Chain Friction

Aim¶

Determining the coefficient of static friction.

Subjects¶

• 1K20 (Friction)

Diagram¶

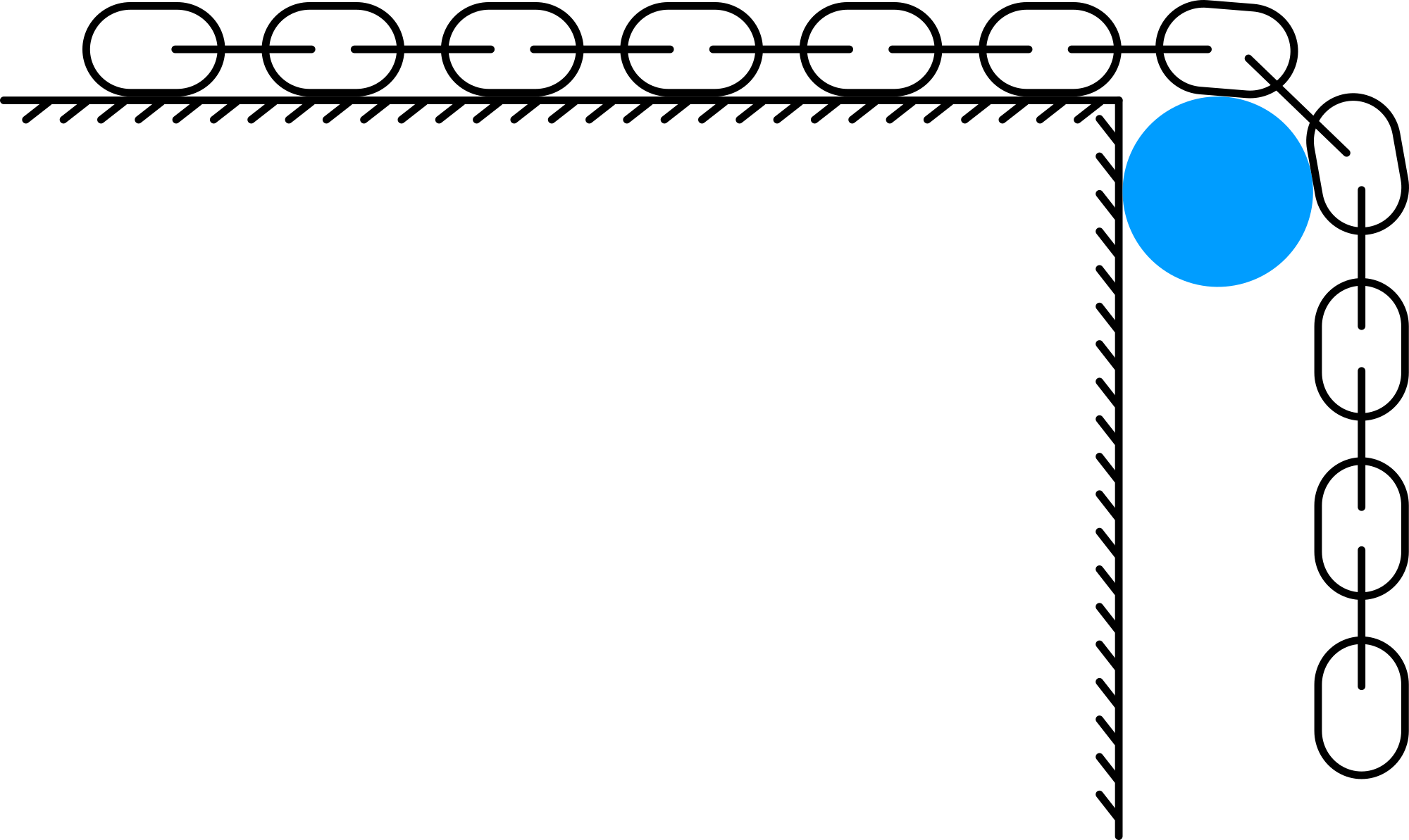
Equipment¶

• Table.

• Chain, ($l = 1.2\mathrm{~m}$).

• Bar.

Presentation¶

The chain is laid out straight on a table. One end is slowly pulled over the edge until the chain just does not slip. The coefficient of friction $\left(\mu_{s}\right)$ between the table top and chain is then $\mu_{s}=\frac{l_{0}}{l-l_{0}}$, where $l$ is the total length of the chain and $l_{0}$ the length of the overhanging portion.

Explanation¶

No slipping means that forces are in equilibrium: $F_{1}=F_{2}$ (see Figure 2).

The mass of the part of the chain hanging over the edge equals: $m_{1}=\frac{l_{0}}{l} m$. This makes: $l_{0} F_{1}=\frac{l_{0}}{l} m g$.

The mass of the part of the chain still on the table equals: $m_{2}=\frac{l-l_{0}}{l} m$.

The normal force of that part of the chain equals: $F_{N}=\frac{l-l_{0}}{l} m g \rightarrow F_{2}=\mu_{\mathrm{s}} F_{N}=\mu_{s} \frac{l-l_{0}}{l} m g$.

$F_{1}=F_{2}$ now yields: $\frac{l_{0}}{l} m g=\mu_{s} \frac{l-l_{0}}{l} m g$, and so: $\mu_{s}=\frac{l_{0}}{l-l_{0}}$.

Remarks¶

• It is advisable to make the corner of the table a low friction surface, e.g. rounding that corner. You can of course also make a special surface for your chain (acrylic plate, bended at one end). We used a stand bar as a low friction surface for the corner of the table.

• Instead of a chain, the demonstration can also be done with a piece of soft cloth or rope.

Sources¶

• Meiners, Harry F., Physics demonstration experiments, part 1, pag. 152