01 Weighing the Earth

Aim¶

To show the experiment of Cavendish.

Subjects¶

• 1L10 (Universal Gravitational Constant)

Diagram¶

Equipment¶

• Computerized Cavendish Balance.

• Data-acquisition system.

• Some models of torsion balances (see Diagram A).

Safety¶

• You are manipulating lead balls in this experiment. So wash your hands after you have performed the demonstration.

Presentation¶

First a short historical survey is presented to the students:

• 1687: Newton’s law on gravitation published in his “Philosophia Naturalis Principia". In this “Principia” he considers that the attraction of a pendulum (that hangs straight downwards) by a mountain could be used as a practical demonstration of his theory (see Figure 2), but pessimistically he thought that any real mountain would produce too small a deflection to measure.

• An experiment to test Newton’s gravitational law would provide an estimate of the mass and density of the Earth. Since, by that time, the masses of astronomical objects were known in terms of relative ratios, the mass of the Earth would provide reasonable values of density and mass to the other planets, their moons, and the Sun.

• 1738: A French team performs plumb-line measurements next to the volcano Chimborazo in Ecuador. They determined a deflection of 8 seconds of arc, but doubted the reliability of their results (they measured in very difficult circumstances).

• 1774: The plumb-line experiment is conducted around the Scottish mountain of Schiehallion. A deflection of 11.6 seconds of arc is measured (the sum of the north - and south deflections). Based on these measurements Hutton determined in 1778 that the earth had a mean density of about 9/5 of that of the mountain, and announced that the mean density of the Earth is $4,500 \mathrm{~kg} / \mathrm{m}^{-3}$. He also gives a density table for the other planets and the Sun.

• 1783: John Michell, a geologist, invents the torsion balance (independent of Coulomb in France) in order to measure the force of gravity between masses in the laboratory. He dies in 1793 before he could begin the experiment. His apparatus was sent to Cavendish who performed and completed the experiment in 1798.

Pictures of Cavendish balance are shown to the students (see Figure 2).

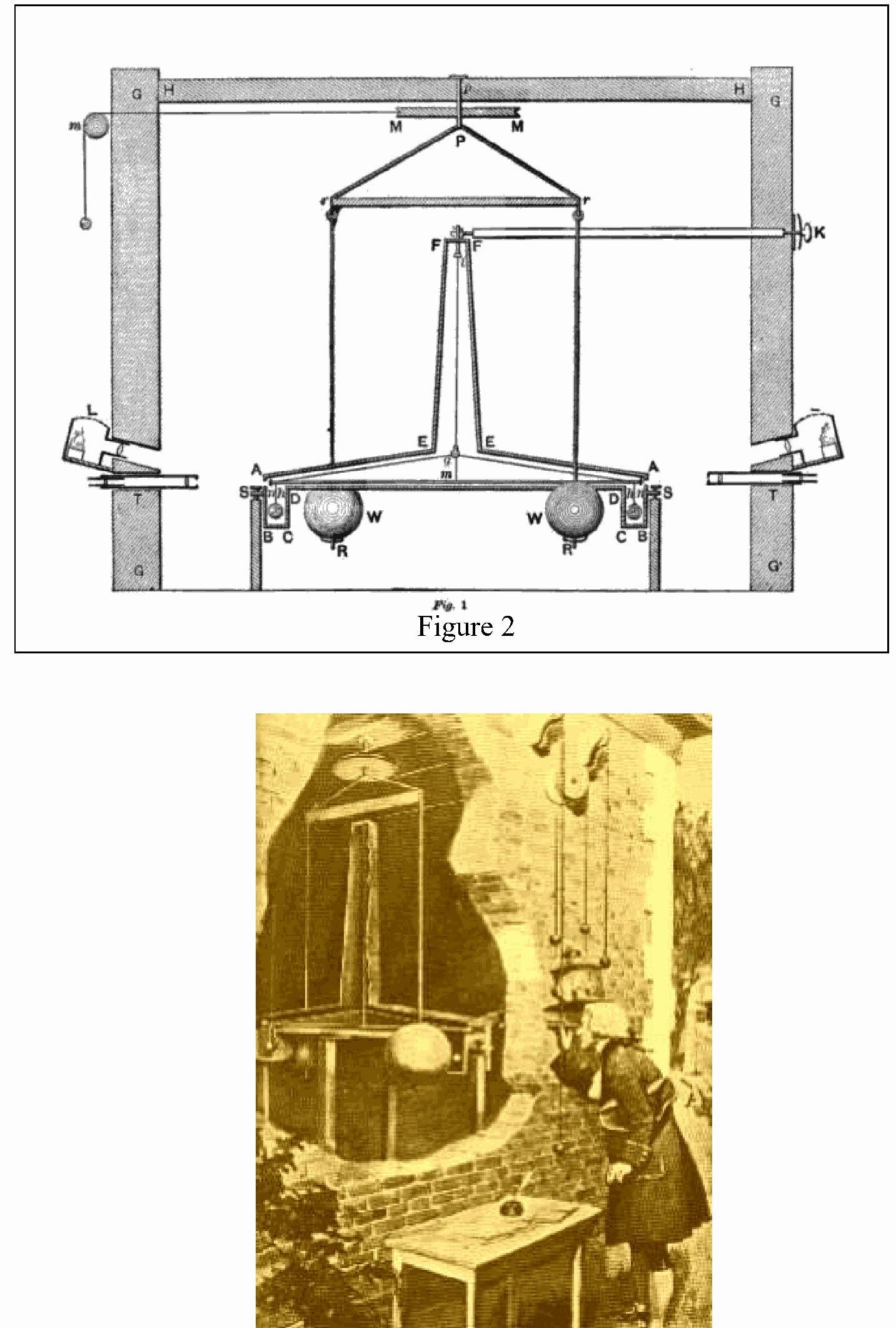
Our instrument (see Diagram B) is explained to the students and compared with Cavendish’s construction:

It is essentially a torsion pendulum in which two small lead balls ( 15 gram each) rest on the ends of a light aluminium boom. This boom is suspended in the centre by a thin tungsten wire (diameter is 25 micron). All this is mounted inside a draft proof case. On the outside of the case two larger lead balls (1 kilogram each) can be swivelled from one side to the other (see Figure 4).

The position of the boom is measured in a capacitive way: the boom is suspended between capacitor plates mounted in the aluminium case. This transducer comprises two sensors to eliminate noise due to vibrations. The transducer output is proportional to the angular movement of the boom. The angular displacement appears on the monitor screen as a function of time (see Figure 5).

At the beginning of the lecture a small displacement of the boom is given (for instance by a little “shock” to the table). It takes quite a long time before the boom is at rest again (see the example in Figure 5, in which it took around 3000 seconds before the boom was damped enough to perform the demonstration). In this damping the students can clearly observe the torsional vibration of the boom.

(Giving the model torsion-balances a small deflection will strengthen their imagination of what is happening inside the casing of our instrument.)

In $\mathrm{P}-\mathrm{Q}$ we swivel the lead balls in the right rhythm from one position to the other in order to drive the boom to higher amplitudes (swivel from one side to the other when the indicated amplitude is at its extreme value). This part shows clearly that there must be an attractive force that is responsible for the increasing amplitude.

Explanation¶

The mountain experiment (see Figure 2):

$F=G \frac{m M_{M}}{d^{2}}$ And $W=G \frac{m M_{E}}{r_{E}^{2}}$. This leads to: $\frac{F}{W}=\frac{M_{M}}{M_{E}}\left(\frac{r_{E}}{d}\right)^{2}=\frac{\rho_{M} V_{M}}{\rho_{E} V_{E}}\left(\frac{r_{E}}{d}\right)^{2}$

$\frac{F}{W}=\tan \theta$, so $\frac{\rho_{M}}{\rho_{E}}=\frac{V_{E}}{V_{M}}\left(\frac{d}{r_{E}}\right)^{2} \tan \theta$.

Since the volumes of the Earth and mountain are known as are $r_{E}$ and $d$, then $\frac{\rho_{M}}{\rho_{E}}$ is determined in measuring the angle of the plumb-line with the vertical. Knowing $\rho_{M}$ (soil drilling), $\rho_{E}$ is determined.

Cavendish experiment:

In order to know the force between the lead balls, the torsion constant of the wire needs to be known. Oscillation experiments yield this value (see manual). Quite a lot of calculation is needed, also for the determination of $G$ out of the oscillations. So this is not suitable when demonstrating. The demonstration just shows that here is an attractive force working.

Once $G$ has been found, the attraction of an object ( $m$ ) at the Earth’s surface to the Earth itself can be used to calculate the Earth’s mass and density:

In this way Cavendish found that the Earth’s density is 5.448 times that of water. (Cavendish was not interested in the value of $\mathrm{G}$. To him was just a proportionality constant, in which he was not specifically interested. To us that is different.)

Remarks¶

• Treat the Cavendish balance carefully, it is a sensitive instrument.

• Fix the table to the floor and be sure it is a massive floor the assembly is standing on (a wooden floor moves too much).

Video Rhett Allain¶