05 Pendulum of Death

Aim¶

To show that we really trust the law of conservation of energy.

Subjects¶

• 1M40 (Conservation of Energy)

Diagram¶

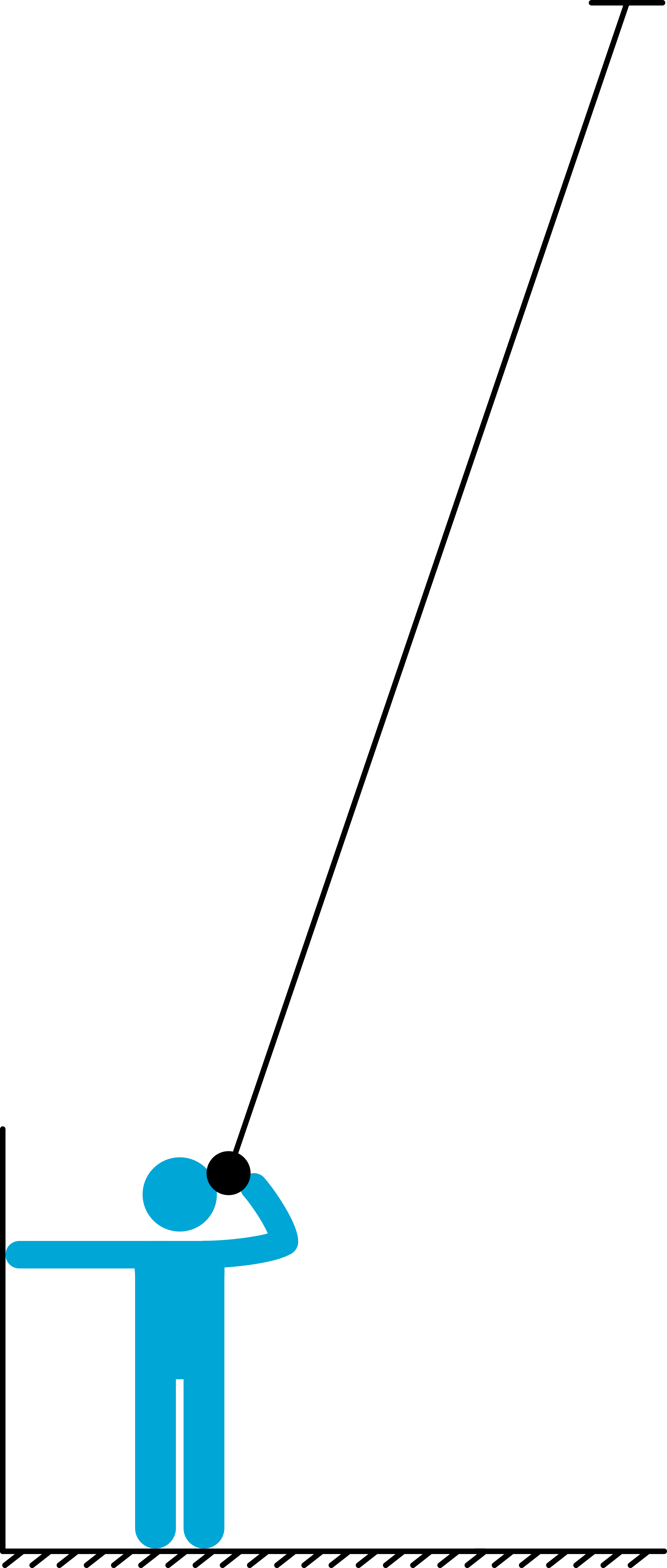
Equipment¶

• Long pendulum suspended from the ceiling of the lecture hall.

• Some kind of support.

Presentation¶

A long pendulum is suspended from the ceiling of the lecturehall. The pendulum bob is a heavy cast-iron sphere. The demonstrator draws the bob to one side and puts his head immediately adjacent to it and steadies himself against some support. Then he releases the ball, and keeping his eyes fixed on the audience, he explains that he is willing to risk his head to demonstrate that the law of conservation of energy applies! Meanwhile, the ball has been swinging far out, and is returning to his head threateningly. But the ball slows down as it regains its original level and barely touches the head. The law of conservation of energy has given a correct prediction: the demonstrator survives.

Explanation¶

Mechanical work done by a field force in moving a body between $A$ and $B$ is defined as: $W_{A B}=\int_{A}^{B} \vec{F} d\vec{s}=U\left(\vec{r}_{A}\right)-U\left(\vec{r}_{B}\right)$, (independent of the path taken: conservative force field). $U(\vec{r})$ is called the potential energy function.

Also can be shown (using $\vec{F}=m \vec{a}$ ) that $\int_{A}^{B} \vec{F} d \vec{s}=\frac{1}{2} m v_{B}^{2}-\frac{1}{2} m v_{A}^{2}=K_{B}-K_{A} . K$ is called: kinetic energy.

Combining these two equations: $U_{A}+K_{A}=U_{B}+K_{B}$.

So the pendulum bob moves in such a way that $U+K=E=$ constant. On release the bob has only potential energy $E=U_{A}$. When it returns to its original height it has the same amount of potential energy, so then $K=0$, and $v=0$. Reaching a point higher than $\mathrm{A}$ should mean that $E$ has to increase, which violates $U+K=E=$ constant.

Remarks¶

• When the demonstrator is not sure about the result of the demonstration he will, just before the final moment, steal a glance at the approaching pendulum, and he will involuntarily recoil! It surely will enlighten the demonstration when the first time you do it in this way.

• When letting the pendulum go be sure not to give it some push. Conservation of energy still applies, but your head will not appreciate this. Be careful.

Video Rhett Allain¶

Sources¶

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 87 and 90-91

• Meiners, Harry F., Physics demonstration experiments, part I, pag. 74 and 179