07 Pulling a Slackened Rope

Aim¶

To show that only a short impulse is needed to make a student move.

Subjects¶

• 1N20 (Conservation of Linear Momentum)

Diagram¶

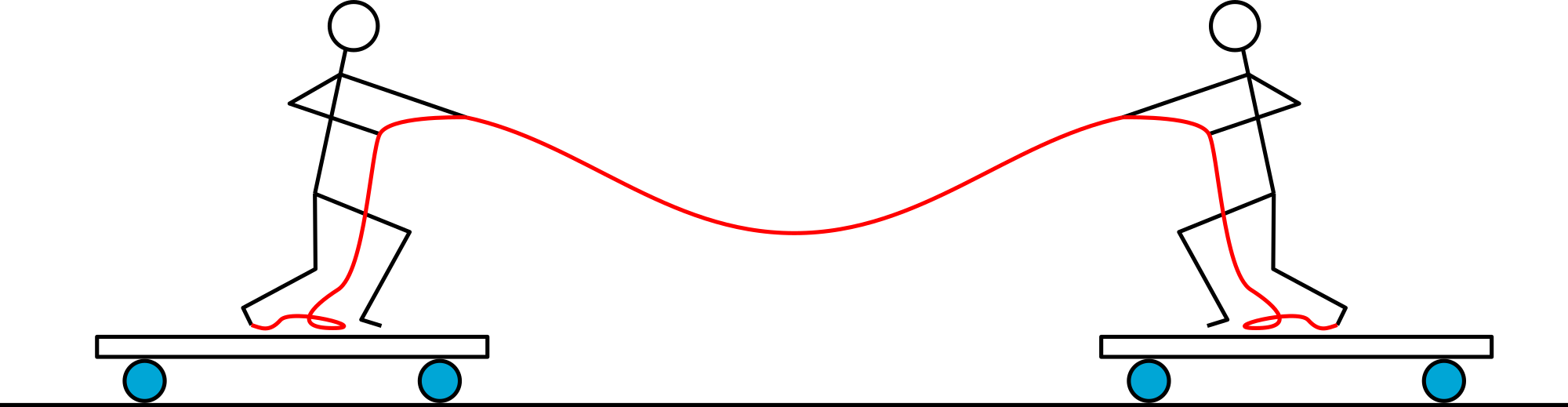
Equipment¶

• Two light carts, easily rolling.

• Rope; $l=10\mathrm{~m}$.

• Two students.

Presentation¶

The two students stand each on a cart. Between them is a slackened rope. Slowly they increase the tension in the rope and at a certain moment both carts start moving towards each other. The rope slackens again, but both carts keep on moving. (Eventually friction will stop their movement.)

When there is a clear mass difference between the two students, the difference in their respective speeds will be clearly observable.

Explanation¶

The tension in the rope implies an impulse $F \Delta t$ to the cart + student. This impulse changes the momentum $p=m_{1} \Delta v_{1}$ of the cart + student. Applying Newton’s second law we can say: $F \Delta t=m_{1} \Delta v_{1}$. When the initial velocity is zero, then $m_{1}$ will move with $v_{1}$ after the short impulse is over.

Applying ‘conservation of linear momentum’ to the whole system it is clear that the change of momentum of $m_{2}$ is $-\Delta p=m_{2} \Delta v_{2}$. $v_{2}$ will be opposite to $v_{1}$ and when $m_{2}>m_{1}$, $v_{2}$ will be lower than $v_{1}$.

Sources¶

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 122-123