04 Precession (2)

Aim¶

To show precession (and to show the validity of vector-addition)

Subjects¶

• 1Q50 (Gyros)

Diagram¶

Equipment¶

• Bicycle-wheel with handles.

• 2 pieces of rope.

• Pair of scissors.

Presentation¶

The wheel is supported by strings tied to both handles. The wheel is given a fast spin by hand. Now one of the supporting strings is cut. The wheel starts to precess about a vertical axis (while its own horizontal axis of spin slowly descends toward the vertical). As the spin of the wheel diminishes, the wheel precesses more rapidly.

Explanation¶

Since angular momentum is a vector quantity that may be conveniently represented by a vector parallel to the axis of spin, the combination of two angular momenta may be treated by the parallelogram law. Thus, whenever a gyroscope is acted upon by a torque tending to produce rotation about an axis perpendicular to the axis of spin, the gyroscope will precess about a third axis perpendicular to the other two.

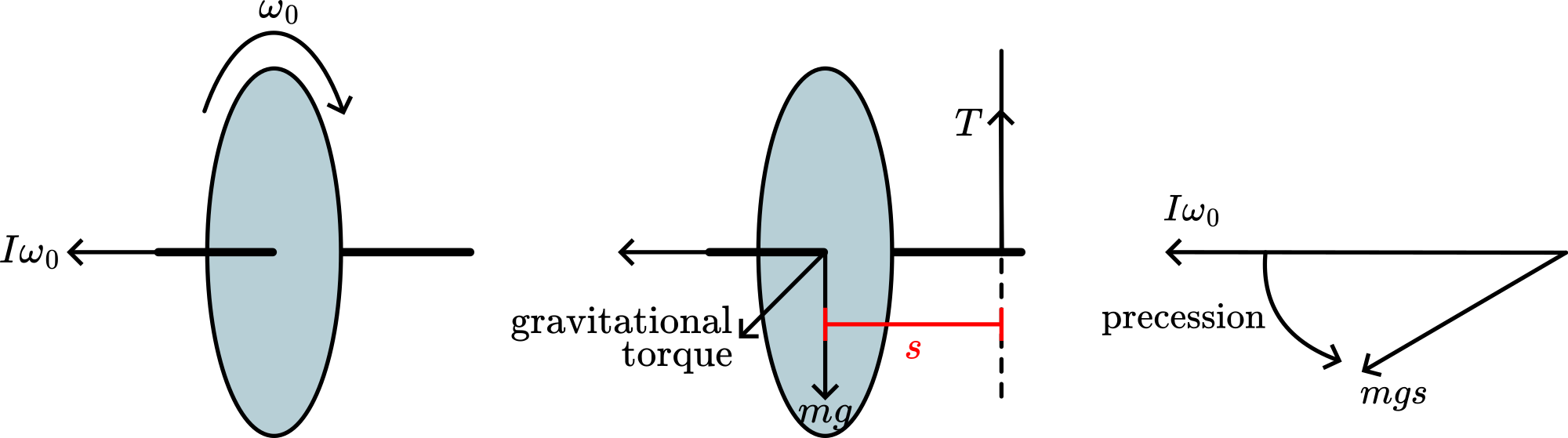
The spinning wheel has an angular momentum of $I \omega_{0}$. This is represented by a vector parallel to the axis of spin (see Figure 2 a). When one of the strings is cut, then gravitational torque ( $\mathrm{mgs}$ ) is added to the system (see Figure 2 b ). This torque tends to change $I \omega_{0}$, so $I \omega_{b}$ moves into the direction of $m g s$ (see Figure 2 c).

It can be shown that the speed of precession $\left(\omega_{p}\right)$ is given by $\omega_{p}=\frac{m g s}{I \omega_{f}}$, so slowing down of $\omega_{0}$ increases $\omega_{0}$. The precession will also be more rapid by adding a weight to the unsupported handle.

Sources¶

• Sutton, Richard Manliffe, Demonstration experiments in Physics, pag. 79