06 Nutation (1)

Aim¶

To show nutation.

Subjects¶

• 1Q50 (Gyros)

Diagram¶

Equipment¶

• Large gyroscope (Leybold 34818)

• Pointed rod

• Rod with cup

• Round disk with red, white and black segments

Presentation¶

The pointed support is shifted so that the gyroscope is supported at its centre of gravity. The gyroscope is made spinning at an angle of about $20^{\circ}$ with the vertical. The spinning gyroscope remains steady in space.

Now a short blow is given to the axis of the spinning gyroscope. It now performs an additional rotary motion; the axis moves conically. This movement is called nutation. If the colored segment is fixed on the top-side of the ball bearing, the instantaneous axis of spin is made visible. (Individual colors will be seen, but everywhere else they will merge to a uniform ‘grey’.)

Explanation¶

When the gyroscope is spinning, it has an angular momentum of $I_{0} \omega_{0}$ (see Figure 2a). When a short blow is given, an extra angular momentum ( $\triangle L$ ) is added to the spinning wheel (see Figure 2b; the short blow is given to the upper part of the axis in the direction of the observer). This leads to a total angular momentum $L$, which is constant from then on.

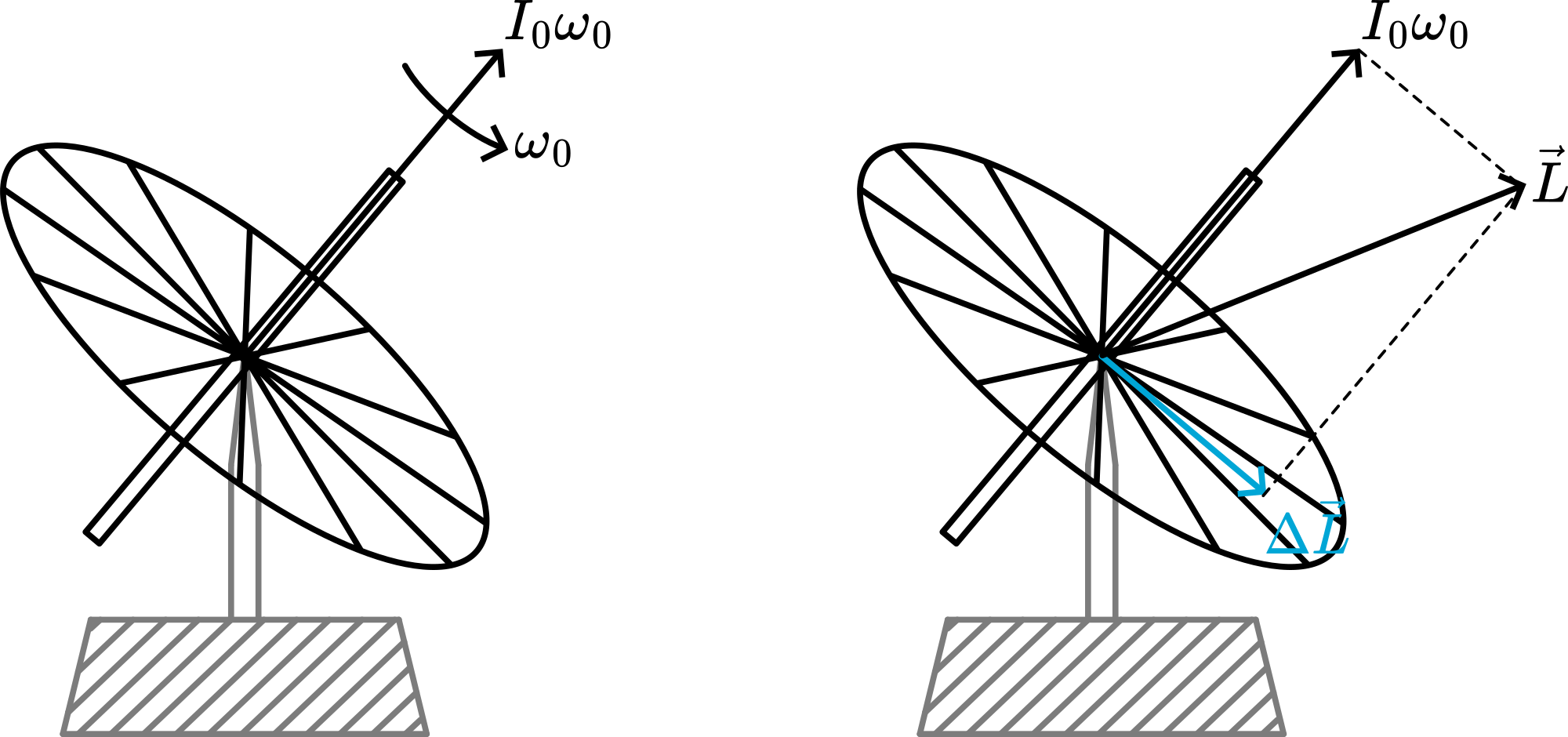
$\Delta L$ corresponds with a rotation $\omega^{'}=\frac{\Delta L}{I^{'}}$. The resultant of $\omega_{0}$ and $\omega^{'}$ is the momentary angular velocity $\omega$ (see Figure 3a). This resultant $\omega$ does not have the same direction as $L$, since $I^{'}<I_{0}$. The constant $\angle$ is, at any moment, the resultant of $I_{0} \omega_{0}$ and $I^{'} \omega^{'}$. This is reached only when the gyroscope moves in such a way that in the parallelogram of Figure 3b, the axis of momentary angular velocity moves in a cone around the fixed axis of $L$. Then also the symmetry-axis of the gyroscope moves in a cone around the axis of $L$. This cone is called the cone of nutation.

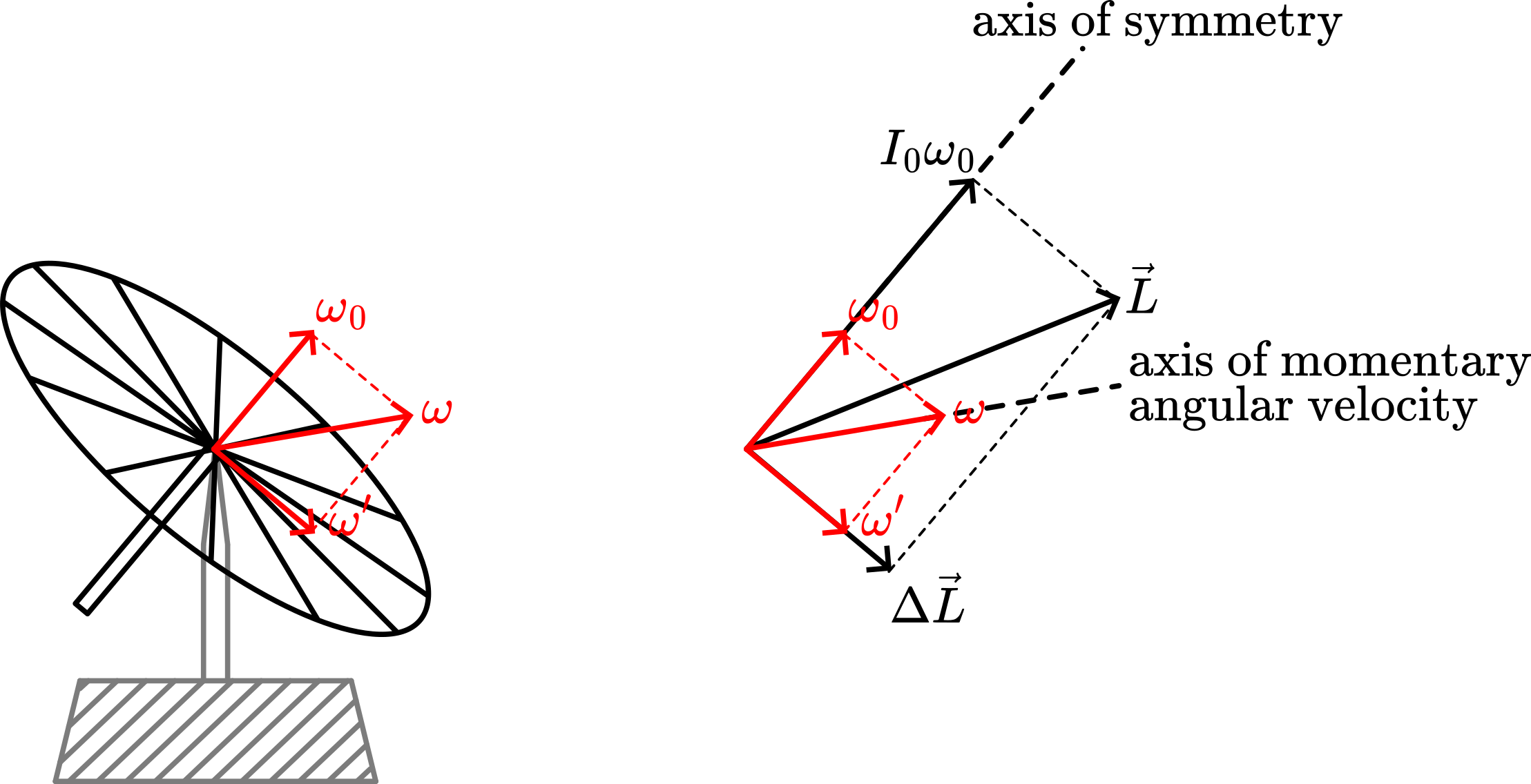
For the observer in the laboratory, this results in a rotation of the coplanar vectors $\omega_{b}$, $I_{0} \omega_{b}, \omega, \Delta L$ and $\omega^{'}$ around $L$. The cone described by the symmetry-axis around $L$ is called the cone of nutation; the cone described by $\omega$ around $L$ is called the space cone. For the observer in the rotating frame (e.g. seated on the symmetry-axis), the vector $\omega$ rotates around this axis, thus describing the so-called body cone. For the observer in the laboratory, this cone is not stationary, but moves around the space cone. Notice that the space cone and the body cone have the vector win common.

Remarks¶

• See also the description of the demonstration Nutation.

Sources¶

• Roest, R., Inleiding Mechanica, pag. 223

• Borghouts, A.N., Inleiding in de Mechanica, pag. 225

• Leybold Didactic GmbH, Gerätekarte, 34818