Millikan - Introduction to Experimentation in Physics

Millikan’s experiment is a classic physics experiment. The idea is that you can levitate small oil droplets between two capacitor plates. Because the charge is quantized and the mass and the applied electric field can be determined, you can determine the electric charge quantum.

Schematic setup of Millikan’s test, figure via Wikimedia Commons (commons)

Theory¶

For this experiment we use charged oil droplets that move with a constant velocity.

Constant velocity¶

When the droplets move at a constant speed, there is a frictional force at play. The magnitude of this force is given by Stokes’ law:

F_w=6\pi\eta rv

(1)

Here, $\eta$ is the viscosity of air, $r$ is the radius of the droplet and $v$ is the velocity of the droplet. This equation only holds under certain conditions. Since the droplets are small ( $0.5*10^{-6}$ )m, this is on the order of the free path of gas molecules ( $0.07*10^{-6}$ m) and a correction factor must be taken into account. This ensures that the no-slip condition does not apply at the edge of the droplets. The viscosity must therefore be divided by a correction factor of $k=1+\frac{b}{p\cdot r}$ where the correction factor is $b=80 \mu \textrm{m} \cdot \textrm{hPa}$ , $p$ is the pressure in Pa and $r$ is the radius of the droplet (in m).

For the droplet’s radius it holds:

r = \sqrt{\frac{18\eta v_g}{4g(\rho_d - \rho_l)}}

(2)

where $v_g$ is the velocity without an external electric field.

The forces acting on a charged oil droplet moving at a constant velocity.

A trick we can use is to reverse the electric field. By adding the force balance for a cooperating electric field and a counteracting electric field (against gravity), the gravitational term is eliminated.

Equipment¶

The equipment present includes:

a. A Millikan cell with illumination possibilities.

b. An adjustable DC voltage source.

c. A voltmeter.

d. A microscope with an eyepiece slide with calibration scale.

e. A calibration scale.

f. An oil sprayer.

g. A telephone holder or webcam

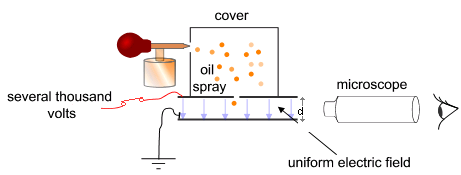
The experiment¶

In this experiment, the times are measured that a charged oil droplet needs to travel a certain distance in air, both with and without an electric field. The oil is atomized in the condenser by squeezing the oil atomizer. These droplets can then be followed with the eyepiece. The distance to be determined corresponds to the distance between two pre-selected lines on the calibration scale in the eyepiece.

To perform the experiment accurately, it is important to select droplets of different sizes and with charges ( $q$ ) smaller than about 10 times the elementary charge. This means that you should focus your measurements on droplets whose transit times fall within specific intervals. Since the exact value of the elementary charge ( $e$ ) is not yet known, these intervals cannot be calculated directly. In theory, a rough experimental estimate of $e$ would first be needed to determine these intervals. Since there is not enough time for this, $e = 2 \cdot 10^{-19}\mathrm{~C}$ is assumed in the preparation of the experiment.

In addition, the following data from the Millikan device are required:

Distance between the plates of the Millikan cell: $(6.36 \pm 0.02) \cdot 10^{-3}$ m.
Distance between the lines on the calibration scale: $(\approx 1/20) \cdot 10^{-3}$ m.
Density of the oil: see measurements
Viscosity of air at room temperature: $1.8 \cdot 10^{-5}$ kg/m·s.
Voltage difference between the plates: adjustable from 0 to 600 V.

Preparation¶

As part of the preparation, calculate in which intervals the transit times must be approximately so that the charge of the droplet is smaller than approximately 10 electron charges.

Determine the transit times for a number of droplets and calculate their charges $q$ from this. If necessary, apply the correction to Stokes’ law. The constant that plays a role in this has a value of approximately $8.2\cdot10^1$ Nm $^{-1}$ .

Calculate $e$ from the charges found. Do this graphically, for example. Remember that $q = ne$ with $n$ integer, so that $q$ plotted against $n$ must yield a straight line through the origin. To find this straight line, plot the found $q$ values vertically and $n$ horizontally. All points ( $n$ , $q$ ) in the plane are possible points of this straight line. Draw a straight line through the origin so that $q = ne$ is satisfied as well as possible. $e$ follows from the slope coefficient of this line.

Measuring oil density¶

### Siliconenolie

V_so = np.array([0, 1.9, 1.7, 1.55, 1.40, 1.10, 1.0, .75, .55, .4, .25]) #mL
m_so = np.array([3.48, 5.56, 5.36, 5.20, 5.00, 4.73, 4.54, 4.36, 4.12, 3.94, 3.80 ]) - 3.48 #g

# Petroleumolie

V_po = np.array([4.4, 4.5, 5.3, 6.8, 7.2, 9.3, 9.4, 11.6, 13.9, 14.6, 16.9, 18.9]) #mL
m_po = np.array([3.40, 3.56, 3.95, 5.30, 5.57, 7.15, 7.36, 9.06, 10.89, 11.57, 13.38, 14.9 ]) #g

First experiment

Falling waterdroplet