Thermolabs
Abstract¶
Here we describe our project related to the topic of thermodynamics as devised for a renewed curriculum.
Introduction¶
- New curriculum
- Projects in which simulations, project work and labs are central and serve as link between courses and thereby aim at conceptual development / strengthening
- Here describe thermodynamics
- expensive experiments, single setup - or engineer it
- ...
Physics background¶
We here utilize the method devised by Clément and Desormes {see e.g. [ref]} which makes use of an adiabatic process where a pressured gas (state1: ) in a cylinder with volume is suddenly released. In our case we use a fire extinguisher where the gas is released by opening the valve. As the pressure suddenly drops the temperature in the cylinder decreases as the gas is doing work. When the pressure inside the cylinder equals the atmospheric pressure (state 2: ) we close the valve. The temperature of the gas inside the cylinder increases and hence the pressure increases until equilibrium is reached (state 3: ), and hence the pressure increases to a value - no work is being done and here we make the assumption that the heat capacity of the cylinder is much larger than the heat capacity of the gas. The venting (state 1 state 2) is adiabatic; the reheating (state 2 state 3) is isochoric with heat from the vessel; overall, the vessel acts as a large reservoir returning the gas to .
The first part of the process can be described by the Poisson equations for an adiabatic process:
where is the specific heat ratio given by . We note that and . The second part of the process can be described using Gay-Lussac’s relation:
where we consider (again) that and . Rearranging these equations (see Appendix) yields:
Methods & Materials¶
We use an ‘old’ fire fire extinguisher as vessel and a an Arduino MKR Zero with onboard sd-card module as data logger, see {numref}‘fig_experimental_setup_1’. An Adafruit MPL3115A2 is used to measure both temperature and pressure. The sensor is able to detect small pressure changes (+/- 0.05kPa) but is limited in range. We repeat the measurements with the XXX sensor which allows to measure at higher pressures.
The sensor and a LiPo battery are mounted to the Arduino. The entire instrument was then mounted on a regular pvc-tube which is in return mounted on the valve.

Figure 1:placeholder for device
To ensure that minimal water vapor is present in the vessel, we blow nitrogen gas into the vessel before closing it. Interval... To obtain proper results, we waited half an hour before filling the vessel with nitrogen gas up to a pressure of . Again, for the best results, we waited half an hour before opening the valve. After the pressure inside the vessel reaches atmospheric pressure. We kept recording pressure and temperature for half an hour.
Using equation (3) we calculate the specific heat ratio.

Figure 2:Arduino as logger
Results¶
Source
# # Metingen aan brandblusser prototype
# - meting thermoblus is tweede test
# - meting TEMP005 is een zeer lange meting
# - N2 is meting waarbij we gevuld hebben met stikstof
import numpy as np
import matplotlib.pyplot as plt
#data = np.loadtxt('meting thermoblus.csv', delimiter=',', skiprows=1)
#data = np.loadtxt('TEMP005.csv', delimiter=',', skiprows=1)
#data = np.loadtxt('N2.csv', delimiter=',', skiprows=1) # vullen met stikstof
data = np.loadtxt('TEMP005.csv', delimiter=',', skiprows=1) # lange meting
t = data[:,0]*1e-3
temp = data[:,1]
pressure = data[:,2]
fig, ax1 = plt.subplots(figsize=(8, 5))
#plt.title('Temperature and Pressure vs Time')
color_temp = 'tab:blue'
ax1.set_xlabel('Time (s)')
ax1.set_ylabel('Temperature (°C)', color=color_temp)
ax1.plot(t, temp, color=color_temp, label='Temperature (°C)')
ax1.tick_params(axis='y', labelcolor=color_temp)
ax1.grid()
ax2 = ax1.twinx()
color_pressure = 'tab:orange'
ax2.set_ylabel('Pressure (Pa)', color=color_pressure)
ax2.plot(t, pressure, color=color_pressure, label='Pressure (hPa)')
ax2.tick_params(axis='y', labelcolor=color_pressure)
fig.tight_layout()
plt.savefig('../Figuren/temperature_pressure_plot.svg')
plt.savefig('../Figuren/temperature_pressure_plot.png',dpi=450)
plt.show()Output
Source
# # Metingen aan brandblusser prototype
# - meting thermoblus is tweede test
# - meting TEMP005 is een zeer lange meting
# - N2 is meting waarbij we gevuld hebben met stikstof
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets
#data = np.loadtxt('meting thermoblus.csv', delimiter=',', skiprows=1)
#data = np.loadtxt('TEMP005.csv', delimiter=',', skiprows=1)
#data = np.loadtxt('N2.csv', delimiter=',', skiprows=1)
data = np.loadtxt('TEMP005.csv', delimiter=',', skiprows=1) # lange meting
t = data[:,0]*1e-3
temp = data[:,1]
pressure = data[:,2]
def update(t_c):
plt.clf()
fig, ax1 = plt.subplots(figsize=(8, 5))
#plt.title('Temperature and Pressure vs Time')
color_temp = 'tab:blue'
ax1.set_xlabel('Time (s)')
ax1.set_ylabel('Temperature (°C)', color=color_temp)
ax1.plot(t, temp, color=color_temp, label='Temperature (°C)')
ax1.plot(t[t_c], temp[t_c], 'ro') # Highlight the selected time
ax1.tick_params(axis='y', labelcolor=color_temp)
ax1.set_ylim([min(temp)-2, max(temp)+2])
ax1.grid()
ax2 = ax1.twinx()
color_pressure = 'tab:orange'
ax2.set_ylabel('Pressure (Pa)', color=color_pressure)
ax2.plot(t, pressure, color=color_pressure, label='Pressure (hPa)')
ax2.plot(t[t_c], pressure[t_c], 'ro') # Highlight the selected time
ax2.tick_params(axis='y', labelcolor=color_pressure)
ax2.text(0.5, 0.9, f'Time: {t[t_c]:.2f} s\nTemp: {temp[t_c]:.2f} °C\nPressure: {pressure[t_c]:.2f} hPa',
transform=ax2.transAxes, fontsize=10, verticalalignment='top')
fig.tight_layout()
plt.show()
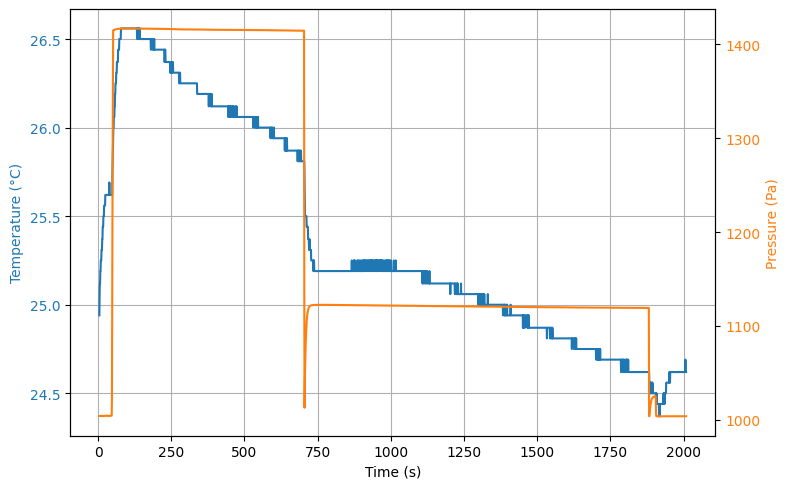
interact(update, t_c=widgets.IntSlider(min=0, max=len(t)-1, step=1, value=len(t)//2))Figure 3 shows the entire thermodynamic process, including the filling of the cylinder at . We note here that due to compression of the gas the temperature increases. Given the educational context, this is a surplus for students to see.
At the valve is opened and the pressure drops in from to . The expected temperature decrease is observed as well (). Once the valve is closed again, we see the pressure in the vessel increases quickly to a maximum of .
Figure 3:pressure and temperature as function of time
Source
P_1 = max(pressure)
P_b = min(pressure)
P_2 = np.mean(pressure[np.where((t > 1500) & (t < 1750))])
def calculate_gamma(P_1, P_b, P_2):
gamma = (np.log(P_1) - np.log(P_b))/(np.log(P_1) - np.log(P_2))
return gamma
gamma = calculate_gamma(P_1, P_b, P_2)
print(gamma)
g_1 = (calculate_gamma(P_1+5, P_b, P_2) - calculate_gamma(P_1-5, P_b, P_2))/2
g_2 = (calculate_gamma(P_1, P_b+5, P_2) - calculate_gamma(P_1, P_b-5, P_2))/2
g_3 = (calculate_gamma(P_1, P_b, P_2+5) - calculate_gamma(P_1, P_b, P_2-5))/2
error_gamma = np.sqrt(g_1**2 + g_2**2 + g_3**2)
print(error_gamma)
Output
1.4645773337215904
0.035605767159031285
Using equation (3) we find a value for the specific heat ratio of where the literature value is known to be ... .
Source
# Vullen
low_t = 40
high_t = 200
fig, ax1 = plt.subplots(figsize=(8, 5))
color_temp = 'tab:blue'
ax1.set_xlabel('Time (s)')
ax1.set_ylabel('Temperature (°C)', color=color_temp)
ax1.plot(t[low_t:high_t], temp[low_t:high_t], color=color_temp, label='Temperature (°C)')
ax1.tick_params(axis='y', labelcolor=color_temp)
ax1.grid()
ax2 = ax1.twinx()
color_pressure = 'tab:orange'
ax2.set_ylabel('Pressure (Pa)', color=color_pressure)
ax2.plot(t[low_t:high_t], pressure[low_t:high_t], color=color_pressure, label='Pressure (Pa)')
ax2.tick_params(axis='y', labelcolor=color_pressure)
fig.tight_layout()
plt.title('Temperature and Pressure vs Time')
plt.show()Output
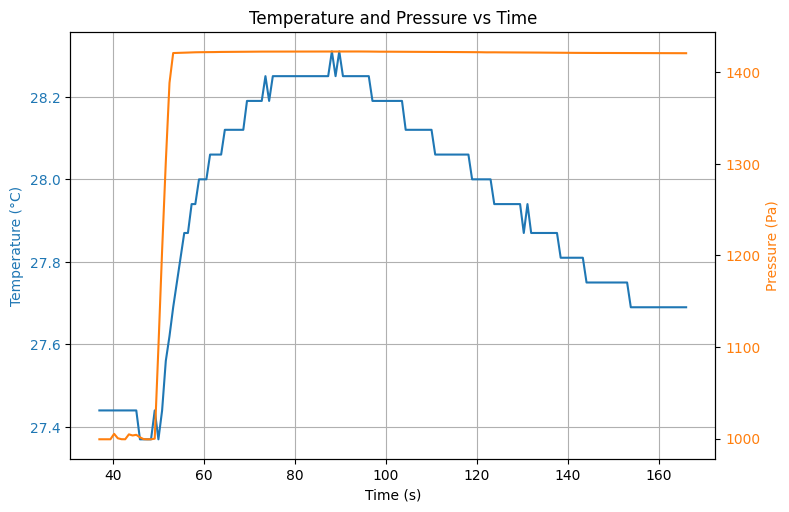
Source
# Leeg lopen
low_t = 440
high_t = 800
fig, ax1 = plt.subplots(figsize=(8, 5))
color_temp = 'tab:blue'
ax1.set_xlabel('Time (s)')
ax1.set_ylabel('Temperature (°C)', color=color_temp)
ax1.plot(t[low_t:high_t], temp[low_t:high_t], color=color_temp, label='Temperature (°C)')
ax1.tick_params(axis='y', labelcolor=color_temp)
ax1.grid()
ax2 = ax1.twinx()
color_pressure = 'tab:orange'
ax2.set_ylabel('Pressure (Pa)', color=color_pressure)
ax2.plot(t[low_t:high_t], pressure[low_t:high_t], color=color_pressure, label='Pressure (Pa)')
ax2.tick_params(axis='y', labelcolor=color_pressure)
fig.tight_layout()
plt.title('Temperature and Pressure vs Time')
plt.show()Output
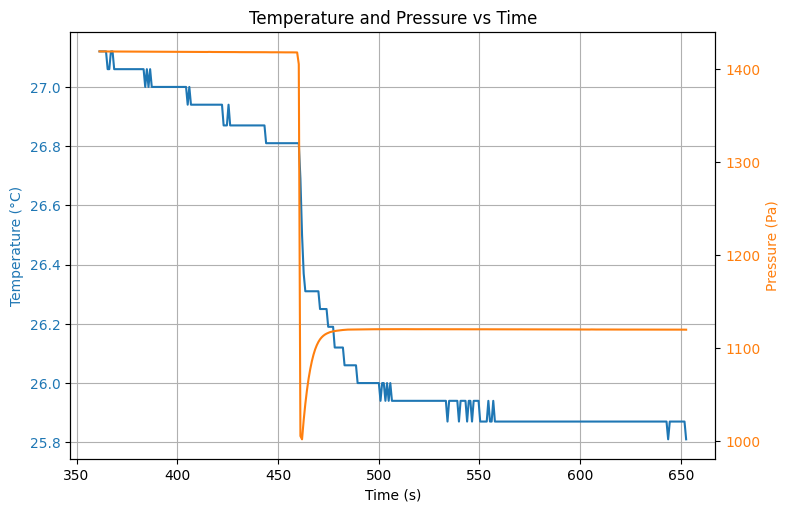
Source
# Naar eindtemperatuur
low_t = 600
high_t = 4000
fig, ax1 = plt.subplots(figsize=(8, 5))
color_temp = 'tab:blue'
ax1.set_xlabel('Time (s)')
ax1.set_ylabel('Temperature (°C)', color=color_temp)
ax1.plot(t[low_t:high_t], temp[low_t:high_t], color=color_temp, label='Temperature (°C)')
ax1.tick_params(axis='y', labelcolor=color_temp)
ax1.grid()
ax2 = ax1.twinx()
color_pressure = 'tab:orange'
ax2.set_ylabel('Pressure (Pa)', color=color_pressure)
ax2.plot(t[low_t:high_t], pressure[low_t:high_t], color=color_pressure, label='Pressure (Pa)')
ax2.tick_params(axis='y', labelcolor=color_pressure)
fig.tight_layout()
plt.title('Temperature and Pressure vs Time')
plt.show()Output
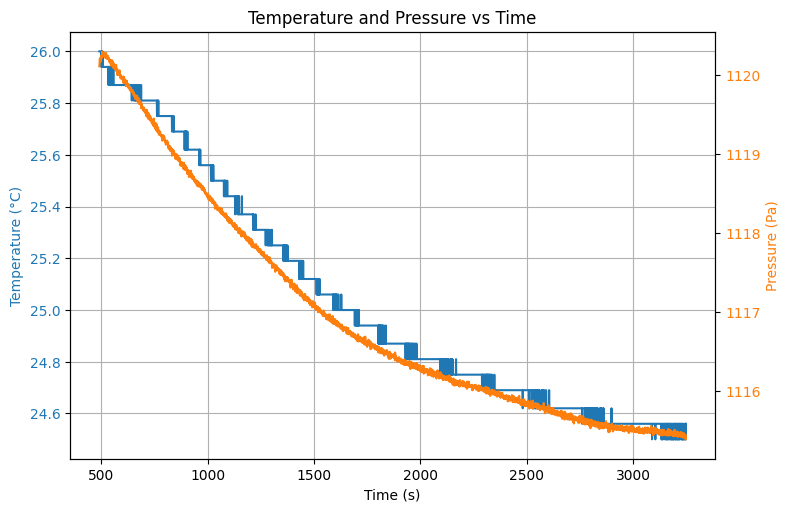
# Naar eindtemperatuur
low_t = 600
high_t = 4000
fig, ax1 = plt.subplots(figsize=(8, 5))
color_temp = 'tab:blue'
ax1.set_xlabel('Temperature')
ax1.set_ylabel('Pressure', color=color_temp)
ax1.plot(temp[low_t:high_t], pressure[low_t:high_t], color=color_temp, label='Temperature (°C)')
ax1.tick_params(axis='y', labelcolor=color_temp)
ax1.grid()
fig.tight_layout()
plt.title(' Pressure vs Temperature ')
plt.show()
Discussion & Conclusion¶
Our aim was to devise a cheap (scalable) but accurate experiment in the topic of thermodynamics. Determining the specific heat ratio using the valve of a fire entinguisher and an arduino as logger ... more process than expected (filling)
Appendix¶
Setup and assumptions¶
- Ideal gas in a rigid vessel of volume .
- State (1): initial equilibrium at .
- Rapid vent to atmosphere (no heat exchange during the short release) to State (2): pressure equals barometric pressure , temperature drops to .
- Valve is then closed; gas reheats at constant volume (no work) back to , reaching State (3): pressure .
- The quick release (1)(2) is adiabatic; the recovery (2)(3) is isochoric.
Step 1 — Adiabatic release (1)(2)¶
For a reversible adiabatic process of an ideal gas,
Thus,
Step 2 — Isochoric reheat (2)(3)¶
At constant , . Hence,
Step 3 — Eliminate and solve for ¶
Insert (A2) into (A1) and cancel :
Take natural logs and rearrange:
This matches the expression quoted in the main text, with .