03 Dropping Lead Shot

Aim¶

• To demonstrate the mechanical equivalent of heat.

Subjects¶

• 4B60 (Mechanical Equivalent of Heat)

Diagram¶

Equipment¶

• A 1 meter long perspex tube filled with 0.100 kg lead shot, and a thermistor mounted inside the tube.

• Data acquisition to display the temperature reading (PASCO).

Presentation¶

The tube is rotated several times over 180 degrees, such that the lead shot drops from one end of the tube to the other end (see the enlarged Figure 2).

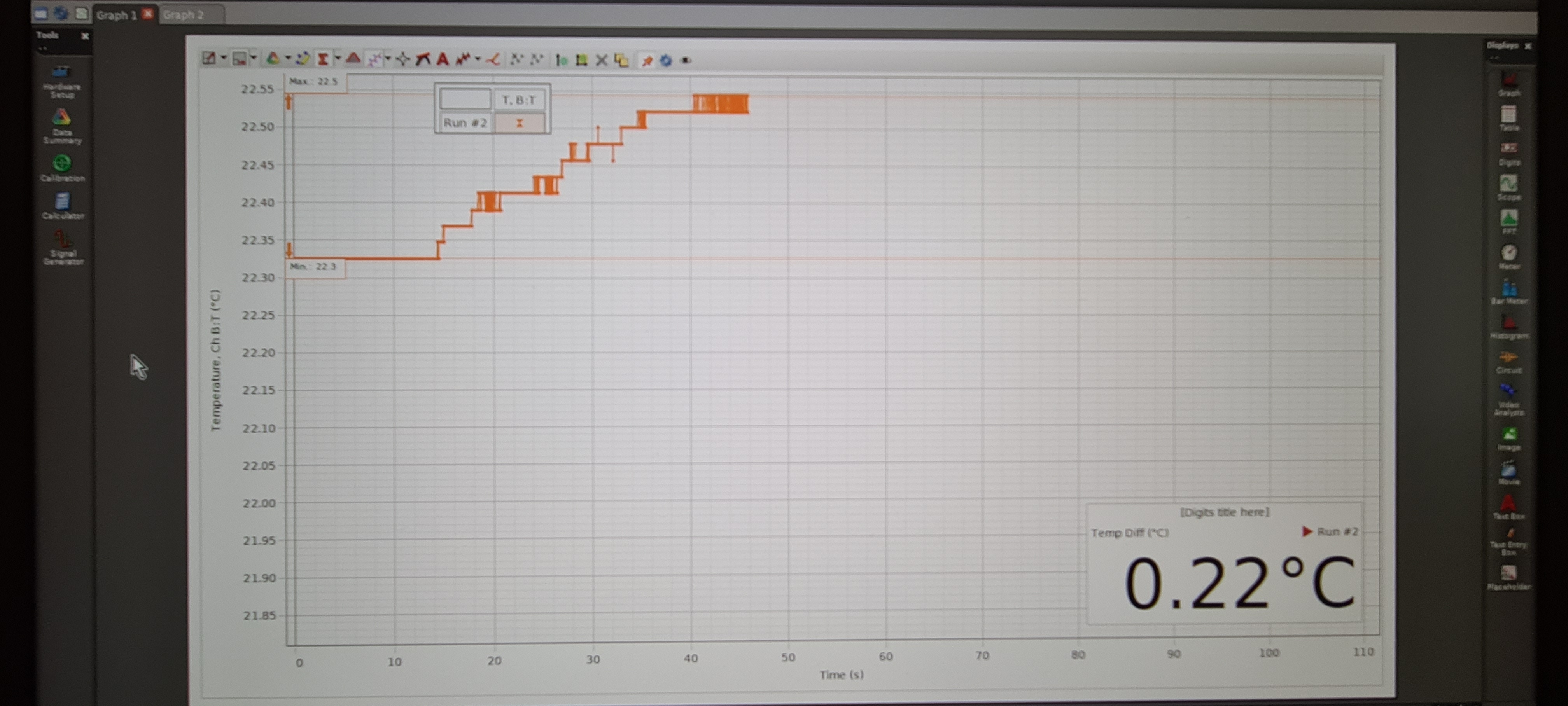
The temperature and the temperature rise is displayed real time (see the inset in the graph in Figure 3).

Explanation¶

This demonstration illustrates the conversion of mechanical energy into heat energy. The temperature rise of the lead shot is readily calculated as follows:

Given that the 1 meter tube is rotated 13 times means that the lead shot effectively drops over a height $h$ of 13 meters. Assume that the conversion between potential energy $E_{p} = mgh$, kinetic energy $E_{k}$, and internal energy $U = m_{Pb}C_{p,Pb}\Delta{T}$ is perfect, the potential energy can be equated to the internal energy of the lead shot, i.e:

$m_{Pb}gh = m_{Pb}C_{p,Pb} \Delta T$

Solving for the temperature rise $\Delta{T}$, and given that lead has a specific heat capacity of $C_{p,Pb} = 130 \mathrm{J} \cdot kg^{-1} \cdot K^{-1}$, the dropping height $h = 13 m$, and the gravitational acceleration is $g = 9.81 \mathrm{m/s^{2}}$, we obtain:

$\Delta{T} = \frac{gh}{C_{p,Pb}} = \frac{9.81 \cdot 13}{130} \approx 1^{\circ}\mathrm{C}$

The measured temperature rise is significantly lower and is approxmately $\Delta{T} \approx 0.26^{\circ}{C}$, which is probably due to the following factors:

• not only does the lead shot heat up, but also other materials, such as the alluminium plate onto which the thermistor is fixed (note that the mass of the lead shot drops out of the first expression)

• poor thermal conductivity between the lead shot and the thermistor

• the lead shot slides down the tube instead of falling from one end to the other end of the tube

Taking into account the heat capacity of the alluminium plate, the conservation of mechanical energy gives:

$m_{Pb}gh = m_{Pb}C_{p,Pb} \Delta{T_{Pb}} + m_{Al}C_{p,Al} \Delta{T_{Al}}$

and if we assume that the temperature rise of the alluminium plate with a mass of $m = 0.006 \mathrm{kg}$ and a specific heat capacity of $C_{p,Al} = 900 \mathrm{J} \cdot kg^{-1} \cdot K^{-1}$ and of the lead shot is the same (i.e. $\Delta{T_{Pb}} = \Delta{T_{Al}}$), we obtain for the temperature rise:

$\Delta{T} = \frac{m_{Pb}gh}{m_{Pb}C_{p,Pb} + m_{Al}C_{p,Al}}$

or:

$\Delta{T} = \frac{0.100 \cdot 9.81 \cdot 13}{0.100 \cdot 130 + 0.006 \cdot 900}\approx 0.69^{\circ}\mathrm{C}$

This is a more accurate estimate of the actual temperature rise.

Remarks¶

• Ascertain that when the demonstration is performed, that after the final rotation the lead shot is at the end of the tube where the thermistor is mounted, such that the lead shot continues to give off its heat to the thermistor.

Sources¶