01 Clement’s and Desormes’ Experiment

Aim¶

• To show an adiabatic proces.

• To determine the ratio of the specific heats of a gas.

Subjects¶

• 4B70 (Adiabatic Processes)

Diagram¶

Equipment¶

• Large container (we use a 5 liter decantationbottle)

• valve with large opening, $10 \mathrm{~mm}$

• syringe, $100 \mathrm{ml}$

• U-tube manometer

Presentation¶

The valve of the container is closed. By means of the syringe an amount of air is pushed into the container. The manometer shows the raised pressure in the container $\left(h_{1}\right)$. Now the valve of the container is opened for a short time (just long enough to have the pressure in- and outside the container to be equal; about is in our situation). After closing the valve, the manometer shows that the pressure inside the container rises and after some time reaches a fixed value $\left(h_{2}\right)$.

The ratio of heat capacities, $C_{\rho} / C_{V}$ can now be determined by $\gamma=\frac{C p}{C V}=\frac{h_{1}}{h_{1}-h_{2}}$

Explanation¶

The air in the container and syringe is at room temperature $T_{0}$ and pressure $p_{0}$. Pressing the syringe raises the pressure to $p_{1}$. The manometer reads $h_{1}$. (See Figure 2.)

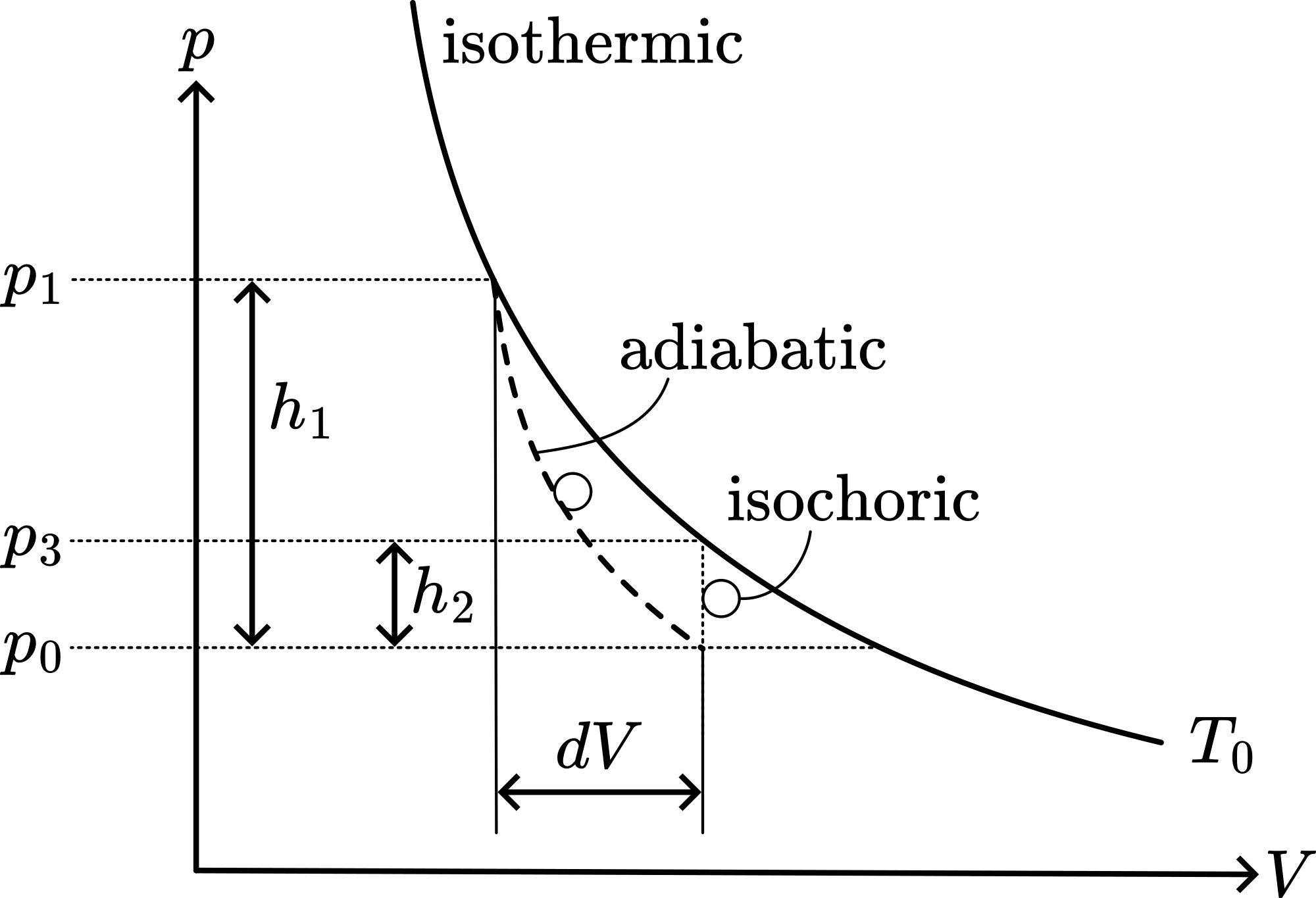
Opening the valve makes the air expand adiabatically to pressure $p_{0}$ and temperature falls to $T_{2}$. The valve is quickly closed and now the trapped air in the container raises isochorically in temperature to $T_{0}$ and pressure $p_{3}$. The manometer reads $h_{2}$. Consider the isothermic - and adiabatic process:

Isothermic: $p V=$ const. $V d p+p d V=O\left(\frac{d y}{d V}\right)_{i}=-\frac{p}{V}$

Adiabatic: $p V^{r}=$ const., $V^{r} d p+p V^{r-1} d V=0,\left(\frac{d p}{d V}\right)_{a}=-\gamma \frac{p}{V}$

These two combined: $\left(\frac{d p}{d V}\right)_{a}=\gamma\left(\frac{d p}{d V}\right)_{i}$

Consider this for the same $d V$ in both processes (see Figure 2) and we find:

$\frac{d p_{a}}{d p_{i}}=\gamma=\frac{h_{1}}{h_{1}-h_{2}}$

Remarks¶

• It is easy to repeat the experiment a number of times.

• Instead of starting the experiment by pressing air into the container it can also be performed by sucking air out of it. (Figure 2 will be different, of course.)

Sources¶

• Freier, George D. and Anderson, Frances J., A demonstration handbook for physics, pag. H.14

• Grimsehl, Lehrbuch der Physik, part 1, pag. 473-475

• Aulis, Handbuch der Physik, part 4, pag. 65