Skip to article frontmatterSkip to article content

02 Newton’s Rings (2)

Aim

To show Newton’s rings, and that its color sequence is not a rainbow.

Subjects

Diagram

.

Figure 1:.

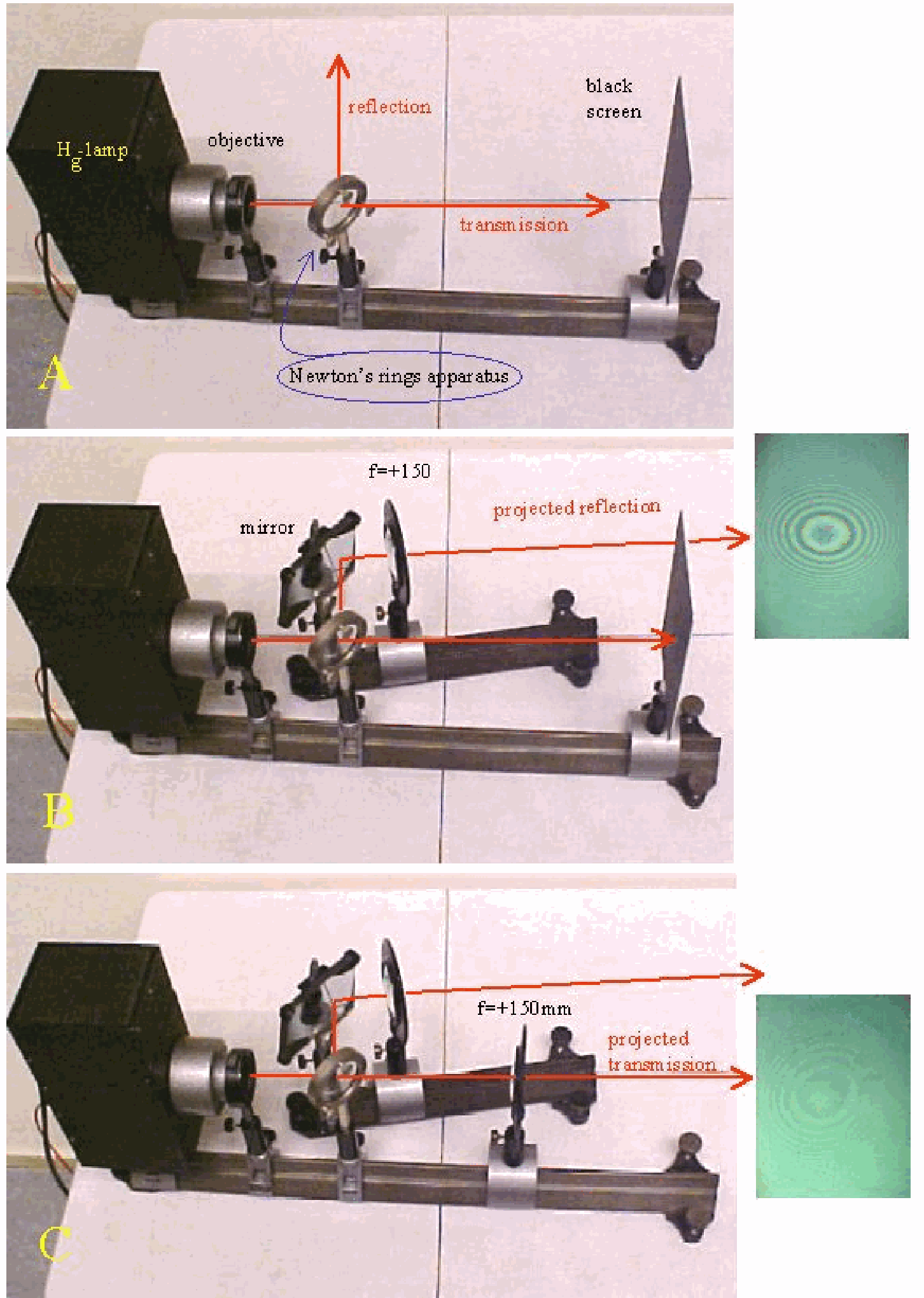
Equipment

Safety

Presentation

Set up the equipment as shown in Diagram. Images are projected on the wall (see Figure 2A)

.

Figure 2:.

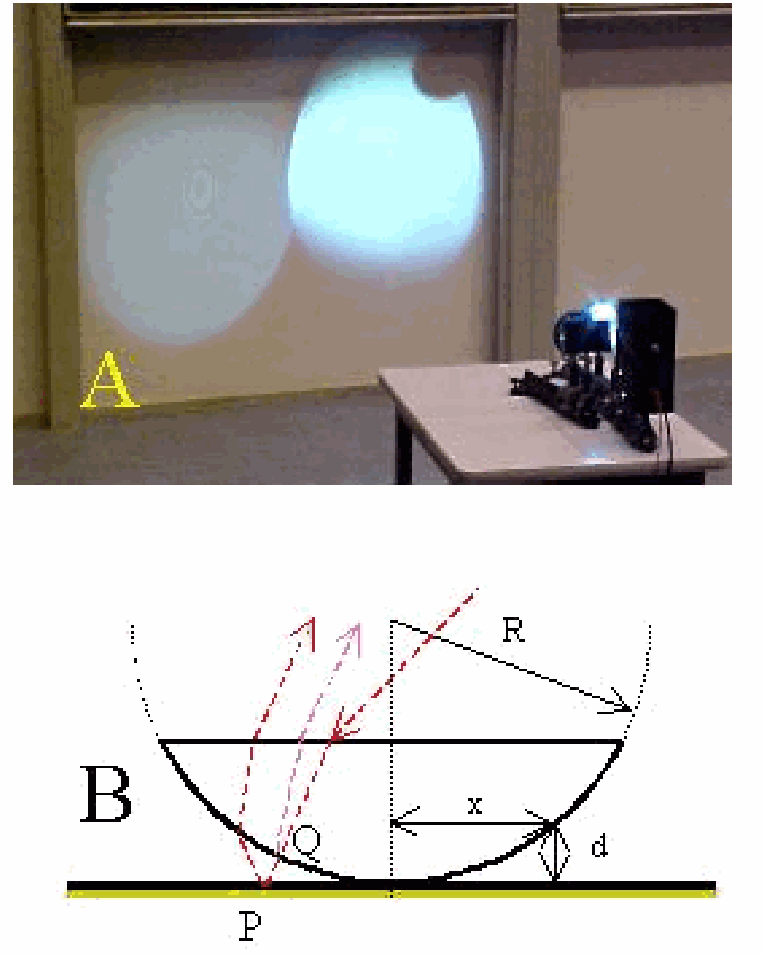
After the lamp is heated up, situation of Diagram A is presented to the students, to indicate that there will be a reflected and a transmitted beam of light. Then the transmitted beam is blocked (black screen) and using the mirror and a +150 mm+150 \mathrm{~mm}-lens the reflection image is projected (Diagram B). Clearly Newton’s rings are observed. Observe the central dark spot (see also: Remarks) observe the colored rings, the color-sequence and observe the diminishing distance between the rings when moving away from the centre. Changing the pressure on the Newton’s rings apparatus will change/move the reflected image. Then the black screen is removed and using the second +150 mm+150 \mathrm{~mm}-lens the transmitted image is projected next to the reflected image (see Diagram C and Figure 2). It is clearly visible that both images are complementary.

At first glance, the observed colors look rainbowlike, but careful observation shows that it differs from a rainbow (see Figure 3; reality is much better than this photograph).

.

Figure 3:.

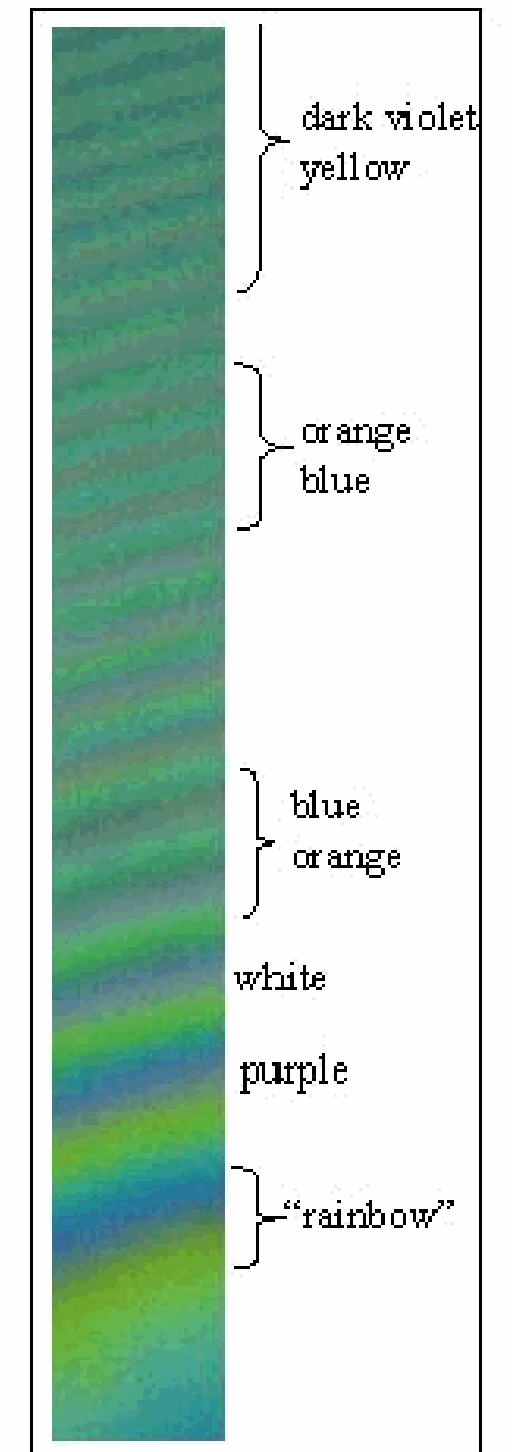
Observing the reflected image shows, when moving away from the central dark spot, at first a rainbow, but already in the next ring the color purple appears; in the next rings white and orange are dominating; around ring 10 there is a repeating sequence of blue and orange and around ring 16 repeating bands of dark violet and yellowish rings are visible giving form a distance the impression of a continuity of black and white fringes.

Explanation

See Figure 2 B. Looking at the two red rays drawn in this figure, we see that it is the height dd that introduces the phasedifference. d=R−(R2−x2)1/2d=R-\left(R^{2}-x^{2}\right)^{1 / 2}.

The two rays, one reflecting from the hemisphere and the other reflecting from the plane, will have a phasedifference of Δϕ=k(2d)−π\Delta \phi=k(2 d)-\pi ( π\pi at reflection off the plane).

Maximum, constructive interference will occur at Δφ=4πdλ−π=m2π\Delta \varphi=\frac{4 \pi d}{\lambda}-\pi=m 2 \pi, so when d=1/2λ(m+1/2)d=1 / 2 \lambda(m+1 / 2).

This result translated to the distance xx (because xx lies in the plane we are watching/projecting) yields 1/2λ(m+1/2)=R−(R2−x2)1/21 / 2 \lambda(m+1 / 2)=R-\left(R^{2}-x^{2}\right)^{1 / 2}, giving x={λR(m+1/2)x=\{\lambda R(m+1 / 2) 1/4λ2(m+1/2)2}1/2\left.1 / 4 \lambda^{2}(m+1 / 2)^{2}\right\}^{1 / 2}. And RR being much larger than λ\lambda will give x={λR(m+1/2)}1/2x=\{\lambda R(m+1 / 2)\}^{1 / 2}. First conclusion is that xx is proportional to the squareroot of wavelength. So a higher wavelength yields a higher xx. blue is on the inside, red on the outside. Second, the proportionality in (m+1/2)1/2(m+1 / 2)^{1 / 2} shows that the sequence of the bright fringes follows a square root: moving away from the centre the fringes come closer and closer together.

.

Figure 4:.

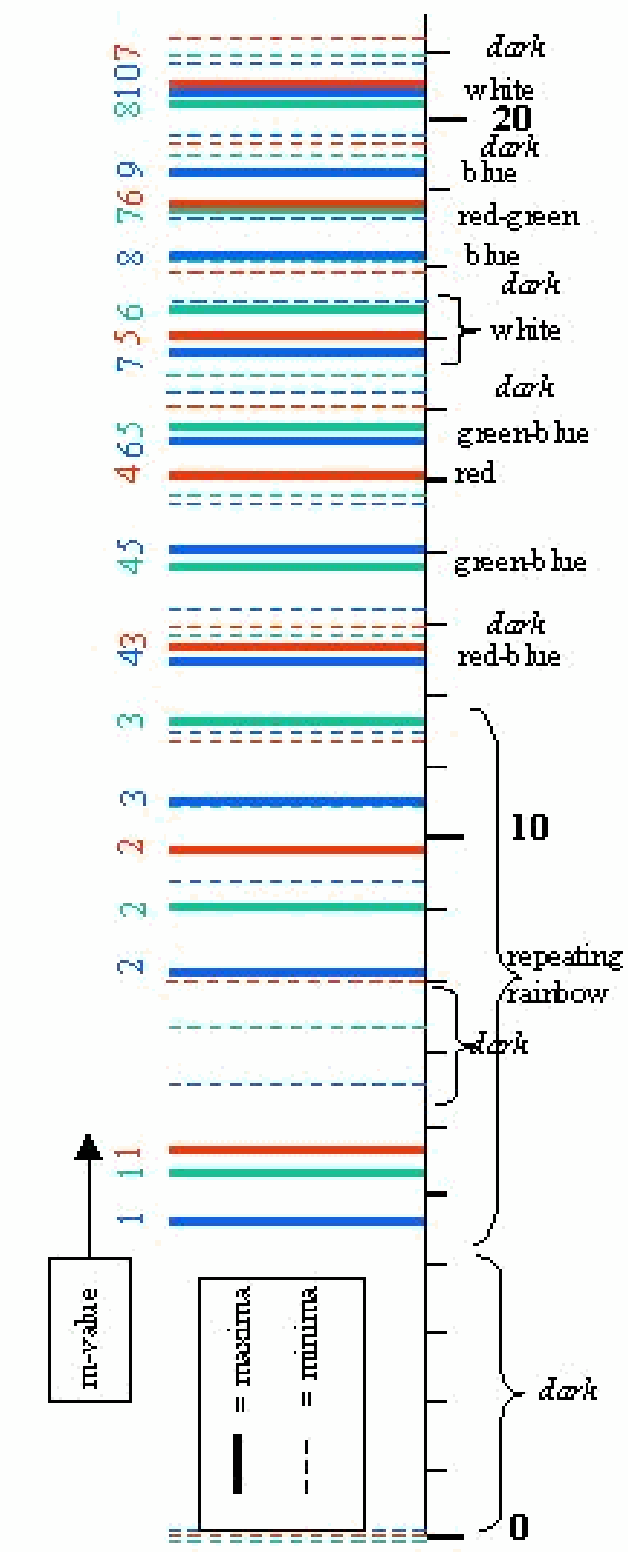
Finally, we calculated for a number of mm-values xx. Figure 4 shows the calculated results ( 10−5;R=1 m10^{-5} ; \mathrm{R}=1 \mathrm{~m} ) for the red, green and blue line of H0\mathrm{H}_{0}-light. In this way it is clear that the colours observed are the result of different combinations. Only near the centre a rainbow pattern appears.

It is not difficult now to show that for destructive interference we get x=(λR m)1/2x=(\lambda R \mathrm{~m})^{1 / 2}. This yields that the centre of the reflected Newton’s rings must be a dark spot. Figure 4 shows the minima as dashed lines for red, green and blue.

Remarks

Sources

6D30 Thin Films
01 Newton’s Rings (1)
6D30 Thin Films
03 Oil Film