Skip to article frontmatterSkip to article content

02 Centre of Rotation

Aim

To show that a free rotating body rotates around its centre of mass.

Subjects

Diagram

.

Figure 1:.

.

Figure 2:.

.

Figure 3:.

Equipment

Presentation

The two spheres, connected by a light stick, are balanced (see Figure 1) to show where the centre of mass (CM\mathrm{CM}) is located. The location of the CM\mathrm{CM} divides the distance ( dd ) between the two centres of the spheres in roughly 13d\frac{1}{3} d and 23d\frac{2}{3} d.

The system of two spheres connected by a twisted rubber band (see Figure 1 and Remarks) is placed on the gridboard, and then left by itself. The system begins to rotate as the twisted rubber band unwinds. The system rotates around a fixed point. This can be recognized as the CM\mathrm{CM}. This can be related to the first part of the demonstration. Note that during the rotation, the distance between the spheres increases, but its centre of rotation keeps the ratio 13:23\frac{1}{3}:\frac{2}{3}!

Explanation

As no external forces are acting, the CM\mathrm{CM} has to remain at its position on the board according to Newton’s first law. (Note: When the system rotates around any other point but the CM\mathrm{CM}, the CM\mathrm{CM} performs a rotation, and an external torque should be needed for that.)

.

Figure 4:.

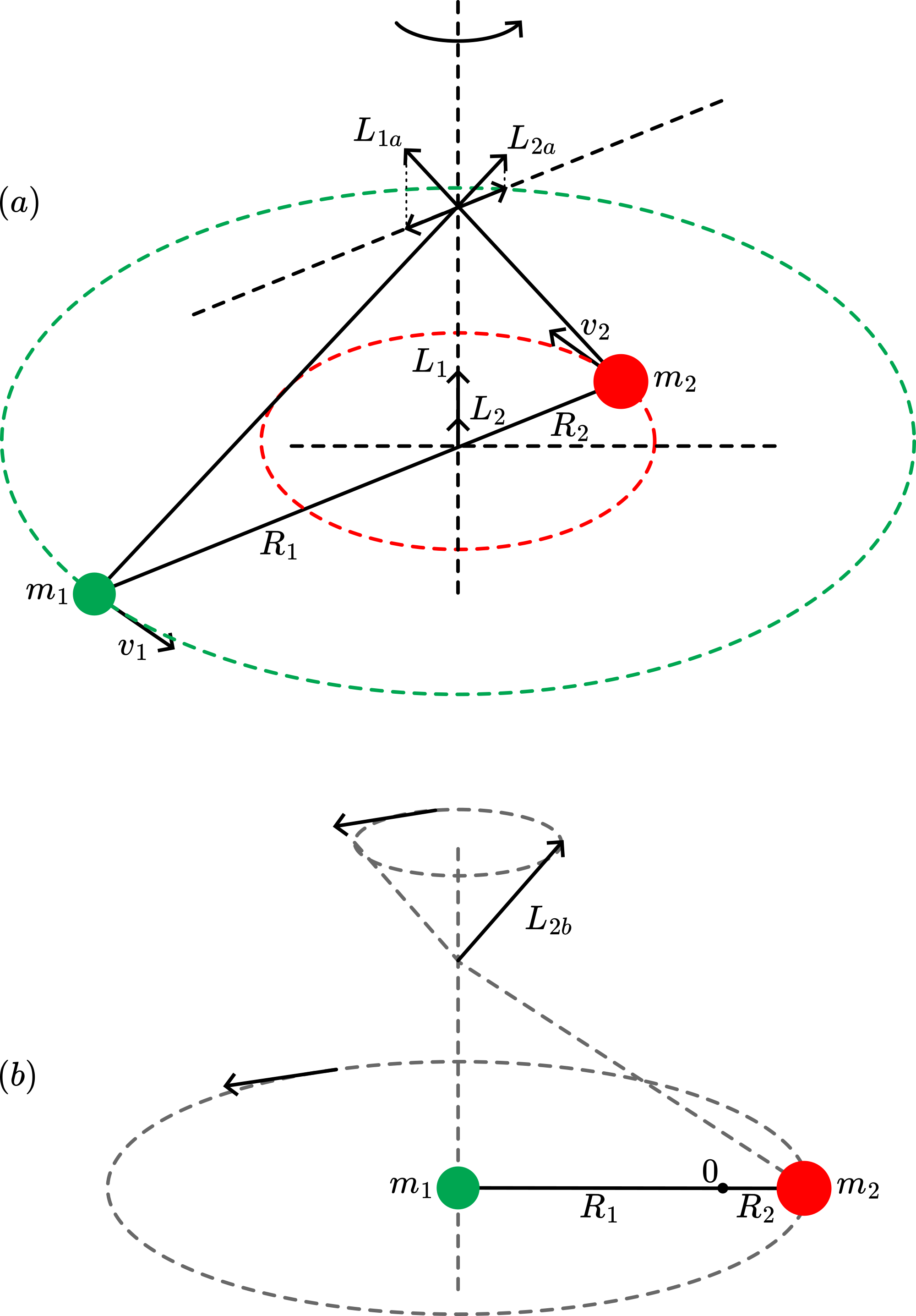
The body rotates around an axis perpendicular to dd. When no external forces are acting, the angular momentum vector L⃗\vec{L} remains constant. The body in our demonstration consists of two masses: m1m_{1} and m2m_{2} (see Figure 4a).

L⃗=L⃗1+L⃗2L⃗=R⃗1×m1v⃗1+R⃗2×m2v⃗2\begin{aligned} \vec{L}&=\vec{L}_{1}+\vec{L}_{2}\\ \vec{L}&=\vec{R}_{1} \times m_{1} \vec{v}_{1}+\vec{R}_{2} \times m_{2} \vec{v}_{2} \end{aligned}
(1)

The axis of rotation characterizes itself by the fact that, at any position on this axis, L⃗\vec{L} will have the same magnitude and direction (at O′O^{'} the horizontal components of L1aL_{1 a} and L2aL_{2 a} cancel, and their vertical components add up to L⃗\vec{L}: see Sources). This means that only one axis of rotation is possible. When, for instance, an axis of rotation is chosen passing through the centre of m1\mathrm{m}_{1}, then the total angular momentum adds up to L2bL_{2 b} (see Figure 4 b). And so, being constant in magnitude, its direction constantly changes (describing a cone). Such a situation needs an external torque.

In our demonstration, there is no external torque, and the sphere-system rotates around an axis somewhere between the two spheres (Figure 5). At OO, L⃗=R⃗1×m1v⃗1+R⃗2×m2v⃗2\vec{L}=\vec{R}_{1} \times m_{1} \vec{v}_{1}+\vec{R}_{2} \times m_{2} \vec{v}_{2}, directed along the axis of rotation. At O′O^{'}, the horizontal components of L1L_{1} and L2L_{2} need to cancel in order to keep LL along the axis of rotation.

∣L⃗1∣=R1m1v1cos⁡α\left|\vec{L}_{1}\right|=\frac{R_{1} m_{1} v_{1}}{\cos \alpha}
(2)
L1h=R1m1v1cos⁡αsin⁡α=R1m1v1tan⁡α=m1v1yL_{1 h}=\frac{R_{1} m_{1} v_{1}}{\cos \alpha} \sin \alpha=R_{1} m_{1} v_{1} \tan \alpha=m_{1} v_{1} y
(3)

In the same way:

L2h=m2v2y,v=ωR, so L1h=m1ωR1yL1h=m1ωR1yL_{2 h}=m_{2} v_{2} y, v=\omega R \text{, so } L_{1 h}=m_{1} \omega R_{1} y L_{1 h}=m_{1} \omega R_{1} y
(4)

and

L2h=m2ωR2yL2h=m2ωR2yL_{2 h}=m_{2} \omega R_{2} y L_{2 h}=m_{2} \omega R_{2} y
(5)

These two are equal when m1R1=m2R2m_{1} R_{1}=m_{2} R_{2}, this holds when the axis of rotation passes through the CM\mathrm{CM}.

.

Figure 5:.

Remarks

Sources

1D40 Center of Mass
01 Centre of Mass
1D40 Center of Mass
03 Student’s Centre of Mass