02 Boomerang Ball (1)

Aim¶

To explain the very peculiar behavior of a bouncing superball.

Subjects¶

• 1K10 (Dynamic Torque)

• 1N10 (Impulse and Thrust)

Diagram¶

Equipment¶

• Superball.

• Basketball.

• Table.

Safety¶

• A superball can jump into many unexpected directions, so mind vulnerable objects in your neighborhood.

Presentation¶

The superball is thrown under the table as shown in the Diagram. Surprisingly it bounces back to the pitcher! How is this possible?

Explanation¶

As an introduction to an explanation a basketball is rolled over the floor, hitting the wall and rolling back to you. But in this rolling back it is also bouncing up and down. Confronting your students with the question “where originates this vertical momentum?” will lead them (I hope) to the answer: “the impulse of the friction force while the ball touches the vertical wall”.

As a second introduction to an explanation the basketball is thrown as shown in Figure 2A.

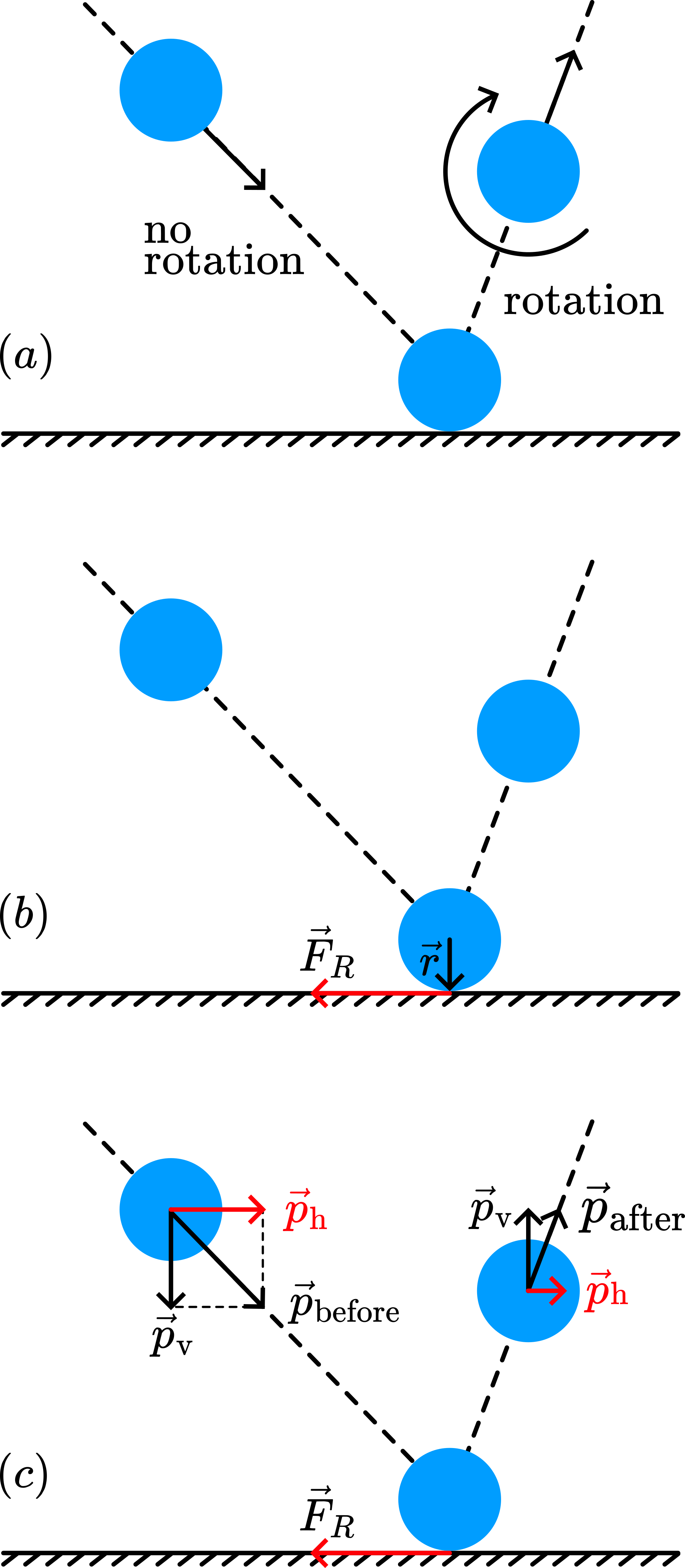
(Also see the demonstration [“Throwing a basketball”](../1K1005 Throwing a Basketball/1K1005.md)). The ball is thrown without rotation, but after bouncing it rotates (the lines on the basketball make this rotation very well visible). The cause for this rotation is the torque $\vec{M}$, due to the friction force $\vec{F}_{r}:\left(\vec{M}=\vec{r} \times \vec{F}_{r}\right)$ (see Figure 2B). $\vec{F}_{r}$, that acts during a certain time $\Delta t$, also causes a decrease of the momentum ( $\left.\Delta p_{h}\right)$ in the horizontal direction of the moving ball ( $\Delta \stackrel{\rightharpoonup}{p}_{h}=\int_{0}^{\Delta t} \vec{F}_{R} d t$ ). The result is that, after hitting the floor, the ball not only rotates but also rises at a steeper angle than it had in its approach. (See Figure 2C; $p_{v}$ only reverses its direction and does not change its magnitude; suppose the bounce completely elastic). Figure 3 shows the ball on hitting the bottom-side of the table-top. Observing the movement of the ball’s surface with respect to the bottom-side of the tabletop makes clear that the friction force is (again) directed to the left.

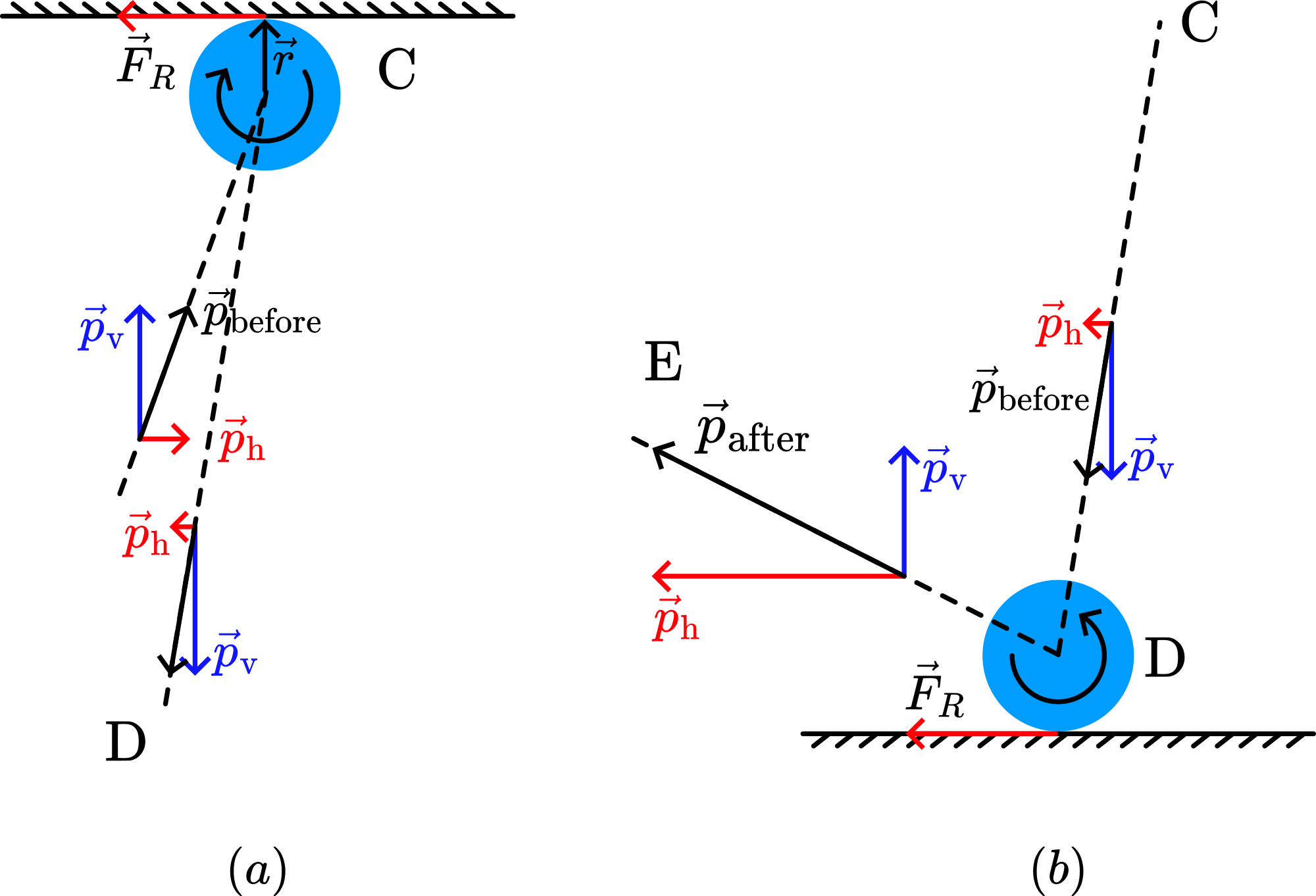
Due to this horizontal impulse, $p_{h}$ even changes direction and bouncing from the bottom side, the ball even moves to the left. (The clockwise rotation will be slowed down, stopped or even reversed, because on hitting the bottom-side of the tabletop $\bar{M}$ is directed in the opposite direction.)

Depending on the value of $p_{h}$ now, CD in Figure 3 could be a possible line of movement. Explaining line DE (towards the pitcher) will be easy when you suppose a counterclockwise rotation in the path CD, because then the friction force on hitting the floor is directed again to the left increasing the horizontal component of the ball’s velocity to the left! (see Figure 3B)

Remarks¶

• In theory all balls will behave in this way. Yet a superball is needed to show this type of “boomerang-behavior”. That a superball performs so well is due in the first place to its high coefficient of friction and subsequently its high friction force on horizontal contact with the floor and table. And a high friction force can change the horizontal momentum dramatically.

• It is more spectacular to throw the ball between the floor and the ceiling of the lecture room! (Even in our lecture hall that is around 7 meters high this succeeds.)

• The higher the speed of the ball that you throw, the more surprising the demonstration. But to do this, practicing is absolutely necessary. (But when you miss, this enlightens your performance in front of your students and their laughing will consolidate their reminiscence of this demonstration.)

• When you are able to keep the ball between the floor and the table (two horizontal surfaces), then the thrown ball goes to and fro quite a number of times, and eventually moves only up and down perfect vertically. The same can be tried between two vertical surfaces: the ball thrown will go up and down a number of times. So, in these two cases an oscillating displacement of the ball can be observed (see the article in AJP 72-7). When you try these possibilities the ball needs to be thrown at very high speeds.

• Many other strange bounces are possible: see Boomerang ball.

Sources¶

• Walker, J., Roundabout, the Physics of Rotation in the Everyday World, pag. 8-12

• American Journal of Physics, pag. 875-883 (Vol.72-7; 2004)

• Nederlands Tijdschrift voor Natuurkunde, 70/10(2004), pag. 347

• McComb, W. D. Dynamics and Relativity, pag. 3