06 Sleeper

Aim¶

To show how a spinning top rises itself to a vertical spin

Subjects¶

• 1Q60 (Rotational Stability)

Diagram¶

Equipment¶

• Small top

• Top with felt-pen

• Bicycle wheel with handles, the handles fixed

• Hard surface to spin the tops on

• White standard hardboard (about $50 \times 50 \mathrm{~cm}^2$)

Presentation¶

• Spin the small top with a quick snap of your fingers, in such a way that the top starts spinning having its spinning axis make a quite large angle with the vertical. The top runs in an arc and very soon stands vertically upright. When disturbing this upright position the vertical position returns very quickly; the vertical position appears to be very stable.

• Take the top with the felt-pen and spin this top with a quick snap of your fingers on the white hardboard. This top will move in the same way as the small top we started the demonstration with, but now it traces the way the top moves because it is drawing its track on the white hardboard. We see that the top moves in a converging spiral, meanwhile lifting itself to the vertical. (See Diagram. In this figure the spiral moves to the right, because the board is not completely horizontal.)

When the top slows down, it increases its angle with the vertical and finally topples down (see the last part of the track in Diagram).

• The same demonstration as the foregoing can be done with a bicycle wheel with handles, having the handles fixed to the wheel. The handles should be smoothly rounded and the bicycle wheel should be carefully dynamically balanced. With this bicycle wheel the same observations can be made as with the foregoing demonstrations. However, one observation can be added: When finally the bicycle wheel spins with its axis vertical, after some time it will slow down and the spinning axis moves away from the vertical but then suddenly the supporting handle slips strongly and immediately the spinning wheel lifts itself again. This repeats itself a number of times until finally the wheel topples. (When the bicycle wheel is spinning on a table you can also hear the moments the wheel slips strongly. Then this sound is immediately accompanied with the lifting to the vertical of the bicycle wheel.)

Explanation¶

The top, being almost a free body, moves around its centre of mass (CM), which remains stationary.

Due to its tilted position, the spinning top will precess ( $I_{0} \omega_{0}$ moves into the direction of gravitational torque $T_{p}$, see Figure 2a.).

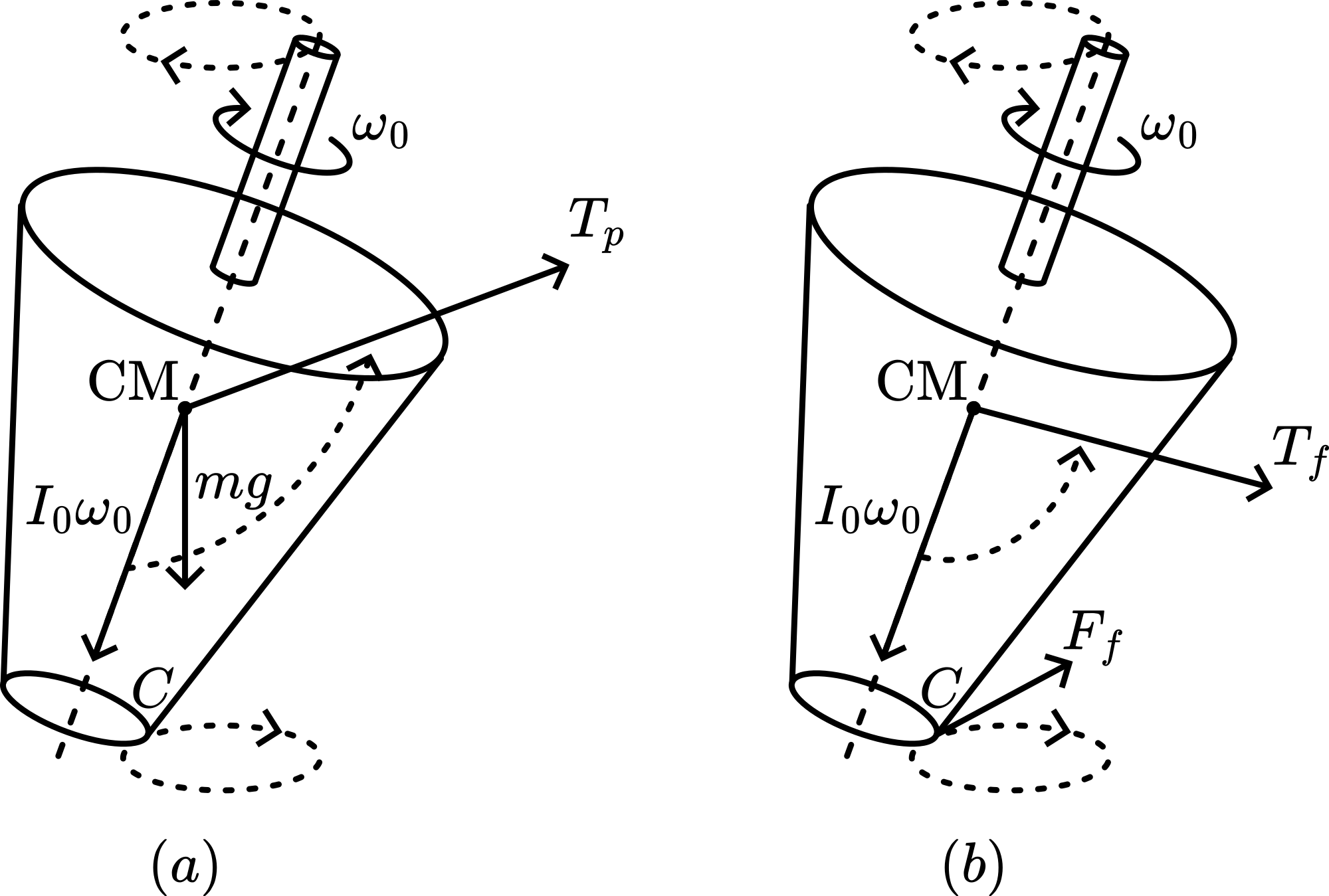
As a result the rounded stem of the top is attempting to roll over the floor in two ways: one due to the spin of the top around its body-axis and the other due to precession driving the stem over the floor. The first way is much faster than the second and so the rounded stem slips: it slips into the direction of spin. The friction force on the stem in point $\mathrm{C}$ is opposite to the slip, so friction is directed backwards (see Figure 2b). The torque of this friction force ( $T_{f}$ ) is almost perpendicular to $I_{0} \omega_{0}$, so $I_{0} \omega_{0}$ continues to rise until the top is positioned vertical ( $T_{f}$ will tend to align $I_{o} \omega_{0}$ ). The orientation of the top follows that of $I_{0} \omega_{0}$, and the top rights itself.

Once perfectly vertical the friction force is no longer present, but any disturbance moving the top away from the vertical immediately introduces a raising torque again, restoring its vertical position.

While moving to the vertical the track of precession will have a smaller radius of curvature, so while raising, we will see a converging spiral ending in a point.

Due to dissipation the spin of the top is slowed down and a point will be reached when slipping stops. Consequently the raising torque is no longer present: the top topples.

Remarks¶

• Tops having a large radius of curvature have more trouble to rise to the vertical. (They loose too much energy while slipping before reaching the vertical.)

• When you have enough experience throwing the top with the felt-pen you can make it turn on an overhead-projector, so a large group of students can see the spiral-movement.

• See also the demonstrations Precession 3a and Precession 3b in this database where it is shown how a precessing object reacts to an applied torque.

Sources¶

• Borghouts, A.N., Inleiding in de Mechanica, pag. 230-232

• Friedrich, Artur, Handbuch der experimentellen Schulphysik, part 2, Mechanik der festen Körper, pag. 233-234

• Roest, R., Inleiding Mechanica, pag. 230-231