8. Inleiding gebruik oscilloscoop#
8.1. Doel#
8.1.1. Practicumdoel#
Het practicumdoel is de karakteristieken van een RC-circuit te bepalen.
8.1.2. Leerdoel#
De oscilloscoop is een zeer veel gebruikt universeel meet- en testinstrument. Als (experimenteel) fysicus is het dus van belang dit instrument goed te kennen. Het doel van deze proef is het leren gebruiken van de basis mogelijkheden van een 4-kanaals oscilloscoop - waarbij we slechts 2 kanalen gebruiken. Hieronder vallen AC/DC-koppeling, gevoeligheid, tijdbasis, triggering (niveau en helling), tweekanaalsgebruik en fase. Je leert de diverse mogelijkheden van het instrument kennen aan de hand van metingen aan een RC-circuit en aan een LED.
De uitwerkingen van de opdrachten, zoals gemeten en berekende getalwaarden, grafieken, argumenten, etc. moeten tijdens het experimenteren overzichtelijk in je laboratoriumjournaal worden genoteerd, zodat over deze proef, wanneer gewenst, een verslag kan worden geschreven.
Tip
Labjournaal De voorbereidingsvragen die hieronder staan, vind je ook in je labjournaal gebundeld. Maak gebruik van het labjournaal voor het beantwoorden van deze vragen.
De metingen aan het RC-circuit kunnen gebruikt worden bij de tweedejaarsvakken Elektronische Instrumentatie en bij Systemen en Signalen. Aan het eind van het practicum, op de dag zelf, lever je het (digitale) labjournaal in op BS en laat je deze aftekenen bij de TA voor beoordeling.
Fig. 8.1 De te gebruiken oscilloscoop in dit practicum#
8.2. Voorbereiding#
Voor meer achtergrond over condensatoren, zie het betreffende hoofdstuk van elektromagnetisme en AC-schakelingen. Lees onderstaande tekst en maak alle opdrachten.
8.2.1. Signalen meten#
In de natuurkunde zijn we vaak geïnteresseerd in het verband tussen twee grootheden, zoals de temperatuur als functie van de tijd, of hoe de stroom afhangt van de opgelegde spanning. Met een oscilloscoop kan dat verband direct zichtbaar gemaakt worden. Op een scherm wordt grafisch de gemeten grootheid weergegeven tegen de tijd of tegen een tweede grootheid d.m.v. een tweede ingangskanaal. Bij een oscilloscoop zijn de ingangssignalen altijd elektrische spanningen; wil je een andere grootheid (geluid, druk, temperatuur, lichtsterkte, veldsterkte, stroomsterkte, …) weergeven dan is een sensor als omzetter nodig.
De meeste signalen in de natuur zijn analoog van aard. Om een analoog meetsignaal in een geheugen op te slaan moet dit eerst gedigitaliseerd worden. Dat gebeurt met een Analoog-naar-Digitaal-Converter (ADC). De resolutie daarvan bepaalt de kwaliteit van het in het geheugen opgeslagen signaal: bij \(N\) bits wordt het beschikbare spanningsgebied \(U_{\text{mm}}\) voor het te meten signaal in \(2^N\) intervallen opgedeeld. Dit gebied moet zo worden gekozen dat het te meten signaal altijd binnen de grenzen van dit gebied blijft. Zo niet, dan kan het gedigitaliseerde signaal ernstig verminkt raken! De resolutie is dan: \({U_{\text{mm}}/2^N}\).
Een \(N=8\) bits ADC is zeer gangbaar in een digitale oscilloscoop (in de SoundBlaster is \(N=12\) tot \(14\) gangbaar, en in de DAC van een MP3-speler kan dat tot \(N=18\) oplopen). De te gebruiken oscilloscoop heeft een 12 bits ADC. De resolutie bepaalt dus de mate waarin je details in je signaal kunt meten. De resolutie wordt wel beperkt door de eis dat de ADC-conversie snel moet zijn: als we bijv. signalen van \(100 \; \mathrm{MHz}\) willen zien, dan moet (in principe) de ADC de omzetting doen in minder dan \(10 \; \mathrm{ns}\). Dat is niet eenvoudig als je ook een grote resolutie wilt. Niet eenvoudig vertaalt zich in ‘duur’. Op het practicum gebruiken we digitale oscilloscopen met \(N=12\) bits resolutie, zodat het verticale gebied op het scherm in \(2^{12} = 4096\) intervallen is opgedeeld.
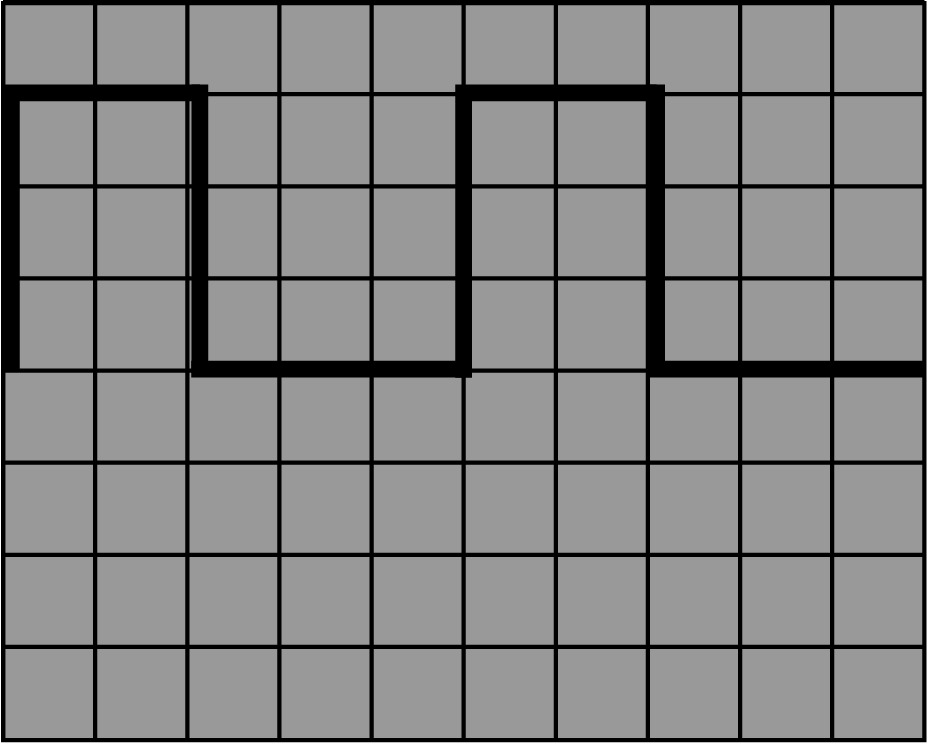
Fig. 8.2 Weergaven van een signaal op een oscilloscoop#
8.2.2. Oscilloscoop#
De te gebruiken Siglent SDS814X HD heeft een \(100 \; \mathrm{MHz}\)-bandbreedte, wat wil zeggen dat signalen met een periode van \(10 \; \mathrm{ns}\) gemeten kunnen worden. Bij het gebruik van een enkel kanaal wordt het tijdsafhankelijke signaal getoond. Dit houdt in dat de gemeten spanning op de verticale as staat en de tijd op de horizontale as. Met een 2-kanaals oscilloscoop kunnen twee signalen op verticale assen Y1 en Y2 tegelijk tegen dezelfde tijd as (X) worden weergegeven, zie onderstaand X-Y diagram. Daarmee is het mogelijk het tijdgedrag van de twee signalen te vergelijken, zodat bijv. de onderlinge faserelatie kan worden gemeten. De oscilloscoop kan ook in een speciale X-Y-mode worden gebruikt, waardoor de relatie tussen twee signalen kan worden bekeken.
In de digitale oscilloscoop wordt het weer te geven signaal eerst in een geheugen opgeslagen, en daarna op het scherm afgebeeld. Dat scherm is vaak een vloeibaar kristal display (LCD). Je kunt een aantal signalen opslaan en onderling vergelijken, of er berekeningen mee doen: verschillen nemen, vermenigvuldigen, integreren, middelen, etc. Je kunt de data in een computer verder bewerken of ze afdrukken.
8.2.3. Basisinstelling#
Om de eigenschappen van de te meten grootheid goed te kunnen bestuderen, zijn twee instellingen van groot belang: de verticale gevoeligheid en de tijdbasis. De verticale gevoeligheid is het ingestelde spanningsbereik in V/div (divisie, hokje). Op de te gebruiken oscilloscoop zijn dit de twee grote draaiknoppen. Links onderin staat de gevoeligheid voor de twee signalen (wanneer ingesteld) weergegeven. De tijdbasis is de instelling voor de tijd in s/div. Een kleinere tijdsbasis betekent dat een hogere frequentie van een signaal zichtbaar wordt.
Exercise 8.1
Op je oscilloscoopscherm zie je een periodiek pulsvormig signaal zoals hieronder.
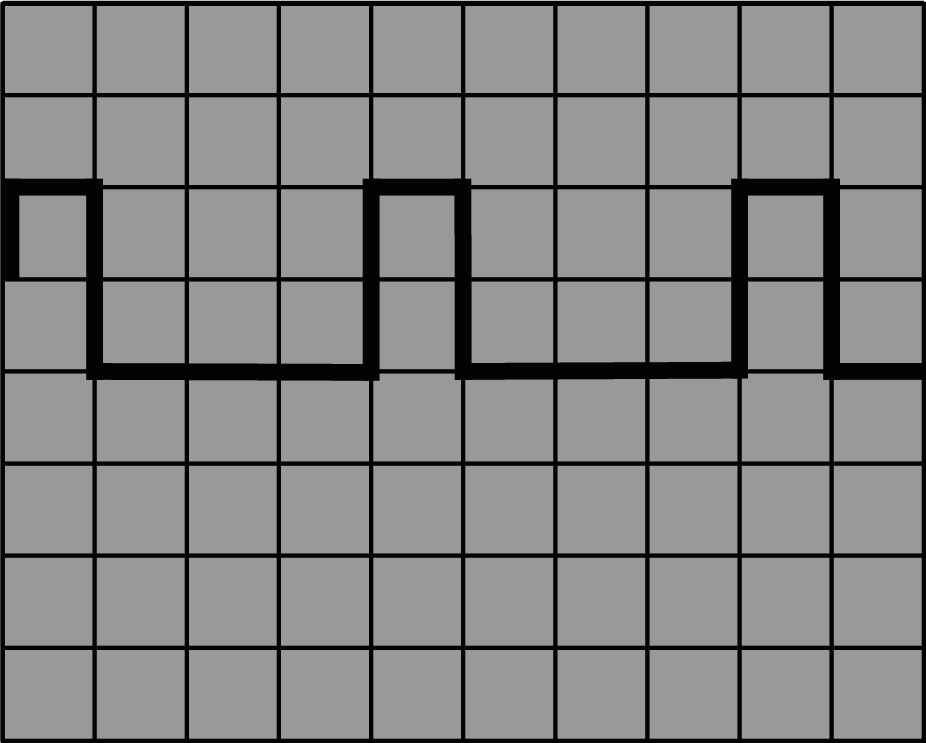
Fig. 8.3 Weergaven van een signaal op een oscilloscoop#
Bij de volgende instellingen:
Versterking: 2 V/div
Tijdbasis: 5 ms/div
Triggerhelling: +
Koppeling: DC
Bepaal de periode, de top-topwaarde en de pulsduur.
8.2.4. Triggeren#
Om een signaal goed uit te kunnen lezen, is het handig dat deze niet over het scherm ‘loopt’. Om het signaal altijd op hetzelfde punt te laten beginnen (in het midden of aan de linkerkant van het scherm), is het nodig om het signaal te triggeren. Het idee is dat de weergave pas weer start wanneer het signaal een van tevoren gedefinieerd punt bereikt, het triggerniveau of triggerlevel. Dat niveau kan vanaf boven of vanaf onderaf benaderd worden en moet dus ingesteld worden (slope+ of slope-).
Exercise 8.2
Op je oscilloscoopscherm zie je een periodiek pulsvormig signaal zoals hieronder.
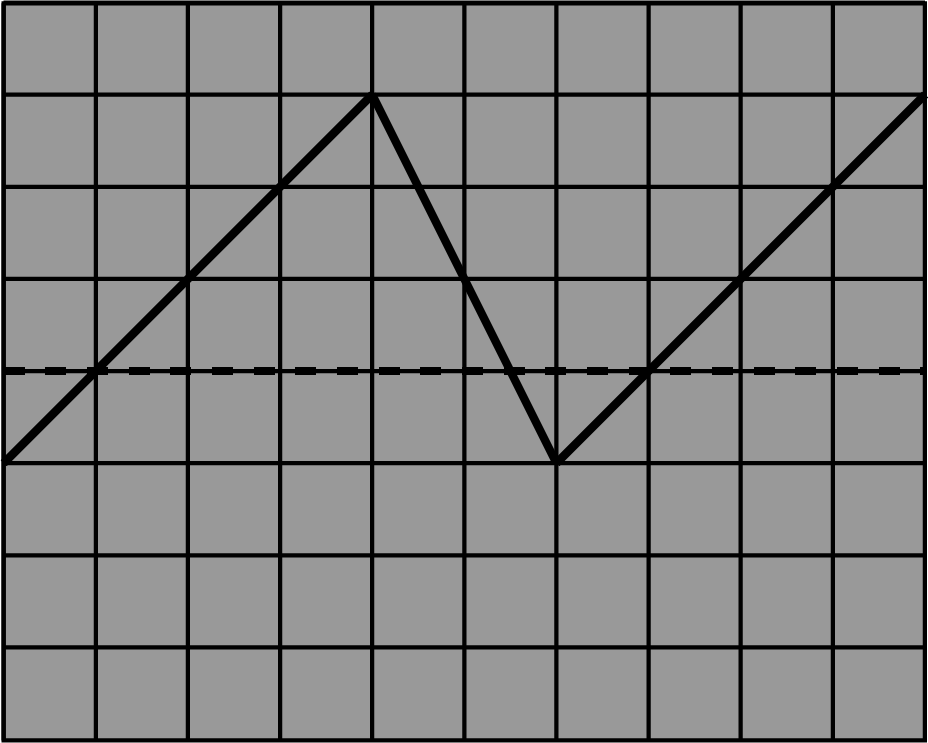
Fig. 8.4 Weergaven van een periodiek pulsvormig signaal.#
Teken hoe het signaal weergegeven in het figuur zal worden wanneer het signaal links verder gaat waar het rechts eindigt.
De verticale gevoeligheid staat ingesteld op 0.2 V/div. Teken hoe het signaal op het beeld er uit zal zien als het triggerniveau wordt ingesteld op 0.35 V, zowel voor slope+ als slope-.
8.2.5. Meten en rekenen#
Met de tijdbasis is het eenvoudig tijdsverschillen en daarmee faseverschillen, en frequenties te meten. Frequentie volgt direct uit het meten van het tijdsverschil tussen twee opvolgende gelijke punten (waarde en helling!) van het signaal: het tijdsverschil daartussen is de periode \(T\), zodat voor de frequentie geldt \(f = \frac{1}{T}\). Het meten van het faseverschil tussen twee signalen gaat op een vergelijkbare manier. Hiervoor is een twee-kanaals oscilloscoop nodig. Meet eerst (bijv. in aantallen divisies) de lengte van de periode van het signaal. Bepaal daarna de verschuiving (ook in divisies) van beide signalen t.o.v. elkaar. De verhouding levert de verschuiving op, in eenheden van de periode. Om dat naar graden om te rekenen volstaat vermenigvuldigen met \(360\).
Het voordeel van een digitale oscilloscoop is dat deze zelf metingen en berekeningen kan doen. Onder de knop MEASURE vind je diverse mogelijkheden voor metingen. De belangrijkste zijn TIME en daaronder FREQUENCY en VOLTAGE en daaronder Vpp. Het zelf aflezen van de periode en afleiden van faseverschuiving is daarmee onnodig geworden.
Exercise 8.3
Op je tweekanaalsoscilloscoop is onderstaand beeld zichtbaar van twee in fase verschoven sinusvormige signalen A en B. Daarbij is signaal A op ingang Y1 (of Ch 1) aangesloten en signaal B op ingang Y2 (of Ch 2).
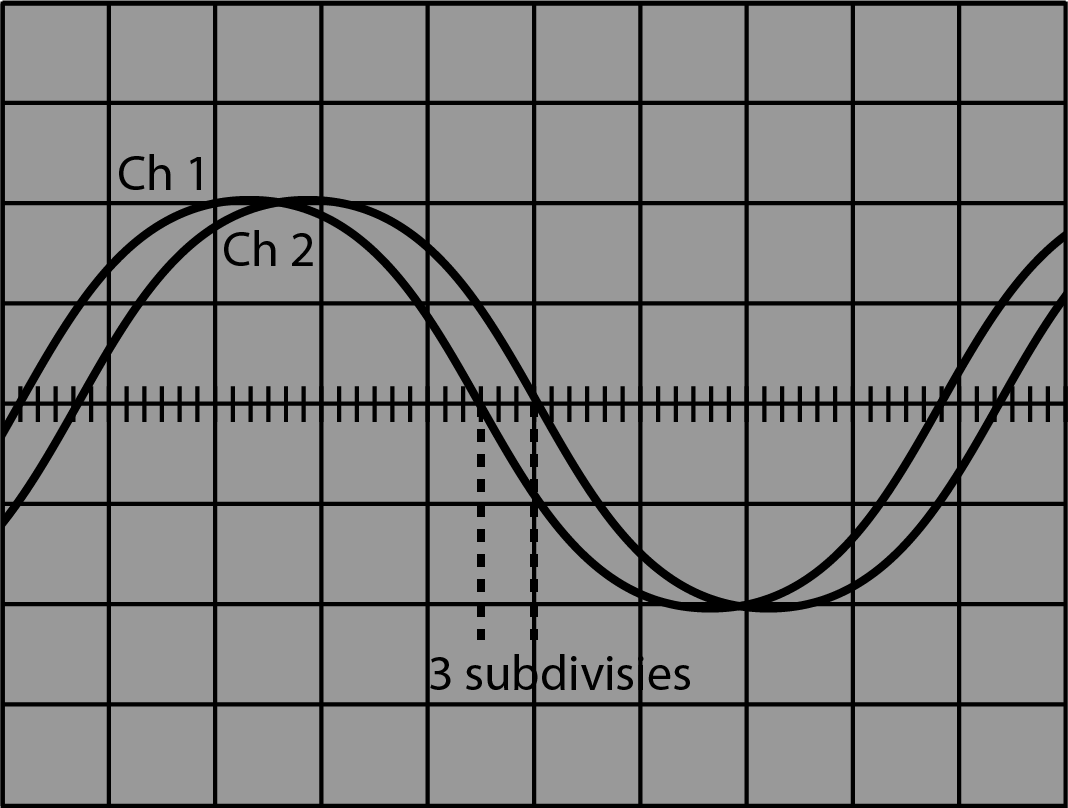
Fig. 8.5 Weergaven van twee periodieke signalen. Met de instellingen: Versterking: 1 V/div, Trigger: Kanaal Ch2.#
Geef aan welk signaal (Ch1 of Ch2) in fase vòòr loopt op het andere.
Bepaal het faseverschil in graden.
Wat is het ingestelde triggerniveau (in V)?
Wat is de ingestelde triggerhelling (+ of -)?
8.2.6. Koppeling van het signaal naar de schermafbeelding: AC, DC of GND#
Elk signaal kan worden geschreven als:
Er kunnen dus twee bijdragen worden onderscheiden: een gelijkspanning (of DC) \(V_1\) en een wisselspanning (AC) \(V_2\), die van de tijd \(t\) afhangt. De beide termen zijn zo gekozen dat voor de gemiddelde waarde van het wisselspanningsdeel geldt \(⟨V2(t)⟩ = 0\), \(⟨V⟩\) geeft aan het gemiddelde van \(V\). Anders gezegd: \(V_2(t)\) bevat geen DC, ofwel offset.
In veel gevallen zijn de amplitudes van beide delen sterk verschillend. Om beide delen goed te kunnen bekijken kan, met een schakelaar, de ingang Y op twee verschillende manieren intern worden verbonden naar de afbeelding op het scherm. In het eerste geval (DC-koppeling) wordt het hele signaal \(V(t)\) onveranderd doorgelaten. In het andere geval wordt alleen het AC-deel \(V_2(t)\) doorgelaten en afgebeeld: dit wordt aangeduid met AC-koppeling.
Zoals gezegd, is in de AC-stand per definitie de gemiddelde waarde van het signaal dat naar het scherm wordt doorgegeven gelijk aan nul. Dat betekent dat we direct aan de afbeelding kunnen zien of de koppeling op DC of AC staat: komt het gemiddelde van het signaal overeen met de nullijn op het scherm dan staat de koppeling op AC. Zo niet, dan is er een DC-component aanwezig, en staat de koppeling dus op DC.
Meestal is een derde stand van deze koppelingsschakelaar beschikbaar, waarbij het ingangssignaal volledig wordt onderdrukt, en een signaal \(V = 0\) wordt afgebeeld. Deze stand, met GD of GND (voor GrouND) aangeduid, maakt het mogelijk eventuele in de oscilloscoop aanwezige verschuivingen te compenseren. Dit gebeurt met de knop Y-pos. Deze instelling kan ook worden gebruikt om signalen met een relatief grote DC-bijdrage \(V_1\) meer gedetailleerd in de buurt van het maximum of minimum te kunnen bekijken. Overigens is ook voor de X-as een regelbare verschuiving aanwezig, X-pos geheten.
Exercise 8.4
Op je oscilloscoopscherm levert een periodiek pulsvormig signaal op. Als de ingangskoppeling (AC-GND-DC) op GND wordt gezet, is een vrijlopende horizontale lijn zichtbaar die samenvalt met de horizontale rasterlijn in het midden.
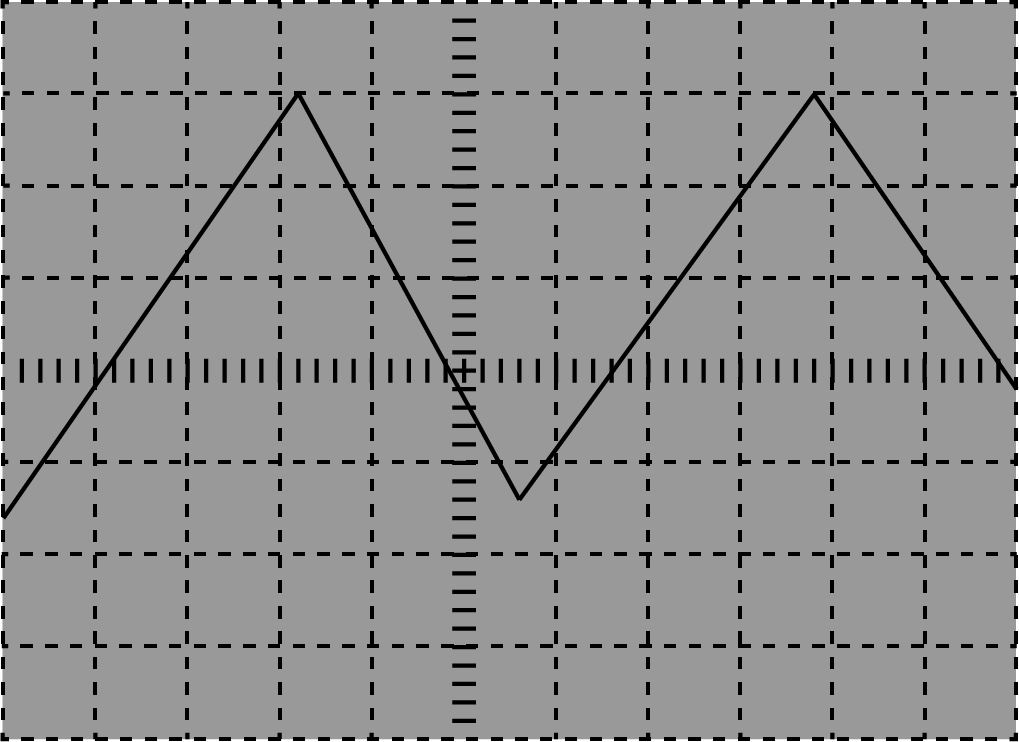
Fig. 8.6 Weergaven van een periodiek signaal. Met de instellingen: Versterking: 2 V/div, Tijdbasis: 5ms/div, Triggerhelling: +, Koppeling: DC#
Wat is het triggerniveau (in V)?
Wat is de periode van het signaal (in ms)?
Wat is de frequentie van het signaal (in Hz)?
Wat is de tijdsduur van de neergaande flank van het signaal?
Waaraan kun je zien dat de ingangskoppeling op DC staat?
8.2.7. Light Emitting Diode#
Een LED is een diode die licht geeft op het moment dat de spanning in de doorlaatrichting hoog genoeg is. Als de spanning in de andere richting staat, of als de spanning in doorlaatrichting onder de drempelspanning zit, dan blokkeert de LED de stroom. In de proef ter bepaling van de constante van Boltzmann wordt de werking van diodes uitgebreider uitgelegd, als je deze proef nog niet gedaan hebt is het verstandig het stuk over de \((I,V)\)-karakteristiek uit het hoofdstuk over de constante van Boltzmann door te nemen.
Exercise 8.5
We bieden een \(5.0 \; \mathrm{Hz}, 5.0 \; \mathrm{Vpp}\) wisselspanning aan voor een LED in serie met een \(220 \; \Omega\) weerstand. De drempelspanning van de LED is \(1.7 \; \mathrm{V}\).
Stel de vergelijking op voor de aangeboden (bron)spanning.
Programmeer de aangeboven spanning voor twee perioden en laat de grafiek tonen.
Programmeer de spanning over de weerstand als functie van de tijd en toon beide signalen in dezelfde grafiek.
Bereken hoeveel procent van een periode de LED stroom door laat.
Leg uit hoe je aan de hand van dit signaal de drempelspanning van de LED kunt bepalen.
Leg uit wat er gebeurt met de felheid van branden en hoe het gemeten signaal verandert als je een off-set spanning toevoegt.
8.3. Theoretische achtergrond#
Een condensator is niet veel meer dan twee metalen plaatjes die op een kleine afstand van elkaar zijn geplaatst. De capaciteit \(C\) van een condensator kan worden berekend als:
waar \(Q\) de in de condensator opgeslagen lading is en \(V\) de spanning over de condensator. Zodra een externe spanning over de condensator wordt gezet,laadt hij op. Om veilig op te laden is een (kleine) weerstand in serie vaak noodzakelijk om de stroom te beperken. Hoe verder de condensator is opgeladen, hoe meer elektronen zich ophopen op een van de platen, wat een tegenspanning produceert. Het opladen wordt dus lastiger naarmate de condensator voller raakt:
Wetende dat de stroom gedefinieerd is als:
kan de volgende differentiaalvergelijking worden afgeleid:
Wanneer een constante spanning over de condensator wordt gezet, kan de stroom door het RC-circuit beschreven worden als:
waar \(RC = τ\) de RC-tijd van het circuit wordt genoemd. Een RC-circuit zoals in dit experiment kan gezien worden als een simpele versie van een low-pass filter. Een condensator blokkeert laag-frequente stroom en laat hoog-frequente stroom door. Dit gedrag wordt gevat in de reactiviteit (schijnbare weerstand) van de condensator:
waar \(f\) de frequentie van een sinusvormig signaal is. De reactiviteit van een condensator bij lage frequenties is dus hoog. Maar aan het andere uiteinde van het spectrum, bij hoog-frequente stroom, zien we dat de condensator geen tijd heeft om op te laden voordat de polariteit om klapt. Vrijwel alle stroom blijft gewoon beschikbaar in het circuit en de spanning over de condensator neigt naar 0. De reactiviteit van een condensator bij hoge frequenties is dus laag.
Bij hoge frequentie zal ook een bekend fenomeen van condensatoren optreden: de spanning over de condensator loopt 90deg voor op de stroom door de condensator, en dus de stroom door het circuit. Zoals net vermeld, laadt een condensator op zolang er stroom loopt, en bij hoge frequenties is de condensator op elk moment zo goed als ontladen. Dat maakt dat de spanning over de condensator stijgt zolang de stroom positief is en pas weer zakt als de stroom negatief is. In andere woorden: de spanning is maximaal op het punt waar stroom precies door 0 kruist, een faseverschuiving van 90 graden. De precieze faseverschuiving verandert met de frequentie en de onderdelen in het circuit:
waar \(R\) de weerstand in het circuit is. De gain wordt dan gegeven door:
Exercise 8.6
Lees de sectie uit het dictaat dat gaat over de eigenschappen van de aansluitkabels.
8.4. LAB-opdrachten#
De LAB-opdrachten staan in het volgende hoofdstuk in het labjournaal zelf. De uitwerkingen van de opdrachten, zoals gemeten en berekende getalwaarden, grafieken, curve fitten, argumenten, etc. moeten tijdens het experimenteren overzichtelijk in dit (digitale) laboratoriumjournaal worden genoteerd, zodat over deze proef, wanneer gewenst, een verslag kan worden geschreven. In deze proef zijn een aantal opdrachten opgenomen.
Een introductie in begrijpen van AC-DC signaal.
Een introductie van de basisfunctionaliteit van een digitale oscilloscoop (opdracht aan de hand van een RC-circuit).
Cursorfunctionaliteit van een digitale oscilloscoop en het uitgebreider gebruik.
Het gebruik van het RC circuit met een ruis signaal.
Het bepalen van de karakteristiek van een LED.
8.5. Materialen#

Fig. 8.7 Het electronica boardje dat gebruikt wordt in het experiment, met rechts de schematische weergave van het board.#
8.6. Verdere achtergrond informatie#
8.6.1. Het aansluiten van apparatuur: aders, draden, kabels, connectoren#
Elektronische instrumenten en apparatuur moeten, om met elkaar te kunnen communiceren, in het algemeen onderling met kabels of snoeren worden verbonden. Soms kan dat ook anders, zoals via draadloze communicatie (WiFi, Bluetooth, optisch) of radiografische besturing. We concentreren ons hier op de overdracht via elektrisch geleidende verbindingen.
Om een signaal via een geleidende verbinding over te brengen zijn i.h.a. twee draden of aders nodig. Voor spanningen is dat nodig omdat spanning een potentiaalverschil is en als zodanig meetbaar is; voor stromen is dat nodig omdat stroom per definitie een gesloten lus vraagt, en dus aan- en afgevoerd moet kunnen worden. Soms kan één enkele draad voldoende zijn, als de “aarde” als referentie (bij spanningen) of terugvoer (bij stromen) kan worden gebruikt. In huis is aarde present in een geaard stopcontact. In dat stopcontract wordt “aarde” gevormd door de twee metalen stroken loodrecht geplaatst op de twee spanningsvoerende pennen, die aangesloten zijn op een goed geleidende verbinding naar de grond en het grondwater. Aarde is met name bedoeld voor veiligheid. Het gebruik van aarde voor signaaloverdracht is in de praktijk vrijwel altijd een slechte keus.
Een verbindingskabel bestaat uit twee hoofdelementen: de eigenlijke kabel (die meerdere onderling geïsoleerde draden/aders kan bevatten) en de aansluitdelen of connectoren. Voor permanente verbindingen stel je aan een connector heel andere eisen dan aan een verbinding die vaak los- en vastgemaakt moet worden. In de experimenten in het lab komen gemakkelijk (de-)monteerbare connectoren uiteraard veel voor. We bekijken de belangrijkste.
De eenvoudigste verbinding is de enkele koperdraad, uit veiligheidsoverwegingen meestal opgeborgen in een isolerende omhulling. In het lab kom je die tegen als de rode, zwarte, gele, groene, etc. meetkabels of meetsnoeren van verschillende lengte, typisch tussen \(50 \; \mathrm{cm}\) en \(2 \; \mathrm{m}\). Om onderlinge aansluitingen te maken gebruiken we de banaanklem en banaanstekker (figuur 14.8, links). Deze stekker heeft afmetingen afgeleid van de stekkerpennen van de gewone (niet-randaarde) stekker die je aan alle gangbare elektrische apparatuur in Nederland aantreft. De bijbehorende banaanklem is de tegenpool van de banaanstekker, net zoals het stopcontact dat is van de stekker. De meetsnoeren in het lab hebben meestal een banaanstekker aan beide uiteinden. Om een werkende verbinding tussen twee apparaten te maken zullen i.h.a. dus minimaal twee meetkabels nodig zijn.
Het is ook mogelijk om de twee draden samen te voegen. Dat is vooral handig als je altijd beide draden tegelijk verbonden of losgemaakt moeten worden. Dat is zo bij alle huishoudelijke apparaten: als je daar één van beide zou kunnen losmaken zou er een levensgevaarlijke situatie ontstaan omdat op de resterende verbinding nog steeds de netspanning (t.o.v. “aarde”) kan staan! Ook in het lab kan die wens of noodzaak bestaan. Een voorbeeld van een twee-aderige kabel is de coaxkabel (Figuur 8.8, midden). Daarin zijn de twee aders niet naast elkaar maar concentrisch t.o.v. elkaar gemonteerd: de ene ader, binnenader genoemd, is een gewone draad; de tweede ader (mantel of buitengeleider genoemd) is als een omwikkeling om de binnenader aangebracht, uiteraard met een kunststof isolatorlaag ertussen! De voordelen van deze coaxiale constructie t.o.v. twee naast elkaar liggende aders zijn vooral bij het transporteren en meten van heel kleine signalen dan wel signalen met een heel hoge frequentie. Dat laatste is zichtbaar in het soort kabel gebruikt voor je tv-aansluiting. Uiteraard vraagt een coaxiale kabelconfiguratie ook een coaxiale connector. Daarvan bestaan bijna oneindig veel soorten, maar voor onze experimenten gebruiken we de zeer gangbare BNC-connector (zie Figuur 8.8, rechts). De afkorting staat voor British Naval Connector of Bayonett Neill-Concelmann. De buitenkant van de connector is met de mantel van de coaxiale kabel verbonden, en de binnenpen met de binnenader. Dat betekent dat vrijwel altijd de configuratie zo moet worden gekozen dat de buitenkant spanningsloos is en dus met aarde is verbonden. Het is belangrijk je dat goed te realiseren bij het opbouwen van een schakeling: Verbind nooit de buitenkant van een coaxkabel met een spanningsvoerend punt! Je kunt ervan uitgaan dat in de experimenten binnen de serie Inleiding Instrumentatie bij alle BNC-aansluitingen op apparaten (generator, oscilloscoop, …) de buitenkant met de kast en de (rand-)aarde verbonden is.
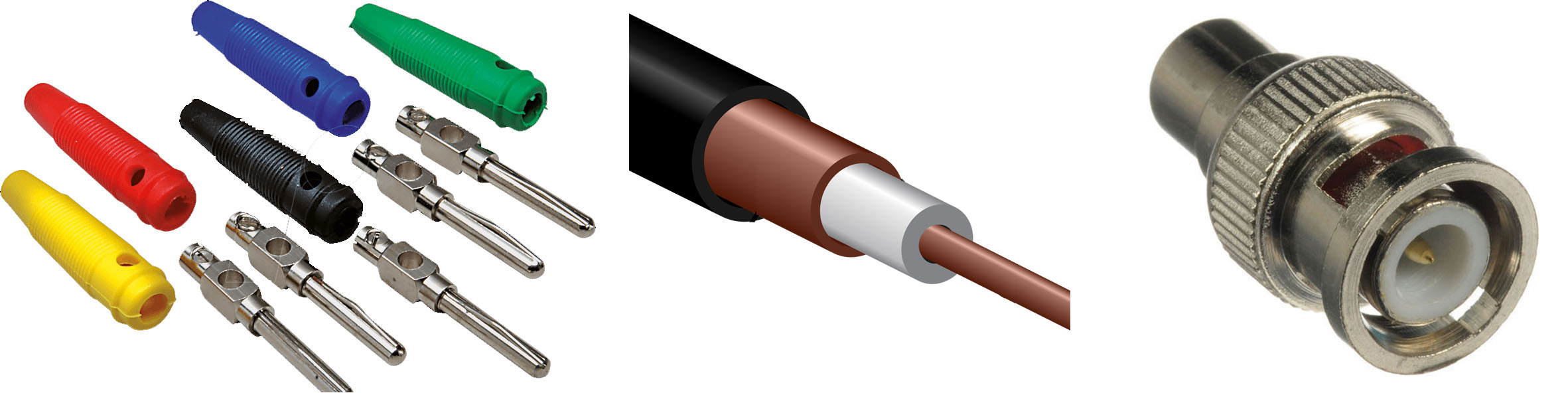
Fig. 8.8 Banaanste(k)kers; met een aangesloten draad wordt deze toegepast als de meest gebruikte methode voor het verbinden van instrumenten. De zijopening maakt het mogelijk een tweede banaanstekker in de eerste te plaatsen. Centraal een afbeelding van een coaxiale kabel, met de twee geleiders concentrisch geplaatst. Rechts een BNC connector, gebruikt bij coaxiale kabels.#
