15. Bepaling van de constante van Boltzmann#
15.1. Doel#
15.1.1. Practicumdoel#
In dit practicum ga je het \((I,V)\)-karakteristiek van een silicium diode bepalen. Je doet metingen aan hele kleine stroomsterktes. Je mag zelf bepalen of je de Boltzmann constante bepaalt, of de idealiteitsfactor van de diode.
15.1.2. Leerdoel#
Hoewel moderne DMM’s behoorlijk ideale meetinstrumenten zijn, moeten we bij metingen in een schakeling rekening houden met de mogelijkheid dat de meter de spanningen en stromen in de schakeling verstoort. Het doel van deze proef is leren omgaan met de Digitale Multimeters (DMM’s). Daarnaast leer je werken met spanningsdeler en bouw je een eenvoudig elektrische schakeling.
15.2. Voorbereiding (\(t\)=2h)#
15.2.1. De constante van Boltzmann en de diode karakteristiek#
De constante van Boltzmann is de evenredigheidsconstante die temperatuur en (thermische) energie aan elkaar koppelt volgens:
De constante van Boltzmann komt ook voor in de zogenaamde Boltzmann verdeling. De Boltzmann verdeling geeft de waarschijnlijkheid van de energie van een elektron aan als functie van de temperatuur (\(p_i \propto e^{-\frac{E_i}{kT}}\)). In een halfgeleider, zoals een diode, is de energie van de elektronen ook verdeeld volgens de Boltzmann verdeling, waarbij de gemiddelde energie van een elektron gelijk is aan \(k_BT\) (\(T\) is de absolute temperatuur en \(k_B\) is de Boltzmann constante).
Bij een diode is er sprake van een (energie)barrière waardoor elektronen niet vrij kunnen bewegen. De grootte van de elektrische stroom bij kleine spanningen over de diode hangt dan af van de hoogte van de barrière ten opzichte van de energie van de elektronen. De hoogte van de barrière wordt mede bepaald door de grootte van de voorwaartse spanning. Hoe hoger de voorwaartse spanning des te lager de barrière. Om dit principe beter te snappen, kun je de achtergrond informatie over halfgeleiderdiodes lezen. Deze stof is niet noodzakelijk voor de uitvoering van deze proef.
De Boltzmann verdeling van de energie van de elektronen en de aanwezigheid van een barrière wordt mooi tot uiting gebracht in een theoretische formule die het verband tussen de (voorwaartse) stroom door en spanning over een diode beschrijft. Het verband tussen de stroom (\(I_D\)) door, en de spanning (\(V_D\)) over de diode wordt gegeven door de exponentiële functie:
\(q\) is hier de lading van een elektron, \(-1.602*10^{-19}\) C, \(k_B\) is de Boltzmann constante, \(n\) is de idealiteitsfactor (hangt af van waar precies de recombinatie plaatsvindt; \(n = 2.0 \pm 0.1\) voor Si) en \(I_0\) is de sperstroom, de stroom die loopt als \(V_D\) sterk negatief wordt. Schematisch ziet de \((I,V)\) karakteristiek er op lineaire schaal uit als weergegeven in figuur 15.1.
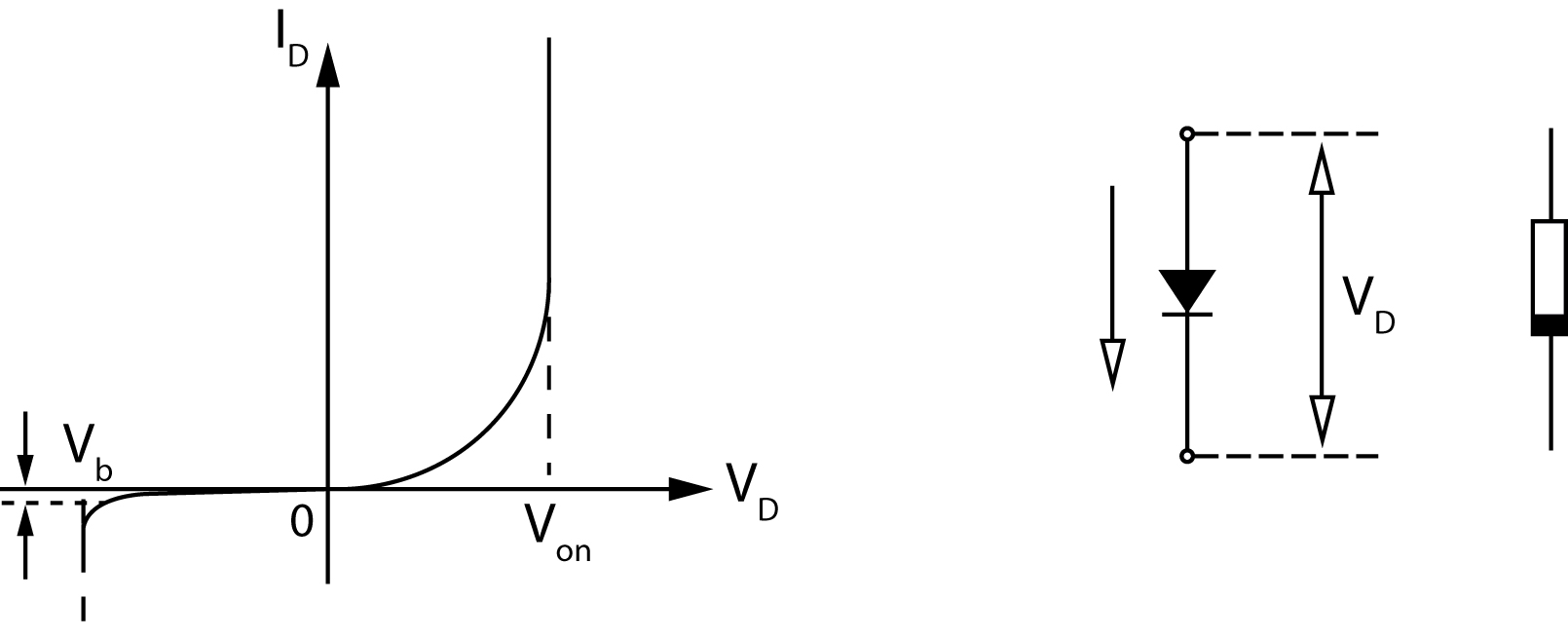
Fig. 15.1 Links: Diode karakteristiek (doorgetrokken lijn), vereenvoudigde diode karakteristiek (gestreepte lijn). Rechts: het standaard symbool voor een diode met voorwaartse stroom. Geheel rechts: Een donker randje op een diode geeft de aansluiting met het n-type gebied aan.#
In figuur 15.1 zien we ook dat bij zekere negatieve spanning \(V_b\) de stroom plotseling sterk toeneemt. Dit noemen wij de breakdown spanning van de diode. De diode gedraagt zich dan bijna als een kortsluiting. Dit gedrag wordt niet beschreven door vergelijking (15.1). Wat er gebeurt, is dat de spanning over het gebied zonder vrije ladingsdragers zo groot wordt dat de elektronen van de atomen worden ‘losgetrokken’ en als er één gaat, gaan er meerdere (lawine effect).
Maken we een plot van vergelijking (15.1) waarbij we de \(^{10}\)log van \(I_D\) uitzetten tegen \(V_D\) dan vinden we de doorgetrokken kromme in figuur 15.2.
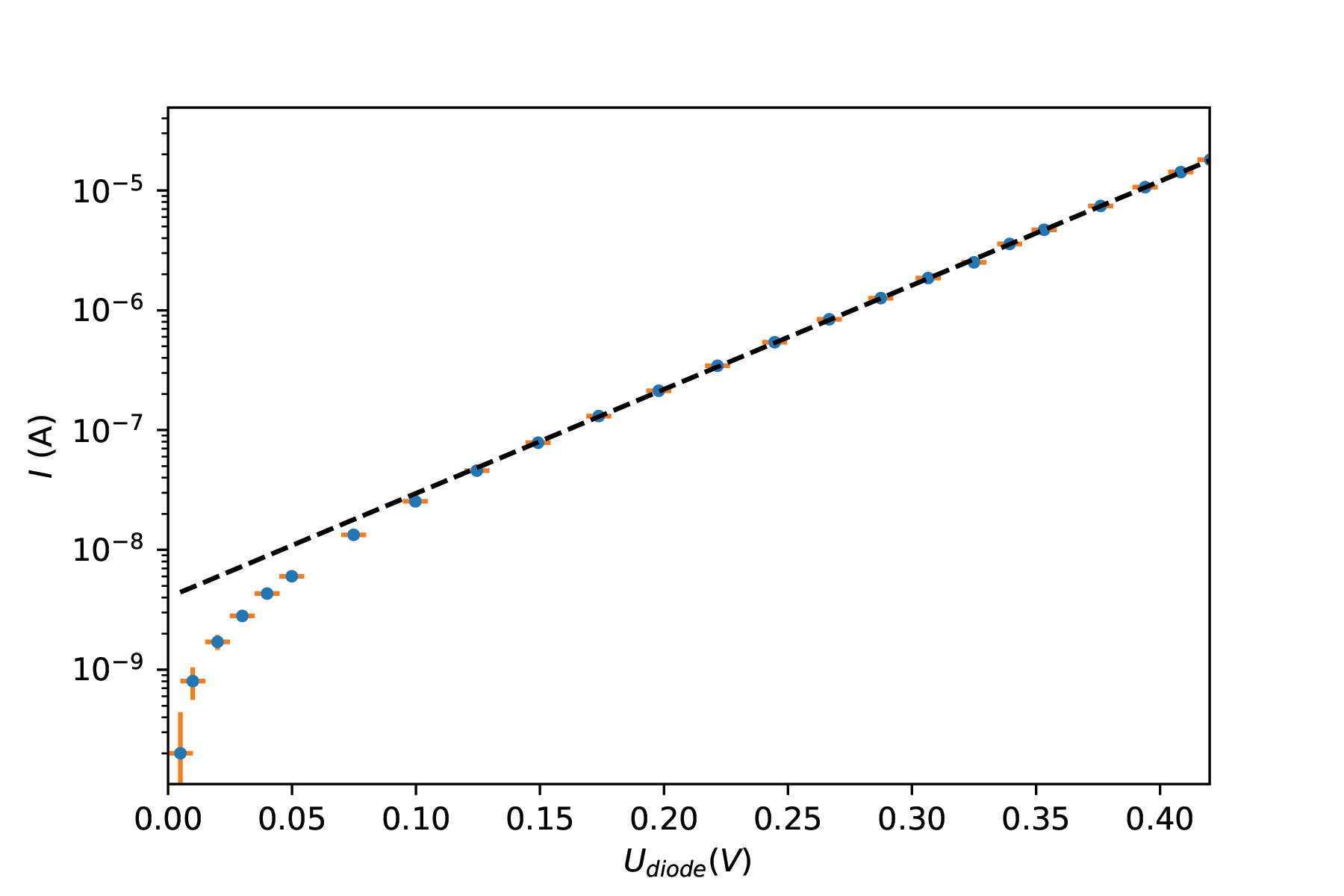
Fig. 15.2 (\(I,V\))-karakteristiek van een halfgeleiderdiode op semi-log schaal. De meetpunten volgen vgl. (15.1). De gestreepte lijn wordt verkregen door de “-1” in vgl. (15.1) weg te laten. Grafiek mogelijk gemaakt d.m.v. dataset van eerstejaars studenten uit 2019.#
We zien voor \(V_D>0.1 \)V een rechte lijn. Dit wordt veroorzaakt door het volgende. Voor het genoemde spanningsgebied is \(e^{\frac{-q V_{D}}{n k_{B} T}}>>1\). De stroom door de diode wordt in dat gebied dan ook goed beschreven met
Nemen we nu links en rechts de logaritme van deze vergelijking dan wordt dit
Dit is gelijk aan een vergelijking van een rechte lijn \(y=cx+d\). Deze vergelijking kun je gebruiken om de constante van Boltzmann te bepalen op basis van een handgemaakte grafiek. Echter, met de rekenkracht van de huidige computers is er geen goede reden te bedenken waarom te functie fitten op basis van het gehele domein, en dus op basis van vergelijking (15.1).
Tip
De afsnijding met de y-as geeft \(d\) en dus \(I_0\). Deze waarde kan handmatig bepaald worden en als initiële schatting (p0) in Python meegegeven worden.
Willen we de Boltzmann verdeling nader bestuderen, of een eigenschap (bijvoorbeeld de idealiteitsfactor) van de diode bepalen, dan is het dus de bedoeling dat we de sterkte van de stroom als functie van de spanning over de diode bepalen. Zowel het meten van een stroom als het meten van een spanning kan met een digitale multimeter (DMM).
15.2.2. Metingen met DMM’s#
Digitale multimeters zijn veelzijdige meetinstrumenten die onder meer gebruikt worden voor het meten van spanning, stroom en weerstand. Bij geavanceerdere modellen kun je de DMM met een computer besturen en uitlezen en frequenties, tijdsintervallen, capaciteiten, inducties, continuïteit, temperatuur, diode info etc. meten.
In deze proef beperken we ons tot gelijkspannings-, gelijkstroom- en weerstandsmetingen. Het is van belang je te realiseren dat het hart van een DMM wordt gevormd door een Analog Digital Convertor (ADC). Deze eenheid zet een getal op zijn display dat evenredig is met de spanning die op de ingang wordt aangeboden. Het bereik waarbinnen de ADC werkt, is meestal gelijk aan het gevoeligste bereik van de DMM voor gelijkspanningsmetingen (b.v. \(-100\)mV tot \(+100\)mV). Als we de meter op een minder gevoelig meetbereik zetten, schakelen we verzwakkers in die de ingangspanning reduceren tot in het bereik van de ADC. Dit is schematisch in Figuur (15.3) links weergeven. Om spanning met een DMM te meten gebruiken we de ingangen V en com of hi en lo.
Als wij een gelijkstroommeting uitvoeren, gebruiken wij de ingangen I of mA of A en com of lo. We meten bij een gelijkstroommeting in feite de gelijkspanning over een weerstand \(R_s\) (zie figuur 15.3 links onder). \(R_s\) wordt de shunt weerstand genoemd omdat daar de stroom doorheen loopt en niet door de rest van de meter. Deze weerstand kunnen we beschouwen als de inwendige weerstand van de stroommeter. In de laagste stroombereiken is \(R_s\) van de orde 100 \(\Omega\) tot 1000 \(\Omega\).
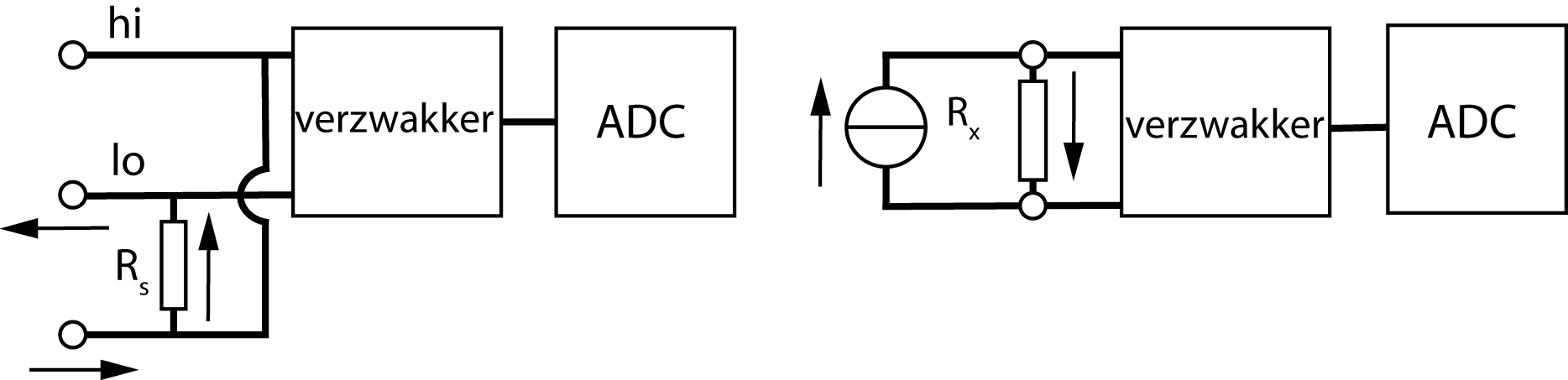
Fig. 15.3 Principe van gelijkspanning, gelijkstroom en weerstandsmeting met een DMM.#
Als we met de DMM weerstandswaarden meten, wordt er met behulp van een interne stroombron een stroom door de weerstand gestuurd en wordt de spanning over de weerstand gemeten (figuur 15.3 rechts). De grootte van de meetstroom wordt opgegeven in de handleiding van de DMM. Voor de laagste weerstands-bereiken is bijvoorbeeld 1 mA een typische waarde.
Note
De schema’s in figuur 15.3 zijn min of meer equivalente schema’s. Met name voor weerstandsmetingen bestaan veel variaties.
Bij het aansluiten van DMM’s moeten we ons ervan bewust zijn dat, zoals in figuur 15.3 links al is aangegeven, voor stroommeting heel vaak een andere ingang wordt gebruikt dan voor spannings- en weerstandsmetingen. In figuur 15.4 zijn de ingangen van een aantal DMM’s zoals wij die op het practicum gebruiken weergeven. Links de Dynatek D9100, \(3\frac{1}{2}\) digit DMM, in het midden de \(5\frac{1}{2}\) digit Thurlby 1905a en rechts de \(6\frac{1}{2}\) digit Agilent 34401A.
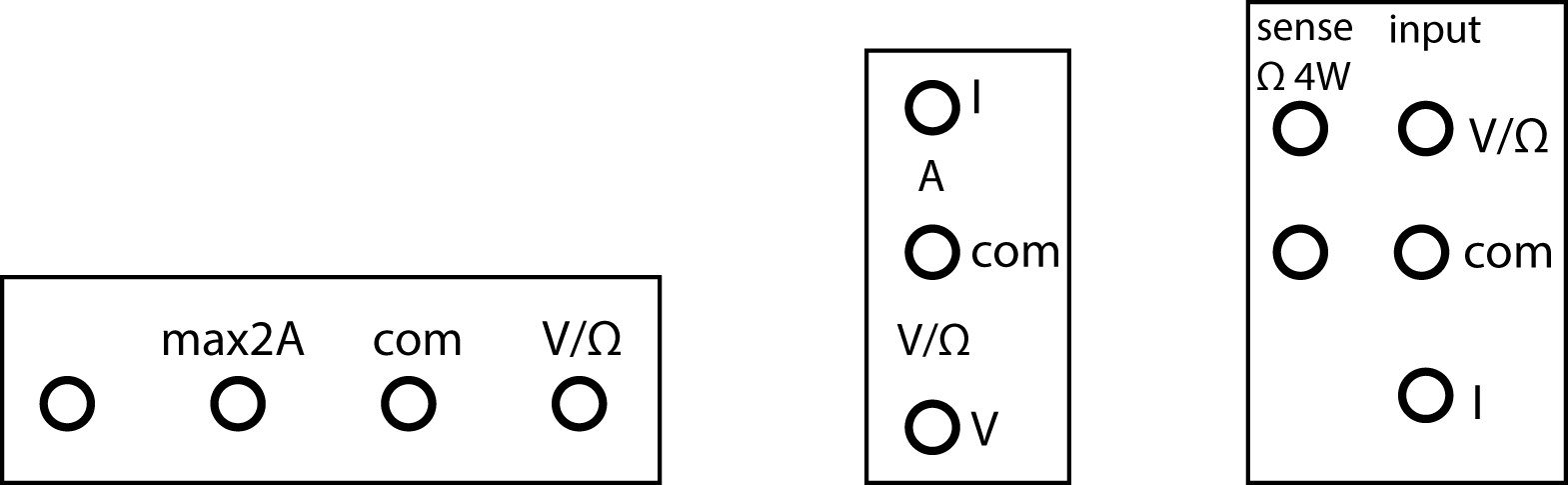
Fig. 15.4 Aansluitingen voor (van links naar rechts) de Dynatek, Thurlby en Agilent DMM.#
Warning
De kans is zeer groot dat, als wij van stroommeting overgaan op spanningsmeting (van b.v. een voedingsbron) en vergeten de draad uit de I-ingang naar de V-ingang te verplaatsen, op z’n minst de zekering voor de weerstand \(R_s\) (zie figuur 15.3 links) wordt opgeblazen. Let hier op!
15.2.3. Nauwkeurigheidspecificaties van een digitale meter#
We zouden kunnen veronderstellen dat de nauwkeurigheid van een meter bepaald wordt door een tel van de laatste decimaal van de uitlezing. Zo simpel is het meestal niet. Een fabrikant geeft de nauwkeurigheid van een DMM meestal op in \(\pm\)(..% aflezing + ..% bereik) of zelfs \(\pm\)(..% aflezing + ..% bereik + ..tellen (counts, digits)). Deze manier om de nauwkeurigheid op te geven is redelijk als we bedenken dat het verband tussen de ingangsspanning en wat er op de uitlezing staat in hoge mate lineair is (\(V_{\text{uit}} = aV_{\text{in}} + b\)). Fouten in \(V_{\text{uit}}\) kunnen dan goed gespecificeerd worden door fouten in \(a\) en \(b\) op te geven. De specificatie +% aflezing correspondeert met de nauwkeurigheid van de “gain” (= versterking) \(a\) en de aanduiding +% bereik + .. tellen correspondeert met de “offset” (= afsnijding) \(b\), die in het ideale geval precies nul is (zie figuur 15.5).
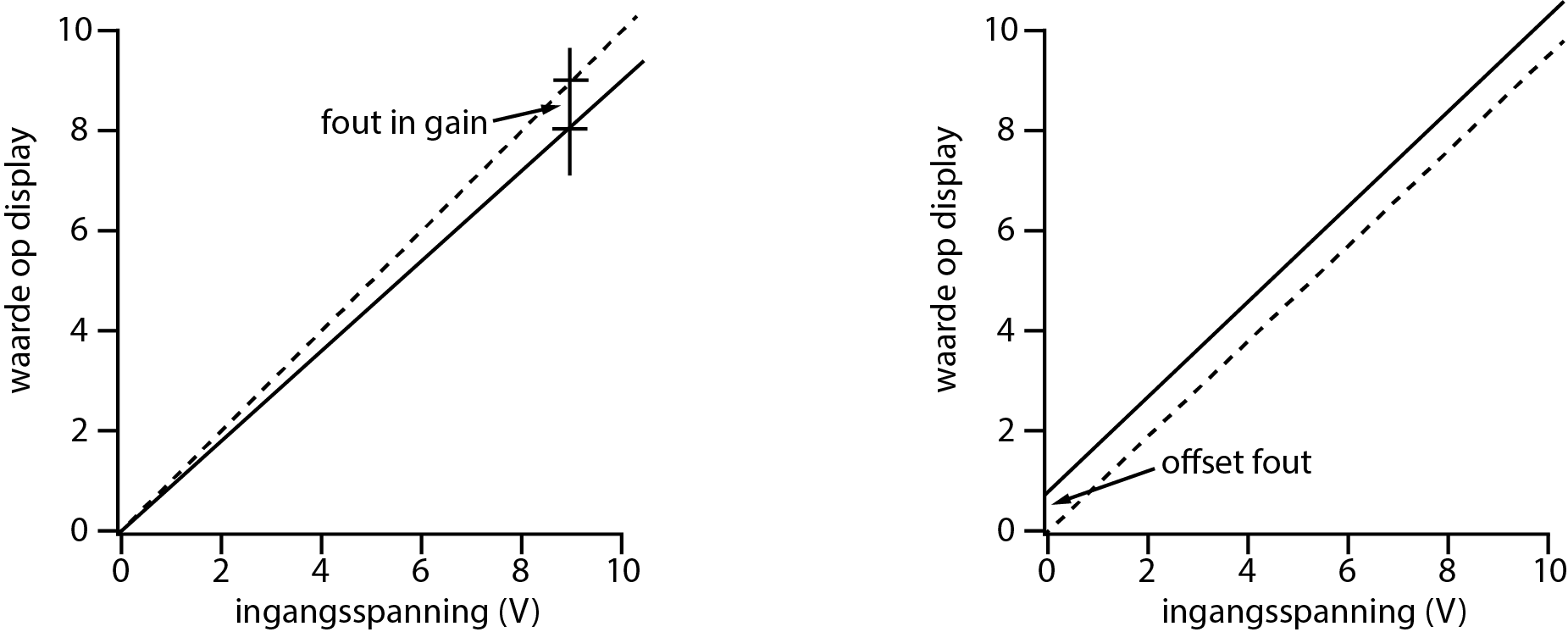
Fig. 15.5 De nauwkeurigheid van een DMM wordt opgegeven door de nauwkeurigheid van de helling (gain) en de afsnijding (offset) van het (veronderstelde) lineaire verband tussen de ingangsspanning en de waarde op het display op te geven.#
Voorbeeld
Stel we lezen af: 1.234 V op de 3\(\frac{1}{2}\) cijfer DMM. Hieruit mag je dus niet zomaar afleiden dat de nauwkeurigheid van de meting beter dan 1 mV is. Voor de Dynatek D9100 wordt voor het 2 V bereik opgegeven: \(\pm(0.5\%\) van de aflezing +1 tel). Dus: 0.5% van de aflezing is 6 mV. Plus 1 mV van het digit geeft dus een nauwkeurigheid van 7 mV . Het resultaat van de meting is 1.234\(\pm\)0.007 V. Nauwkeurigheid wordt ook vaak opgegeven in ppm (parts per million, 1% = 10000 ppm).
De resolutie van een digitaal instrument is de verhouding van het kleinste aantal tellen tot het grootste aantal tellen dat op het display kan worden weergegeven. Dit wordt in feite bepaald door het aantal tellen (counts) dat kan worden weergegeven en dat aantal hangt natuurlijk af van het aantal cijfers. Een simpele DMM heeft vaak \(3\frac{1}{2}\) cijfers. Dit betekent 3 hele cijfers (elk met waarden van 0 tot en met 9) plus een half cijfer dat de waarden 0 of \(\pm1\) kan aannemen. Dus een \(3\frac{1}{2}\) cijfer display kan 0 tot 1999 weergeven, totaal 2000 tellen. De resolutie van die DMM is 1/2000 of wel 0.05%.
Tip
Je werkt tijdens het practicum met een \(6\frac{1}{2}\) DMM. Deze zal je echter wel op deze resolutie moeten zetten. De standaard instelling is \(5\frac{1}{2}\).
De gevoeligheid bij een meting is de kleinste verandering van het te meten signaal die kan worden waargenomen. Een gevoeligheid bij een meting van 1 \(\mu\)V impliceert dat veranderingen in het signaal kleiner dan 1 \(\mu\)V niet kunnen worden waargenomen. De gevoeligheid hangt mede af van de grootte van het signaal dat we willen meten. Immers, de grootte van het signaal bepaalt het gevoeligste meetbereik waarop gemeten kan worden.
Voorbeeld
Stel we willen een spanning van ongeveer 15 V meten met een 3\(\frac{1}{2}\) cijfer DMM. Het gevoeligste bereik waarop we deze spanning kunnen meten, is het 20 V bereik. De kleinste verandering van het signaal die kan worden waargenomen is dan 10 mV (ga na). Voor een 5\(\frac{1}{2}\) cijfer DMM is dit 0.1 mV. Met een 3\(\frac{1}{2}\) cijfer DMM kun je ook een gevoeligheid van 0.1 mV halen, maar dan alleen voor signalen kleiner dan 200 mV. De ultieme gevoeligheid van een meetinstrument hangt af van zijn resolutie en het laagste meetbereik. Bijvoorbeeld de gevoeligheid van een 6\(\frac{1}{2}\) cijfer DMM met een laagste meetbereik van 200 mV is 0.1 \(\mu\)V.
15.2.4. Gebruik van DMM’s in een schakeling; ideale en niet-ideale spannings- en stroommeters#
Bij metingen in een schakeling is het van belang dat de DMM de stromen en de spanningen in de schakeling niet beïnvloedt. Het zal van de meter en de schakeling afhangen of er wel of niet significante beïnvloeding plaatsvindt. Om dit probleem op een systematische manier aan te pakken is het zinvol het concept van ideale spannings- en stroommeters te introduceren. Het spreekt vanzelf dat we een meter ideaal noemen als het plaatsen van de meter in een schakeling geen enkele invloed heeft op de eigenschappen (spanningen en stroomsterktes) van het circuit.
Bij het meten van de spanning tussen twee punten wordt de meter parallel gezet met een deel van de schakeling. Loopt er door de meter geen stroom, dan worden de stromen (en daarmee de spanningen) in de schakeling niet beïnvloed door de meter. Een ideale spanningsmeter is dus een meter waardoor geen stroom loopt. Wij kunnen ook zeggen: een ideale spanningsmeter heeft een oneindig hoge weerstand (zie figuur 15.6 meest links).
Door een niet-ideale spanningsmeter loopt dus wel stroom, de weerstand tussen de twee aansluitpunten is niet oneindig. Een niet-ideale spanningsmeter kunnen we representeren door een parallelschakeling van een ideale spanningsmeter en een weerstand (zie figuur 15.6 tweede figuur van links).
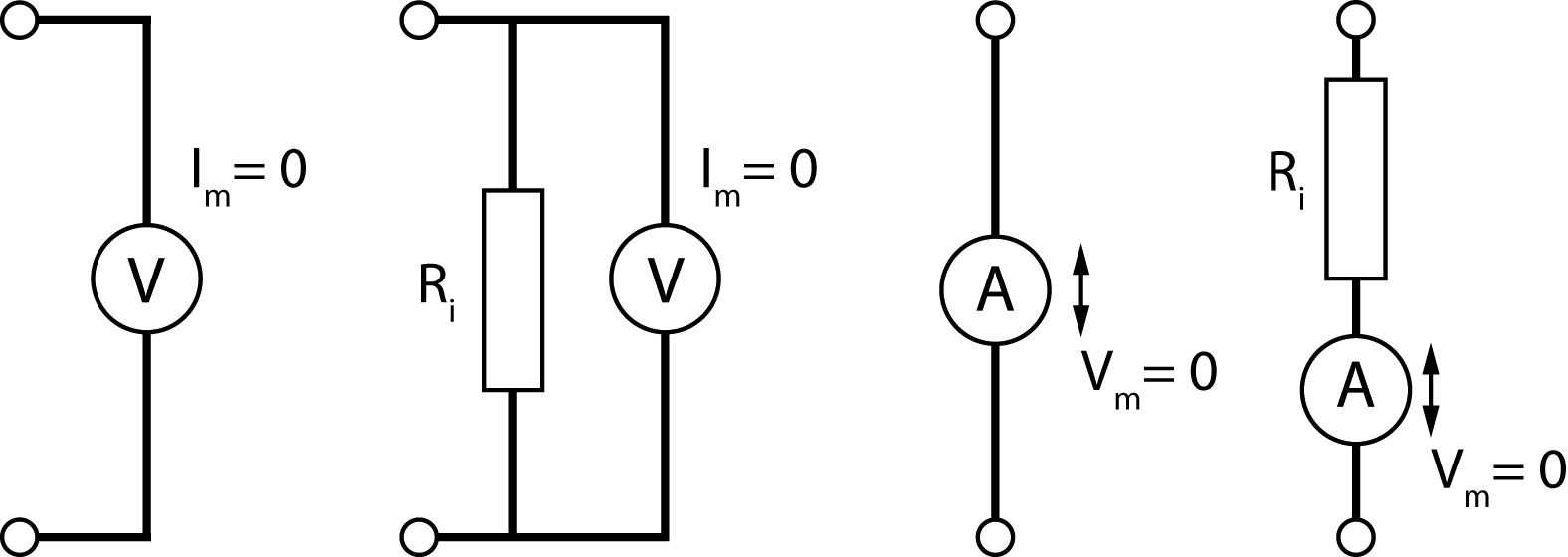
Fig. 15.6 Representatie van een ideale en niet-ideale spanningsmeter (links) en een ideale en niet-ideale stroommeter (rechts).#
Bij een stroommeting wordt de meter in een bestaande tak van de schakeling in serie met de al aanwezige elementen opgenomen. Valt er over de meter geen spanning dan worden de spanningen (en daarmee de stromen) in de schakeling niet beïnvloed door de meter. Een ideale stroommeter is dus een meter waarover geen spanning valt. Wij kunnen ook zeggen: de weerstand van een ideale stroommeter is gelijk aan nul (zie figuur 15.6 tweede figuur van rechts).
Over een niet-ideale stroommeter valt dus wel spanning en zijn weerstand is niet gelijk aan nul. Een niet-ideale stroommeter kan gerepresenteerd worden door serieschakeling van een ideale stroommeter en een weerstand (zie figuur 15.6 uiterst rechts).
De schema’s die het niet-ideale gedrag van de meters representeren zijn handig als we willen weten of de verstoring door de meters belangrijk is of niet. We zien bijvoorbeeld direct dat het meten van de spanning over een weerstand die in grootte vergelijkbaar is met de weerstand van de meter (\(R_{\text{i}}\)), tot verstoringen van de oorspronkelijke stroom/spanningsverdeling leidt. Zo zal een stroommeter verstorend werken als zijn weerstand (\(R_{\text{i}}\)) niet te verwaarlozen is ten opzichte van de andere weerstanden in de tak waarin de meter is opgenomen.
Voorbeeld
De spanning over een weerstand van 100 k\(\Omega\) wordt gemeten met een DMM met een weerstand van 1.0 M\(\Omega\). Beinvloedt de meting de eigenschappen van het oorspronkelijk circuit significant?
De DMM staat parallel aan de Ohmse weerstand. De vervangingsweerstand is gelijk aan: \(R_v = \frac{R_{DMM} \cdot R_O}{R_{DMM} + R_O}\) (ga zelf na!). De vervangingsweerstand is dus 91 k\(\Omega\)! Dat is inderdaad een significant verschil.
De verstoring door het aanbrengen van de DMM in een ingewikkelde, onoverzichtelijke situatie kan systematisch in beeld worden gebracht door de niet-ideale representatie van een spannings - of stroommeter in de schakeling te tekenen en de waarden van \(R_{\text{i}}\) in de handleiding van de DMM op te zoeken.
Moderne digitale multimeters hebben op het spanningsmeetbereik een zeer hoge interne weerstand (b.v. \(R_\text{i}\)=10 M\(\Omega\) of hoger). Bij stroommeting zijn deze meters in de lage bereiken iets minder ideaal (b.v. \(R_{\text{i}}\) = 1 k\(\Omega\)). Voor stroommeting wordt in de specificaties van een DMM \(R_{\text{i}}\) vaak niet direct opgegeven. Men specificeert de Voltage Burden: de maximale spanning die over de meter valt bij stroommeting. De weerstand van de stroommeter wordt dan vaak gegeven door (Voltage Burden) / (meetbereik).
Tip
Met behulp van de wet van Ohm kunnen we natuurlijk ipv de stroom gewoon de spanning meten over een Ohmse weerstand met bekende weerstandswaarde. Voorwaarde is natuurlijk dat die weerstand zelf de eigenschappen niet te veel verstoort.
Exercise 15.1
Voor de nauwkeurigheid van een DMM wordt voor het 10 V bereik opgegeven: 0.0015% van de aflezing en 0.0004% van het bereik. De spanning die wordt afgelezen is 5.00000 V. Wat is de nauwkeurigheid van de meting?
Wat is de gevoeligheid bij het meten van een gelijkspanning van ongeveer 9 mV met een 4\(\frac{1}{2}\) digit DMM op het 200 mV bereik?
# Jouw antwoorden
Exercise 15.2
Bekijk figuur 15.2. Leg uit waarom het direct meten van een stroomsterkte door de diode niet handig is.
Leg ook uit waarom het direct meten van de spanning over de diode niet nauwkeurig is. Denk aan het niet ideaal zijn van de meters.
# Jouw antwoorden
15.2.5. Spanningsdeler#
Om rekening te houden met het niet ideaal zijn van de meters, maken we in dit experiment gebruik van een spanningsdeler. In zijn eenvoudigste vorm is een spanningsdeler niets anders dan een serieschakeling van twee weerstanden. De (bron)spanning wordt dan gedeeld door de verschillende componenten in de schakeling. De vergelijkingen voor de stroomsterkte en de spanning staan als geheugensteuntje weergegeven in par. 15.4.1 van de achtergrondinformatie. Omdat de kennis van de spanningsdeler stof is wat in 4 VWO behandeld wordt, beschouwen we dit als voorkennis en wordt de benodigde kennis hieronder alleen getoetst.
Exercise 15.3
Stel we hebben een spanningsdeler bestaande uit een 330 \(\Omega\) en een 1000 \(\Omega\) weerstand. De maximale dissipatie in de weerstanden is 1 Watt.
Hoeveel stroom mag er door de 330 \(\Omega\) en door de 1000 \(\Omega\) weerstanden maximaal lopen?
Wij schakelen de weerstanden in serie. Hoeveel spanning mag erover de serieschakeling gezet worden zodat de maximaal toelaatbare dissipatie niet wordt overschreden?
Stel wij zetten 20 V over de serieschakeling. Bereken de spanning over de 330 \(\Omega\) weerstand en over de 1000 \(\Omega\) weerstand.
# Jouw antwoorden
Exercise 15.4
Bekijk figuur 15.7. Dit is de (basis)opstelling die gebruikt wordt in dit experiment.
Leg uit hoe de spanning over de diode bepaald wordt met behulp van deze schakeling.
Leg uit hoe de stroomsterkte door de diode bepaald wordt met behulp van deze schakeling.
Bepaal met behulp van bovenstaande twee methodes de onzekerheid in \(I_D\) en \(U_D\).
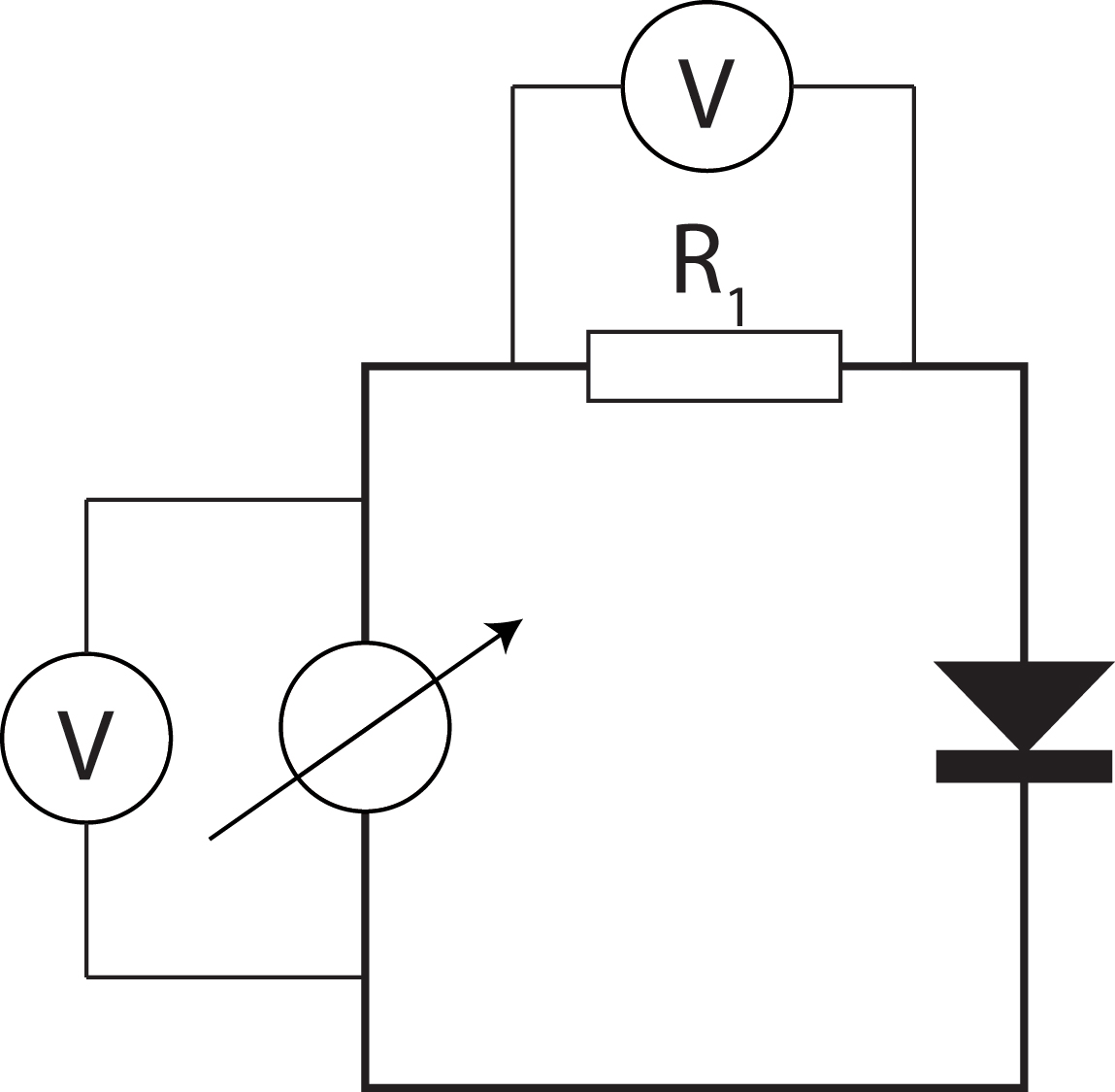
Fig. 15.7 De basismeetopstelling bestaat uit de diode en Ohmse weerstand in serie geschakeld met gebruik van twee spanningsmeters.#
# Jouw antwoorden
15.2.6. Methode#
In figuur 15.7 is de basisschakeling schematisch getekend. De range voor spanning over de diode waarbij de stroomsterkte gemeten moet worden is van 0.1 tot 0.6 V. In dit gebied verandert de stroomsterkte zeer sterk doordat de weerstand van de diode ongeveer 5 decades (\(10^5\)) groter wordt. Bij lage spanningen is de diodeweerstand zeer groot (M\(\Omega\)) en bij spanningen rond de 0.6 V over de diode is de diodeweerstand klein (h\(\Omega\)). De keuze voor de grootte van de Ohmse weerstand hangt sterk af van de weerstandswaarde van de diode. Hoe moeten we de waarde van de Ohmse weerstand R\(_1\) dan kiezen zodat de spanning over de diode goed te bepalen valt?
Kiezen we een hele grote weerstandswaarde, dan zal de spanningsmeter een merkbare invloed hebben op de gehele schakeling. Kiezen we een hele kleine weerstandswaarde, dan zal bij zeer lage spanning over de diode, vrijwel alle spanning over de diode staan. De precieze spanning over de weerstand is dan slecht te bepalen. De Ohmse weerstand moet dus een grote weerstandswaarde hebben, maar toch veel kleiner dan de interne weerstand van de DMM. De keuze voor de juiste weerstand is aan jou. Wel kun je met bovenstaande informatie na gaan wat een goede waarde is als je je bedenkt dat geldt: \(U_D=\frac{R_D}{R_D+R_1}U_{\text{bron}}\).
Omdat de weerstandswaarde van de diode zo sterk verschilt, is het lastig om een meetplan op te stellen op basis van een vast interval voor de spanningsbron (bijvoorbeeld van \(U_{\text{bron}}\) = 6.00 V tot 0.00 V in stappen van 0.25V). Om een gelijke verdeling van metingen over het interessegebied te krijgen, is het verstandig om iteratief te werken. Dat wil zeggen, voer een meting uit, zet de meting in een script, laat uitrekenen wat de spanning over de diode is, zet de meting in een plot, bepaal op basis daarvan wat de volgende meting moet zijn. Zo’n aanpak voorkomt een sterke clustering van punten rond \(U_D\) = 0.6 V wat de kwaliteit van een fit negatief beïnvloedt.
Een tweede probleem is de stabiliteit van de voeding bij lagere spanningen. De spanning is dan niet stabiel, en de onzekerheid in de spanning groot. Je kunt dit oplossen door gebruik te maken van een tweede spanningsdeler, zie 15.8 figuur. Doordat de spanning zich deelt over twee weerstanden is de spanning over de diodeschakeling ook kleiner.
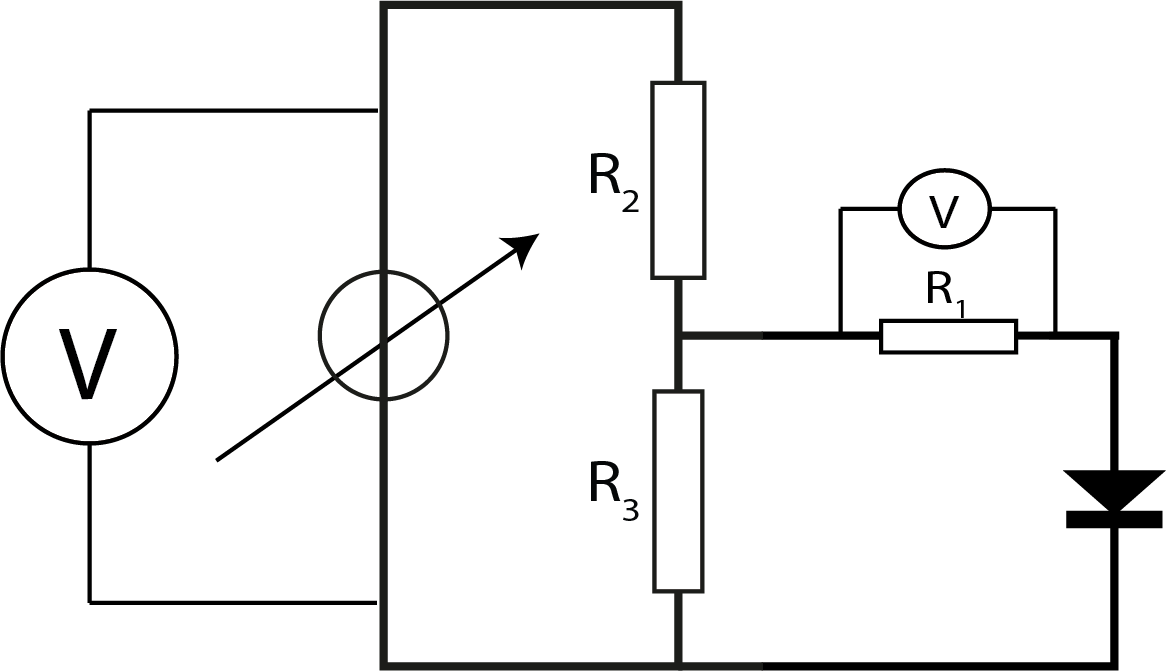
Fig. 15.8 De meetopstelling bestaat uit de diode en Ohmse weerstand in serie geschakeld met gebruik van twee spanningsmeters.#
Exercise 15.5
Bekijk figuur 15.8.
Laat zien dat de spanning over de diodeschakeling gegeven wordt door: \(U = \frac{R_3}{R_2+R_3}\cdot U_{bron}\).
Leg uit dat dit alleen geldt als \(R_3 << R_1 + R_D\)
Leg uit dat er een extra stap nodig is voor het berekenen van de spanning over de diode.
# Jouw antwoorden
Exercise 15.6
Schrijf het python script dat je in staat stelt om bovenstaande iteratieve proces uit te voeren. Maak gebruik van verschillende cellen: Ruwe data/bewerkte data/plot/fit.
Zet in het script je berekening voor de onzekerheid in \(U_{bron}\), \(U_R\) en \(R\) klaar. Deze kan je bij het uitvoeren van het experiment bepalen met behulp van de handleidingen.
Maak het script voor het vinden van de optimale fit, gebruik daarvoor vergelijking (15.1).
Maak het script voor het berekenen van de constante van Boltzmann op basis van de optimale fit parameters.
Uit de I-V karakteristiek van een diode kan een grootheid \(b\) bepaald worden. Volgens de theorie geldt: \(b=-q/nk_BT\) of \(k_B=-q/bnT\). \(q\) is de lading van een elektron (negatief), \(n\) de idealiteitsfactor en \(T\) de absolute temperatuur. Als we \(b\), \(q\), \(n\) en \(T\) kennen, kunnen we \(k_B\) bepalen. De onzekerheden in \(b\), \(n\) en \(T\) zijn \(u(b)\), \(u(n)\) en \(u(T)\). Leid een uitdrukking af voor de onzekerheid \(u(k_{\text{B}})\) in de gevonden waarde van \(k_B\).
# Jouw antwoorden
15.3. Uitvoering (3h)#
15.3.1. Weerstandsmetingen#
Op het perspexpaneel, zie Figuur 15.14, zijn verschillende weerstanden gemonteerd. Noteer de weerstandswaarden in een tabel. Houd ruimte voor twee extra kolommen in de tabel.
Meet met behulp van de \(3\frac{1}{2}\) digit DMM de weerstanden zo nauwkeurig mogelijk. Noteer de waarden in de tabel.
Meet vervolgens met de \(5\frac{1}{2}\) digit DMM de weerstandwaarden zo nauwkeurig mogelijk. Noteer ook deze waarden in de tabel.
Vind je dat de waarden gevonden met de \(3\frac{1}{2}\) digit DMM en \(5\frac{1}{2}\) digit DMM met elkaar overeenstemmen? Waarom? Bereken voor de kleinste weerstand, met behulp van de specificaties van de meters, de nauwkeurigheid van beide metingen. Zijn de waarden strijdig met elkaar? Laat zien.
Verdubbel de lengte van de meetsnoeren en meet de waarde de weerstandswaarde opnieuw. Wat heb je hiervan geleerd?
# Jouw antwoorden
15.3.2. Spanningsdeler#
Bouw met de weerstanden op het perspexpaneel schakeling zoals aangegeven in figuur 15.9. Tip: doe dit systematisch aan de hand van het schema. Ben je het overzicht kwijt? Breek alles af en begin opnieuw.
Stel de voedingsbron in op ongeveer 20 V. Meet nu de spanning met de \(5\frac{1}{2}\) digit meter direct over de voedingsbron (\(U_{\text{B}}\)), over \(R_{1}\) (\(V_{\text{AB}}\)) en over \(R_{\text{2}}\) (\(V_{\text{BC}}\)). Is \(U_B = V_{\text{AB}} + V_{\text{BC}}\) ?
Bepaal de verhouding van de spanning over \(R_{2}\) (\(V_{\text{BC}}\)) en de spanning over beide weerstanden \(R_{1}\) en \(R_{2}\) (\(V_{\text{AC}}\)). Laat zien dat dit klopt met wat we op grond van de gemeten waarden van de weerstanden (al gedaan bij opdracht 4-1) zouden verwachten.
Bereken de stroom die door de spanningsdeler loopt.
We gaan nu direct de stroom door de spanningsdeler meten met de \(3\frac{1}{2}\) digit DMM. Verander de instelling van de voedingsbron niet (controleer dit met de \(5\frac{1}{2}\) digit DMM). Plaats de stroommeter in het circuit zoals in figuur 15.10 is aangegeven. Meet de stroom. Klopt de gemeten waarde met de berekende waarde?
Verlaag de voedingsspanning met een factor 10. Verander verder niets. Welke stroom lees je op het 40 mA bereik van de \(3\frac{1}{2}\) digit DMM af? Schakel over het 4 mA bereik van deze DMM. Waarom wijkt de nu gevonden waarde af van de waarde op het 40 mA bereik? Wat moet je weten om het verschil kwantitatief te verklaren?
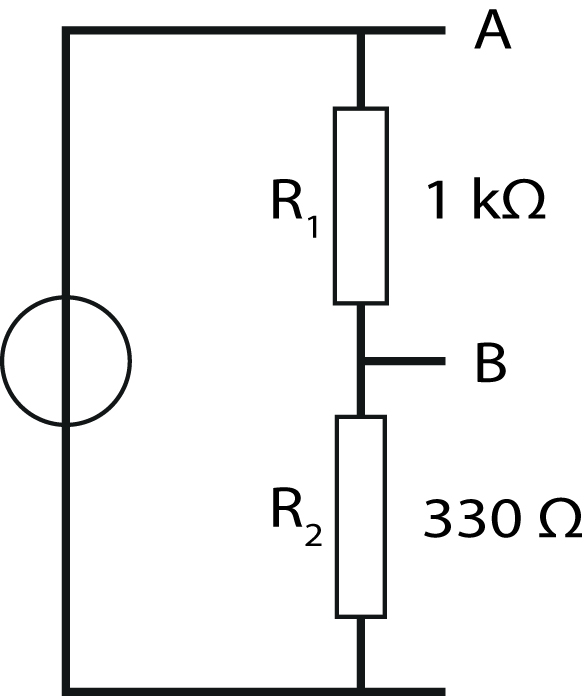
Fig. 15.9 De opstelling voor het meten van de spanningsdeling.#
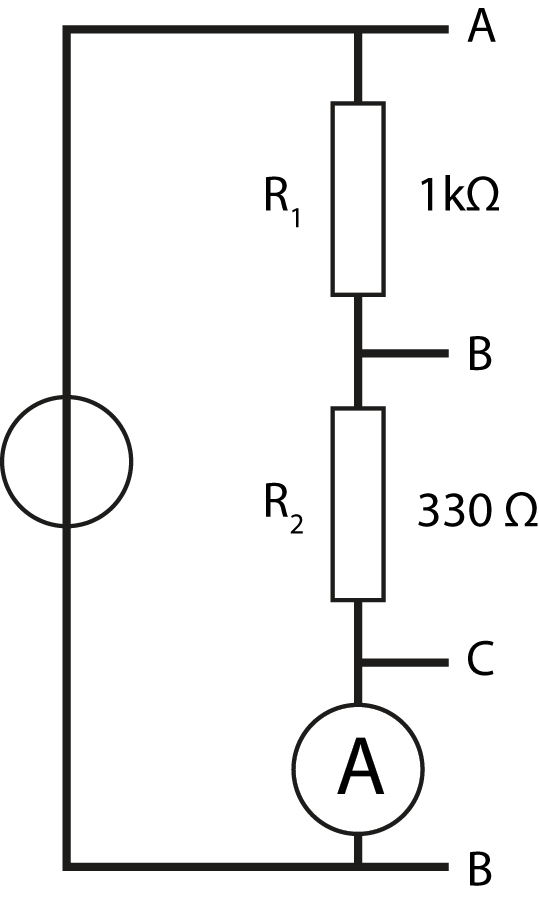
Fig. 15.10 De opstelling voor het meten van de stroomsterkte.#
# Jouw antwoorden
15.3.3. Diodemeting#
Bouw de opstelling zoals weergegeven in figuur 15.8. Gebruik de 3.5 DMM voor de spanning van de spanningsbron te meten, en de 5.5 voor de meting aan de weerstand die in serie staat met de diode.
Maak een foto van de opstelling en voeg deze toe aan je labjournaal.
Voer het iteratieve stappenplan uit.
Bereken op basis van de functiefit de constante van Boltzmann en de bijbehorende onzekerheid.
Laat je grafiek en bijbehorende gevonden waarde controleren.
Ruim de spullen zorgvuldig op.
# Jouw antwoorden
15.4. Achtergrond#
15.4.1. Elektrische schakelingen#
Veelal kunnen we een schakeling vereenvoudigen door een serie (of parallel) schakeling van twee weerstanden te vervangen door één weerstand. Als geheugensteuntje geven we hier een samenvatting van de formules die daarbij horen. Voor wie het niet meer precies weet: zie hfdst. 25-2 van Wolfson.
Fig. 15.11 Serie en parallelschakeling van twee weerstanden. Spanningsdeling en stroomdeling.#
Serieschakeling
Parallelschakeling
Gedissipeerd vermogen
15.4.2. Halfgeleiderdiode#
Bovenstaande Veritasium clip legt op een zeer gedegen manier de werking van een diode (hier dan een LED) uit. Alhoewel het gehele filmpje de moeite waard is, begint de uitleg over de werking rond 4:00.
Om de werking van een halfgeleiderdiode goed te begrijpen is een behoorlijke kennis van het gedrag van elektronen in halfgeleiders nodig. Dit onderwerp komt pas in het tweede of derde studiejaar aan de orde en dan is het nog niet zo eenvoudig. Voor de uitvoering van de proef is het niet noodzakelijk de werking van een diode te kennen. Omdat het voor velen onbevredigend is met iets te werken waarvan je niet weet hoe het werkt, laten wij hier eerst zien, hoe we met niet zo heel veel voorkennis, kunnen inzien waarom een halfgeleiderdiode in de ene stroomrichting wel en in de andere stroomrichting niet geleidt. We volgen hierbij de aanpak beschreven in hfdst. 24.2 p.403/404, 28.6 p.501 en 37.3 p.673-677 van Wolfson. Wie niet in de werking is geïnteresseerd, kan direct doorgaan naar sectie 5-4-2 waar de I-V-karakteristiek van de halfgeleiderdiode aan de orde komt, het onderwerp van dit deel van de proef.
Werking
Uiterst zuiver halfgeleider materiaal heeft bij lage temperatuur (b.v. kamertemperatuur of lager voor Si) zeer weinig vrije ladingsdragers en is daardoor een zeer slechte stroomgeleider.
De geleiding kan sterk worden verhoogd door het toevoegen van vreemde atomen. Dit wordt dotering of doping genoemd.
Voegen we aan Si een 5-waardig element toe, b.v. P, As of Sb, dan heeft dit element sterk de neiging één elektron los te laten. Dit elektron gedraagt zich als een vrij elektron en het zijn deze elektronen die ervoor zorgen dat in dit “n-type” materiaal, wel stroomgeleiding kan plaatsvinden.
Voegen we aan Si een 3-waardig element toe, b.v. B, dan heeft dit element sterk de neiging een elektron van een Si atoom te binden. Door dit proces ontstaat er een “gat” in de elektronen omringing van het Si atoom. Dit gat kan weer opgevuld worden door een elektron van een ander Si atoom, enz. Op deze manier beweegt het gat als het ware vrij door het materiaal. Het gat gedraagt zich als een positieve ladingsdrager. Het zijn de gaten die ervoor zorgen dat stroomgeleiding in dit “p-type” materiaal kan plaatsvinden.
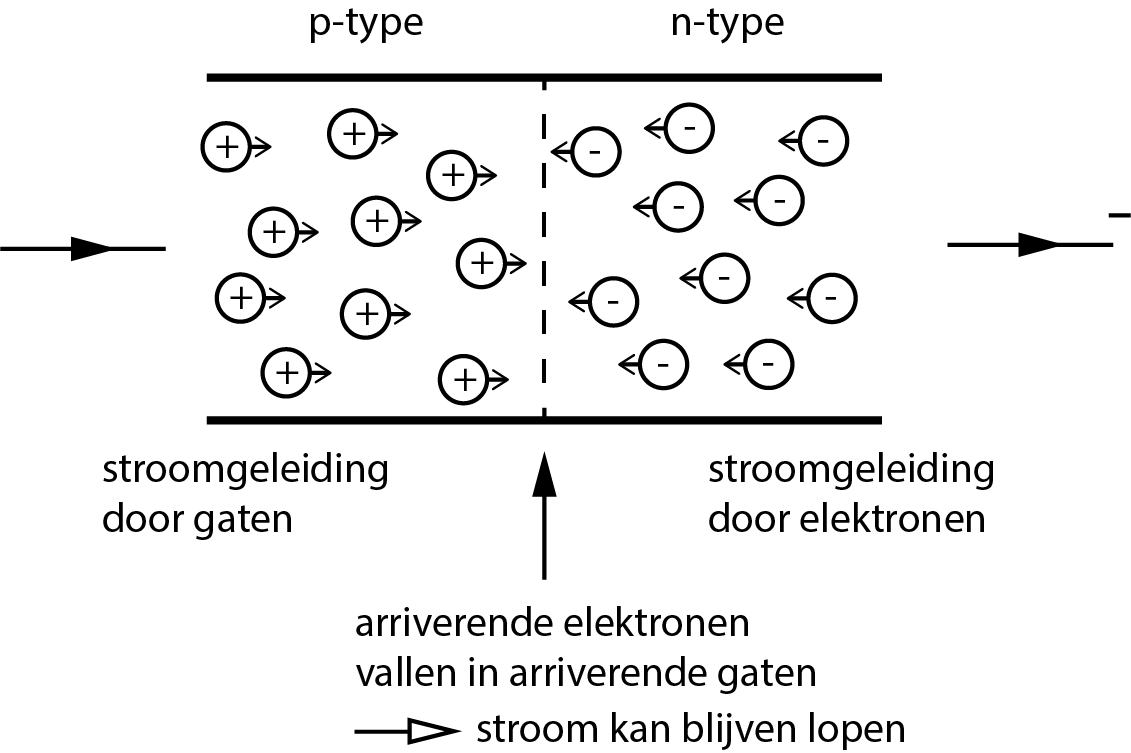
Fig. 15.12 Stroom door een halfgeleiderdiode. De pluspool van een spanningsbron is aangesloten op het p-type materiaal en de minpool op het n-type materiaal. Door recombinatie van gaten en elektronen nabij het grensvlak kan de stroom blijven lopen.#
Daar gebeurt iets bijzonders: de arriverende elektronen vallen in de arriverende gaten. Dit wordt recombinatie genoemd. Hierdoor raken we twee vrije ladingsdragers kwijt. Echter, door de aanwezigheid van de spanningsbron worden steeds nieuwe gaten en elektronen aangevoerd. Door dit proces ontstaat er een constante gaten (en elektronen) stroom naar het grensvlak. Van buiten af gezien denk je dat er gewoon een stroom van de plus naar de minpool loopt. Wij zeggen dat de diode in voorwaartse richting is geschakeld. Nu sluiten we de minpool van de spanningsbron aan op het p-type en de pluspool aan op het n-type materiaal.
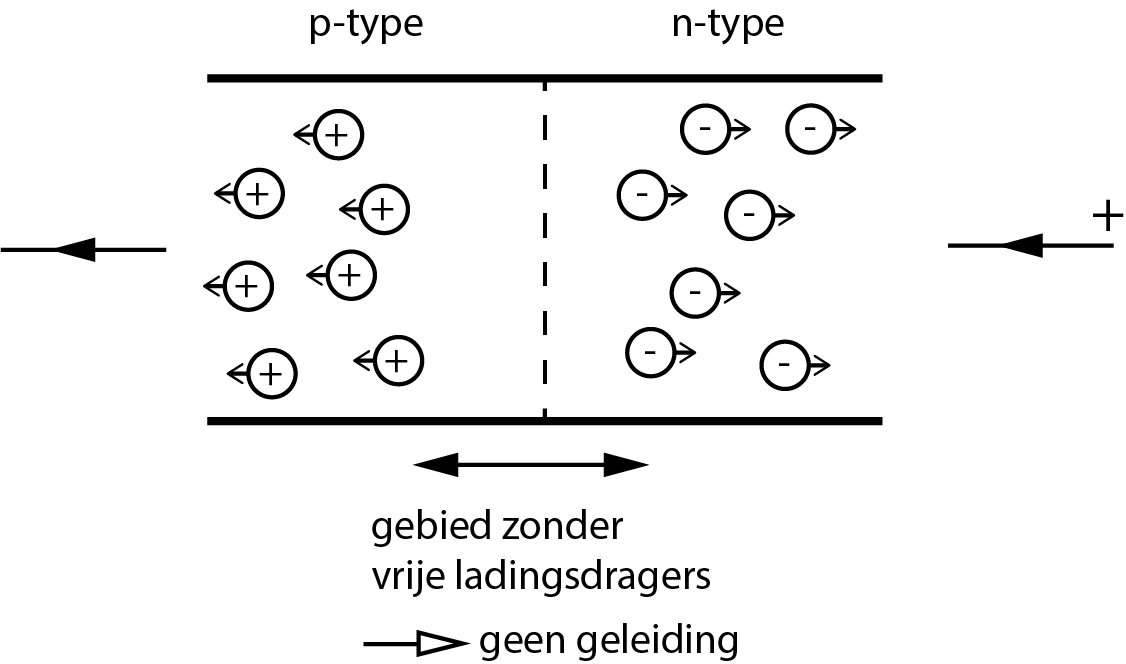
Fig. 15.13 De minpool van een spanningsbron is aangesloten op het p-type materiaal en de pluspool is op het n-type materiaal. Er kan nu geen stroom lopen omdat er een gebied zonder vrije ladingsdragers wordt gevormd.#
Dit is niet het hele verhaal. Zoals we weten hebben de elektronen (en gaten) niet allemaal dezelfde energie. In een halfgeleider is de energie van de elektronen (gaten) verdeeld volgens de Boltzmann verdeling. De gemiddelde energie van een elektron (gat) is \(k_{\text{B}} T\) (\(T\) is de absolute temperatuur en \(k_B\) is de Boltzmann constante). Het hangt nu van de hoogte van de barrière ten opzichte van \(k_{\text{B}} T\) af hoeveel elektronen (gaten) er over de barrière kunnen komen en dus hoeveel stroom er kan gaan lopen. De hoogte van de barrière wordt mede bepaald door de grootte van de voorwaartse spanning. Hoe hoger de voorwaartse spanning des te lager de barrière.
15.5. Materialen#
Fig. 15.14 Het elektronica boardje en de schematische weergave ervan.#