Labjournaal RC

13.7. Labjournaal RC#

13.7.1. Algemeen#

Namen:
Titel van het experiment: Inleiding gebruik oscilloscoop
Start datum:
Leerdoel: Werken met een functiegenerator en oscilloscoop
Practicumdoel: Bepalen van karakteristieken van een RC-circuit

#import necessary libraries
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit 
from IPython.lib.display import YouTubeVideo

13.7.2. Voorbereiding#

Lees het bijbehorende hoofdstuk en maak onderstaande vragen.

Opdracht 1

Op je oscilloscoopscherm zie je een periodiek pulsvormig signaal zoals hieronder.

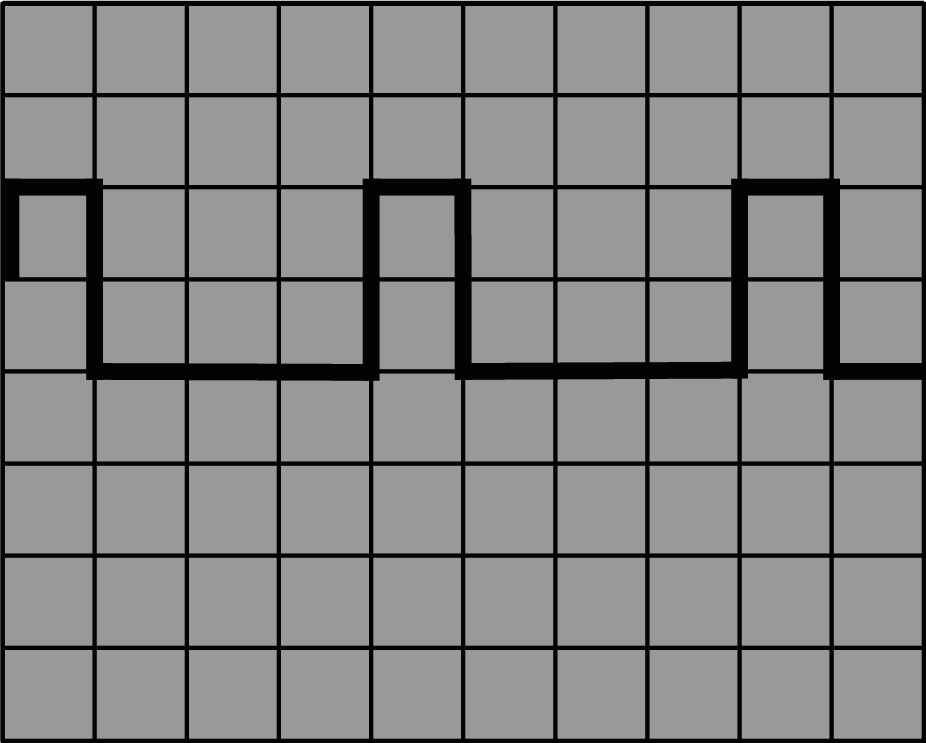
Bij de volgende instellingen:

  • Versterking: 2 V/div

  • Tijdbasis: 5 ms/div

  • Triggerhelling: +

  • Koppeling: DC

Bepaal de periode, de top-topwaarde en de pulsduur.

# ANTWOORD

Opdracht 2

  • Teken hoe het signaal weergegeven in onderstaande figuur zal worden wanneer het signaal links verder gaat waar het rechts eindigt.

  • De verticale gevoeligheid staat ingesteld op 0,2 V/div. Teken hoe het signaal op het beeld er uit zal zien als het triggerniveau wordt ingesteld op 0,35 V, zowel voor slope+ als slope-.

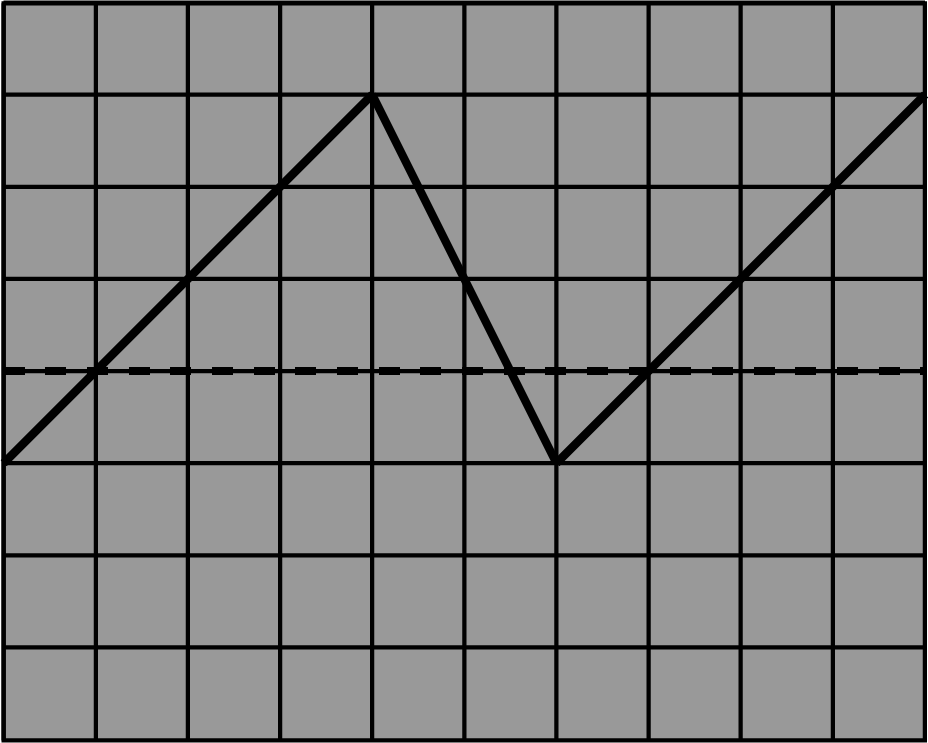
# ANTWOORD

Opdracht 3

Op je tweekanaalsoscilloscoop is onderstaand beeld zichtbaar van twee in fase verschoven sinusvormige signalen A en B. Daarbij is signaal A op ingang Y1 (of Ch 1) aangesloten en signaal B op ingang Y2 (of Ch 2).

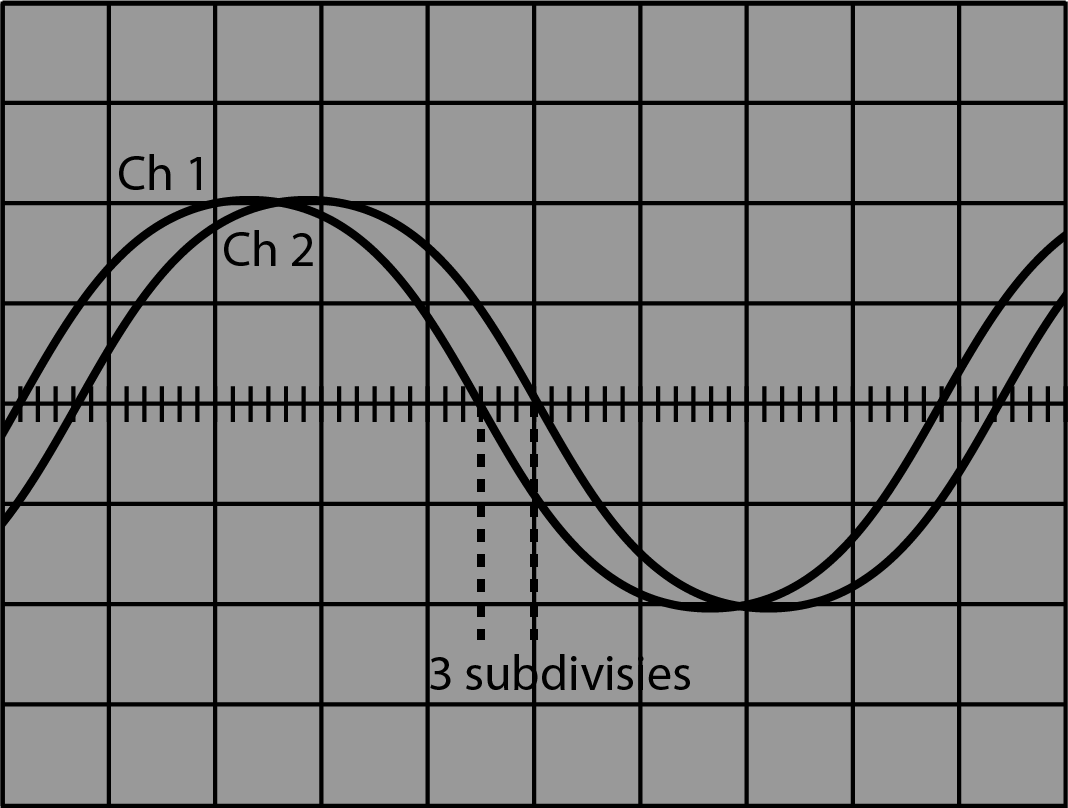
*Weergaven van twee periodieke signalen. Met de instellingen: Versterking: 1 V/div, Trigger: Kanaal Ch2.*

  • Geef aan welk signaal (Ch1 of Ch2) in fase vòòr loopt op het andere.

  • Bepaal het faseverschil in graden.

  • Wat is het ingestelde triggerniveau (in V)?

  • Wat is de ingestelde triggerhelling (+ of -)?

# ANTWOORD

Opdracht 4

Op je oscilloscoopscherm levert een periodiek pulsvormig signaal op. Als de ingangskoppeling (AC-GND-DC) op GND wordt gezet, is een vrijlopende horizontale lijn zichtbaar die samenvalt met de horizontale rasterlijn in het midden.

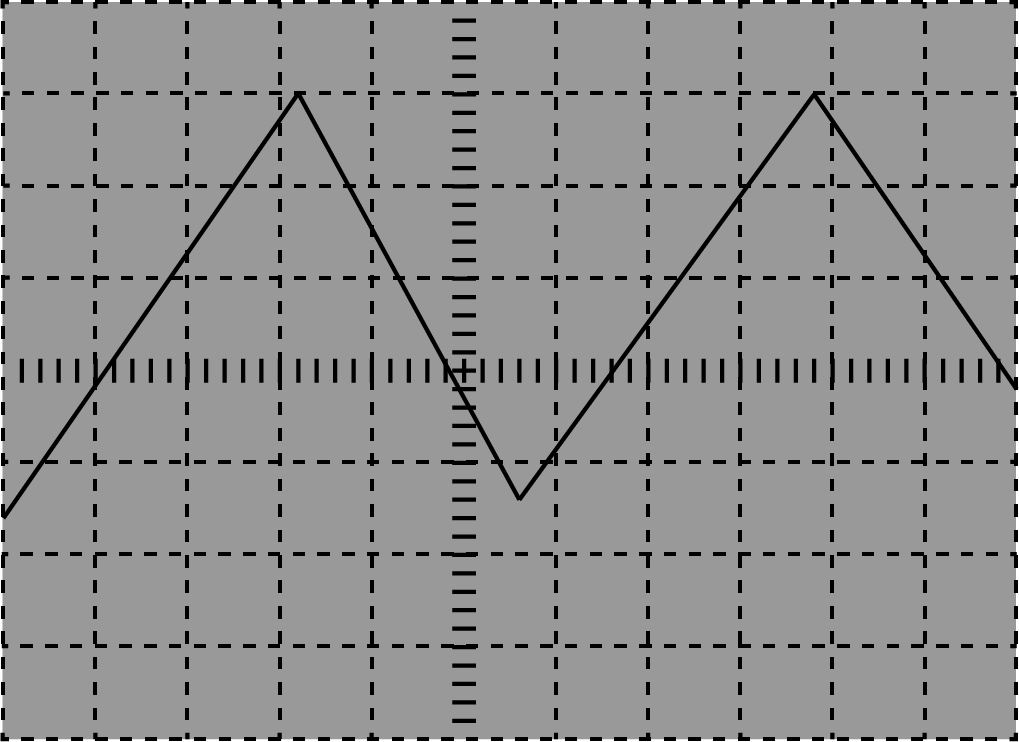
*Weergaven van een periodiek signaal. Met de instellingen: Versterking: 2 V/div, Tijdbasis: 5ms/div, Triggerhelling: +, Koppeling: DC*

  • Wat is het triggerniveau (in V)?

  • Wat is de periode van het signaal (in ms)?

  • Wat is de frequentie van het signaal (in Hz)?

  • Wat is de tijdsduur van de neergaande flank van het signaal?

  • Waaraan kun je zien daty de ingagskoppeling op DC staat?

#ANTWOORD

Opdracht 5

We bieden een 5.0 Hz, 5.0 Vpp wisselspanning aan voor een LED in serie met een 220Ω weerstand. De drempelspanning van de LED is 1.7 V.

  • Stel de vergelijking op voor de aangeboden (bron)spanning.

  • Bereken hoeveel procent van een periode de LED stroom door laat.

  • Teken een enkele cyclus van de aangeboden spanning als functie van de tijd.

  • Teken in dezelfde grafiek de spanning over de weerstand als functie van de tijd.

  • Leg uit hoe je aan de hand van dit signaal de drempelspanning van de LED kunt bepalen.

  • Leg uit wat er gebeurt met de felheid van branden en hoe het gemeten signaal verandert als je een off-set spanning toevoegt.

#ANTWOORD

13.7.3. LAB-opdrachten#

De uitwerkingen van de opdrachten, zoals gemeten en berekende getalwaarden, grafieken, argumenten, etc. moeten tijdens het experimenteren overzichtelijk in dit (digitale) laboratoriumjournaal worden genoteerd, zodat over deze proef, wanneer gewenst, een verslag kan worden geschreven. In deze proef zijn een aantal opdrachten opgenomen.

  1. Een introductie in begrijpen van AC-DC signaal.

  2. Een introductie van de basisfunctionaliteit van een digitale oscilloscoop (opdracht aan de hand van een RC-circuit).

  3. Cursorfunctionaliteit van een digitale oscilloscoop en het uitgebreider gebruik.

  4. Het gebruik van het RC circuit met een ruis signaal.

  5. Het bepalen van de karakteristiek van een LED.

13.7.3.1. 1. AC-DC-stand (∼ 10 min)#

In deze opdracht onderzoek je het effect van de verschillende standen.

  • Verbind de functiegenerator (OUTPUT) met de oscilloscoop (1) d.m.v. BNC kabel.

  • Zet de functiegenerator aan, druk op blokspanning.

  • Stel de frequentie in op 1.0 Hz en een Vpp van 2.0 V en druk op OUTPUT (deze gaat branden als die aanstaan, anders geeft die überhaupt geen signaal).

  • Zet de oscilloscoop aan en bekijk het beeld bij AC en DC stand.

  • Hoe ziet je verwachtte signaal er uit?

  • Met welke stand is dit overeenkomstig? Verklaar het andere signaal.

  • Wat zegt dit over de stand die je nodig hebt bij de andere experimenten?

  • Onderzoek het effect bij verschillende frequenties. Wat is je conclusie?

# ANTWOORDEN

13.7.4. 2. Introductie digitale oscilloscoop: de faseverschuiving in een RC-circuit. (∼75 min)#

Het doel van dit experiment is om de eerste stappen in het meten met een oscilloscoop te zetten. Je zult zien dat je vrij vlot uitgebreide analyses kunt doen met de verschillende functies van de oscilloscoop en dat het daarom een veelgebruikt meetinstrument is. In het eerste experiment doe je metingen aan een RC-circuit, waarbij je onderzoek doet naar de theorie zoals beschreven in de theoretische achtergrond.

Voor dit experiment heb je de signaalgenerator, de oscilloscoop, elektronica board nr 1 met condensatoren en weerstanden en een aantal kabels nodig. De schematische weergave van de testopstelling is hieronder weergegeven.

Gebruik de 33 nF condensator en de 4.7 kΩ weerstand en sluit de signaalgenerator aan als bron. Voer de volgende stappen uit:

  • Sluit een (T-) splitter aan op de OUTPUT van de signaalgenerator.

  • Verbind een BNC-banaan kabel (connector aan de signaalgeneratorkant) met de splitter.

  • Verbind de andere zijde van de BNC kabel met het testboard ({numref}`Figuur {number} ), de rode kabel van de BNC met de linkerkant 4.7 kΩ weerstand, de zwarte kabel met de van de 33 nF.

  • Verbind de 33 nF door met de 4.7 kΩ weerstand.

Nu heb je een gesloten circuit met een 4.7 kΩ en een 33 nF.

  • Verbind de nog open uiteinde van de splitter van de functiegenerator met een BNC-BNC kabel aan kanaal 1 van de oscilloscoop. Kanaal 1 meet het oorspronkelijk signaal.

  • Dan rest nog het aansluiten van de oscilloscoop. Dat doen we met de BNC-verloopstekker te zien op Figuur 13.8. Aan de stekker is niet te zien wat de plus en wat de minus kant is. Als het signaal niet lijkt te kloppen, draai de stekker om.

  • Kanaal 2 van de oscilloscoop moet de spanning over de condensator meten. Sluit de BNC naar BNC kabel aan op kanaal 2 en op het testboard zodat je de spanning over de condensator meet. Bedenk zelf hoe dit moet!

Stel de volgende zaken in op de signaalgenerator, zonder de spanning aan te zetten: frequentie op 100 Hz, sinusgolf, DC offset uit of op 0 en amplitude op 1.0 V. Kies voor utility -> Output setup -> High Z ipv een load. Sommige signaalgenerators hebben een multiplier voor de frequentie, houd hier dus rekening mee bij het instellen. Zet tot slot de signaalgenerator aan en druk op AUTO of AUTOSCALE (oscilloscoop). In 90% van de gevallen levert dit een prima beeld op.

Als het goed is staan er nu twee signalen op het scherm van de oscilloscoop, het signaal direct uit de signaalgenerator op kanaal 1 en de spanning over de condensator op kanaal 2. Probeer de volgende zaken uit en kijk of je een gevoel kunt krijgen voor manipuleren van signalen:

  • Bekijk de tijdbasis en de gevoeligheid van de signalen onderin het scherm, kloppen deze met wat je op basis van je inputsignaal verwacht?

  • Manipuleer met de knoppen onder het kopje HORIZONTAL de tijdbasis en -offset.

  • Manipuleer met de knoppen onder het kopje VERTICAL (of kanaal 1 / kanaal 2) de verticale gevoeligheid en -offset van beide signalen. Zorg dat beide signalen overlappen nadat je klaar bent.

  • Druk op de oplichtende knop van kanaal 1 en schakel dit kanaal in DC modus, als dat nog niet zo was. Herhaal voor kanaal 2. Dit verschil is bij deze frequentie overigens als het goed is vrij klein (maar wel waarneembaar!).

  • Trigger het signaal. Druk daartoe op mode/coupling of Trig menu. Kies voor slope omhoog. Draai aan de triggerknop en kijk wat er gebeurt. Druk nu op slope omlaag, wat gebeurt er met het signaal dat je ziet? Zet de slope weer op omhoog.

  • Probeer in het Measure-menu (meestal een knop met dito naam) een aantal interessante grootheden op het scherm te plotten, denk aan peak-to-peak voltage van kanaal 2, frequentie en het faseverschil. Wat kun je zeggen over de nauwkeurigheid van deze drie grootheden? Waar heeft dat mee te maken? Noteer.

  • Speel nu met de frequentie op de signaalgenerator. Beide signalen veranderen duidelijk op het scherm. Stel de signaalgenerator in op ongeveer 5000 Hz en stel de oscilloscoop handmatig bij totdat het signaal weer duidelijk zichtbaar is op het scherm. Als het goed is overlappen beide signalen nu niet meer, maar is er een duidelijk faseverschuiving en is de amplitude van de spanning over de condensator kleiner geworden. Verantwoord voor jezelf dat dit strookt met de gegeven theorie.

#ANTWOORDEN

Gebruik de formules beschreven in de theoretische achtergrond en verifieer dat de faseverschuiving en de gain overeenkomt met wat je meet. Voer daartoe de volgende opdrachten uit:

  • Draai de signaalgenerator terug naar ongeveer 1 Hz en pas de tijdbasis aan totdat er enkele periodes van het signaal op het scherm passen. Dit duurt even, omdat de oscilloscoop meerdere secondes nodig heeft om dit signaal te ‘sparen’.

  • Open een Excelsheet of text editor en maak drie kolommen; frequentie, faseverchuiving en Vpp. Gebruik als je een text editor gebruikt een ; of , als scheidingsteken tussen alle waardes in een rij.

  • Vul deze tabel met ongeveer 4 rijen per decade, meet door tot ongeveer 100 kHz. (Dus: 1 Hz, 2 Hz, 4 Hz, 8 Hz voor de eerste decade, 10 Hz, 20 Hz, 40 Hz, 80 Hz voor de tweede, etc.) Je hoeft niet exacte deze frequenties te meten, zolang je maar nauwkeurig opschrijft welke frequentie je wel hebt gemeten. Pas de tijdschaal en verticale gevoeligheid van kanaal 2 aan zodat beide signalen goed zichtbaar blijven en de meting nauwkeurig blijft. Noteer ook observaties m.b.t. de kwaliteit van het signaal en de metingen. Sla het bestand op als csv. LET OP! Meet de Vpp van kanaal 2, de spanning over de condensator dus! (LET OP! Krijg je bij lage frequenties een faseverschuiving, dan staat je input nog op AC ipv DC).

  • Laad je databestand in in je Jupyter Notebook en plot de faseverschuiving tegen de frequentie (frequentie op de x-as). Plot in dezelfde grafiek de theoretische faseverschuiving op basis van de formules uit de theoretische achtergrond. Zet de x-as op de log-schaal. Bepaal ook op basis van een curvefit voor zowel de faseverschuiving als voor de spanningsoverdracht de RC waarde. Zijn deze gelijk aan elkaar?

  • Houd je opstelling zoals die is, bij de volgende opdracht maak je er weer gebruik van.

#ANTWOORDEN & PLOTS & FIT

13.7.4.1. RC-circuit vervolg: RC-tijd en het low-pass filter. (∼ 45 min.)#

Een condensator bestaat dus uit twee platen waar je lading op kunt slaan. Als er een gelijkspanning over de condensator gezet wordt, zal deze langzaam ‘vollopen’. Bij de start van het opladen zal de spanning met name over de weerstand staan, maar deze spanning verschuift langzaam naar de condensator.

Een karakteristieke tijd voor het vollopen is de RC-tijd \(τ = RC\). De RC-tijd is gelijk aan de tijd die nodig is om de spanning over de condensator gelijk aan 63,2% (\(1 − e^{−1}\)) van de bronspanning te laten zijn en volgt op logischer wijze uit de formule voor de spanning over de condensator: $\(V(t) = V_0 \cdot e^{-\frac{t}{RC}}\)$

Bij een wisselspanning zal de condensator opladen en vervolgens weer ontladen. Als de frequentie van de wisselspanning heel hoog is, zal de condensator zich gedragen als een draad zonder weerstand. De stroomsterkte wordt dan met name bepaald door de weerstandswaarde en de spanning over de condensator zal klein zijn. Dat de spanning over de condensator sterk afneemt is goed te zien vanaf een bepaalde frequentie, de cutoff frequency: $\(f_{cutoff} = \frac{1}{2πRC}\)$ Beide eigenschappen van een RC-circuit onderzoeken we in dit deel van het practicum.

Bepaling van de RC-tijd

  • Reken de cutoff frequentie uit voor het RC-circuit dat nog aangesloten is van het vorige onderdeel.

  • Stel de frequentiegenerator in op een blokspanning met een frequentie van \(\frac{1}{2}f_{cutoff}\).

  • Stel met behulp van de time knop van de oscilloscoop (horizontal) de tijdbasis zo in dat je circa vijf blokspanningen ziet. Bereken daartoe eerst op welke tijdschaal (sec/div) de oscilloscoop grofweg moet staan.

  • Trigger het signaal op het kanaal met de minste ruis.

  • Maak een foto van je signaal en voeg deze hieronder toe.

# ANTWOORDEN

De RC-tijd bepalen kan op verschillende manieren. We voeren de bepaling eerst handmatig uit om bekend te raken met de verschillende functies achter de knoppen van de oscilloscoop. Daarna gebruiken we automatische opties van de oscilloscoop.

  • Stel de tijdschaal zo in dat je een enkele blokgolf of een deel van de blokgolf op je scherm ziet. Druk op single, dit levert een enkel, vast beeld op, een opname. Je kunt vervolgens in en uitzoomen op bepaalde delen van het beeld. Zorg dat de RC-karakteristiek goed in beeld is en maak hier weer een foto van en voeg deze hieronder toe.

  • De spanning bereikt 63,2% van het spanningsverschil na de RC-tijd. Tel het aantal hokjes totdat deze 63,2% bereikt is: dit geeft een eerste grove schatting.

# ANTWOORDEN

Om de RC-tijd nauwkeuriger te bepalen, bepalen we nu eerst de minimale en maximale spanning. Vervolgens bepalen we de waarde zodat \(U_C = 63, 2\%ΔU\).

  • Druk achtereenvolgens op: Measure / Voltage / Vpp; Vmax; Vmin Onder in je beeld staan nu de verschillende waarden: Vpp de top-topwaarde, Vmax de maximale spanning, Vmin de minimale spanning.

  • Bereken met behulp van deze waarde de spanning waarbij geldt: \(U_C = 63,2\%ΔU\). We willen de waarde voor t nauwkeurig aflezen bij de juiste spanning. Dit kan met behulp van tracking met de cursor functie.

  • Druk op cursor en vervolgens op Track. Nu verschijnt er een tracking punt op je signaal die je omhoog en omlaag kunt bewegen met de draaiknop rechtsboven op de oscilloscoop. Wanneer je drukt op curB komt er een tweede tracking punt. Zoek de verschillende waardes voor de spanning en de bijbehorende tijd op waarmee je \(τ\) kunt bepalen. \(Δx\) in het scherm komt overeen met \(τ\). Vergelijk je gevonden waarde met de eerder berekende en bepaalde RC-tijd.

# ANTWOORDEN

Er is een tweede manier om snel de RC-tijd te bepalen. Dit kan m.b.v. de rise time. Dit is de tijd die nodig is om het signaal van 10% naar 90% van de maximale spanning te krijgen. De rise time is gelijk aan 2.2\(τ\).

  • Druk op Measure / Time / Rise time. Zoom in op het stuk waar de grafiek omhooggaat.

  • Noteer alle gevonden waarden hieronder overzichtelijk in een tabel. Welke manier van de RC-tijd bepalen vind je het best? Waarom?

# ANTWOORDEN

13.7.4.2. 4. Het low-pass filter (∼ 20 min.)#

Bij het vorige onderdeel heb je al informatie verzameld over het low-pass filter. Draai nog een keer door de verschillende frequentieschalen heen om het gedrag van het RC-circuit in het perspectief van de nieuwe informatie uit deze opgave te plaatsen. Wat gebeurt er met de spanning over de condensator boven en onder de cutoff frequency?

  • Laad de dataset van het eerdere onderdeel in met en plot de Vpp van kanaal 2 tegen de frequentie op de log-logschaal (plt.xscale(‘log’), etc).

  • Bepaal m.b.v. de grafiek de cutoff frequency en vergelijk deze met de theoretische waarde.

13.7.4.3. Low-pass filter toegepast#

Een Low-Pass Filter kan heel handig zijn om ruis uit een signaal te filteren. Om te kijken hoe goed dit werkt, gaan we een signaal met ruis aanbieden aan het circuit. Hiervoor gebruiken we hetzelfde circuit als in de vorige opdracht en de mogelijkheid om de computer met de functiegenerator te verbinden. Gebruik hiervoor de desktop op je bureau het dichtst bij de caddy: deze is namelijk via USB aangesloten op je functiegenerator.

  • Download en open het bestand met de golf: sineWaveWithNoise.xls (staat op Brightspace). Let op, dit bestand bevat macro’s, dus het is essentieel om inhoud in te schakelen als Excel dat in een banner vraagt.

  • Bovenin de excel file kun je de amplitude (VPP) en frequentie invullen. Indien gewenst kan eventueel de ruisfrequentie ook aangepast worden. In de grafiek staan zowel de golf die we willen vinden als het ruissignaal weergegeven.

  • Druk op de functiegenerator op de knop Utility, vervolgens op I/O en vervolgens op Show USB Id. Neem de code die hier staat over in cel D3 van je excel bestand.

  • Test of alles werkt door een voltage van 2 VPP en een frequentie van 1 Hz in te stellen en de knop ‘Send to Function Generator’ in te drukken.

Het signaal dat naar de functiegenerator wordt gestuurd is opgebouwd uit een sinus golf met de bovenaan ingevoerde frequentie, en een ruis met een 100 maal zo hoge frequentie, resulterend in de blauwe golf weergegeven in de grafiek in je excelbestand, die als het goed is overeenkomt met het signaal op kanaal 1 van de oscilloscoop.

  • Bij welke frequentie(s) verwacht je dat het filter optimaal zal werken, zodanig dat je een zo hoog mogelijke signaal-ruis ratio (S/N) hebt? Wat verwacht je te zien bij een lagere of hogere frequentie?

  • Stel de frequentie in op de cutoff frequency uit de vorige vraag, en bekijk kanaal 2 van de oscilloscoop.

Voeg een foto of tekening van dit signaal toe aan je labjournaal.

  • Bekijk nu wat er gebeurt bij andere frequenties tot 3 decades van de cutoff frequency. Noteer voor elke decade (dus 6 in totaal) of het filter slechter, beter of even goed werkt. Voldoet dit aan je verwachtingen?

  • Indien uit de resultaten van de vorige vraag geen duidelijk verschil te zien is in de kwaliteit van het filter, ben je waarschijnlijk bij de verkeerde frequentie begonnen. Doorloop je berekening nogmaals en kijk of je de juiste frequenties kunt vinden.

#ANTWOORDEN

13.7.4.4. 5. Meten aan een LED (∼ 20 min.)#

In deze opdracht kijken we naar het karakteristieke gedrag van een LED. Bouw de volgende opstelling:

  • Verbind de 330 Ohm weerstand in serie met de LED.

  • Maak de schakeling gesloten door de functiegenerator aan te sluiten op de weerstand en LED.

  • Meet de spanning over de weerstand met de oscilloscoop. Aan de BNC banaan stekker is niet te zien wat de plus en wat de minus kant is. Als de spanning over de weerstand niet lijkt te kloppen, draai de stekker om.

  • Sluit de drie BNC kabels aan. Gebruik bij de functiegenerator een T splitter waarbij het afgegeven signaal zowel naar de oscilloscoop gaat (channel 2) als naar het testboard. Doe de volgende opdrachten:

  • Bied een 5.0 Hz, 5 \(V_{pp}\) ingangssignaal aan en vergelijk het beeld dat de oscilloscoop toont met het signaal dat je in een van de voorbereidingsopdrachten hebt getekend.

  • Verklaar de overeenkomsten en verschillen tussen het door jouw getekende signaal en het gemeten signaal.

  • Bepaal met behulp van de oscilloscoop de drempelspanning van de LED. Wat verwacht je dat er met de felheid van branden gebeurt als je gebruik maakt van een positieve offset spanning? Wat verwacht je dat er met het gemeten signaal gebeurt als je gebruik maakt van een positieve offset spanning? Controleer je voorspellingen en verklaar de verschillen, als die er zijn.

#ANTWOORDEN

Ruim nu netjes op en laat je caddy controleren. Maak vervolgens je labjournaal af en laat het aftekenen door de TA.

Contents