15. Proef van Millikan#
Note
Dit is een oud experiment waarvan de documentatie ontbrak. Ontbreekt er informatie of is er informatie onjuist, dan horen we dat graag!
De proef van een Millikan is een klassiek natuurkunde experiment. Het idee is dat je kleine oliedruppeltjes kunt laten zweven tussen twee condensatorplaten. Omdat de lading gekwantificeerd is en de massa en het aangebrachte elektrische veld bepaald kunnen worden, kun je de elektrische ladingskwantum bepalen.
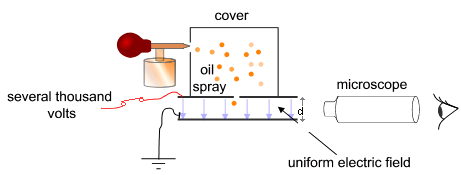
Fig. 15.1 Schematische opstelling van de proef van Millikan, figuur via Wikimedia Commons (commons)#
15.1. Theorie#
Voor deze proef zijn er twee mogelijke uitvoeringen, de eerste is met zwevende druppeltjes, de tweede met druppeltjes die bewegen met een constante snelheid.
15.1.1. Zwevende druppeltjes#
Voor zwevende druppeltjes geldt dat de zwaartekracht werkende op de druppeltjes gelijk is aan de elektrische kracht die werkt doordat de druppeltjes geladen zijn:
Hierin is \(\rho_d\) de dichtheid van de druppel, \(\rho_l\) de dichtheid van lucht, \(V\) de volume van een druppel, \(U\) de spanning tussen de platen die een onderlinge afstand \(d\) hebben, \(n\) het aantal elektronen en \(e\) de elementaire ladingskwantum. Let op! Een extra hulp hier is dat \(n\) een geheel getal is.
15.1.2. Constante snelheid#
Wanneer de druppeltjes bewegen met constante snelheid is er wrijvingskracht in het spel. De grootte van deze kracht wordt gegeven door de wet van Stokes:
Hierin is \(\eta\) de viscositeit van lucht, \(r\) de straal van de druppel en \(v\) de snelheid van de druppel. Deze vergelijking geldt alleen onder bepaalde voorwaarden. Omdat de druppels klein zijn (\(0.5*10^{-6}\))m is deze in de orde van de vrije weglengte van gasmoleculen (\(0.07*10^{-6}\)m) en moet er een correctiefactor in rekening gebracht worden. Dit zorgt ervoor dat de no-slip conditie niet geldt aan de rand van de druppels. De viscositeit moet hierdoor gedeeld worden door een correctiefactor van \(k=1+\frac{b}{p\cdot r}\) waarin de correctiefactor \(b=80 \textrm{μm} \cdot \textrm{hPa}\), \(p\) de druk in Pa en \(r\) de straal van de druppel (in m).
Voor de straal van de oliedruppel geldt:
hierin is \(v_g\) de valsnelheid zonder extern E-veld.
Exercise 15.1
Laat zien dat bovenstaande vergelijking voor de straal van de oliedruppel geldt.
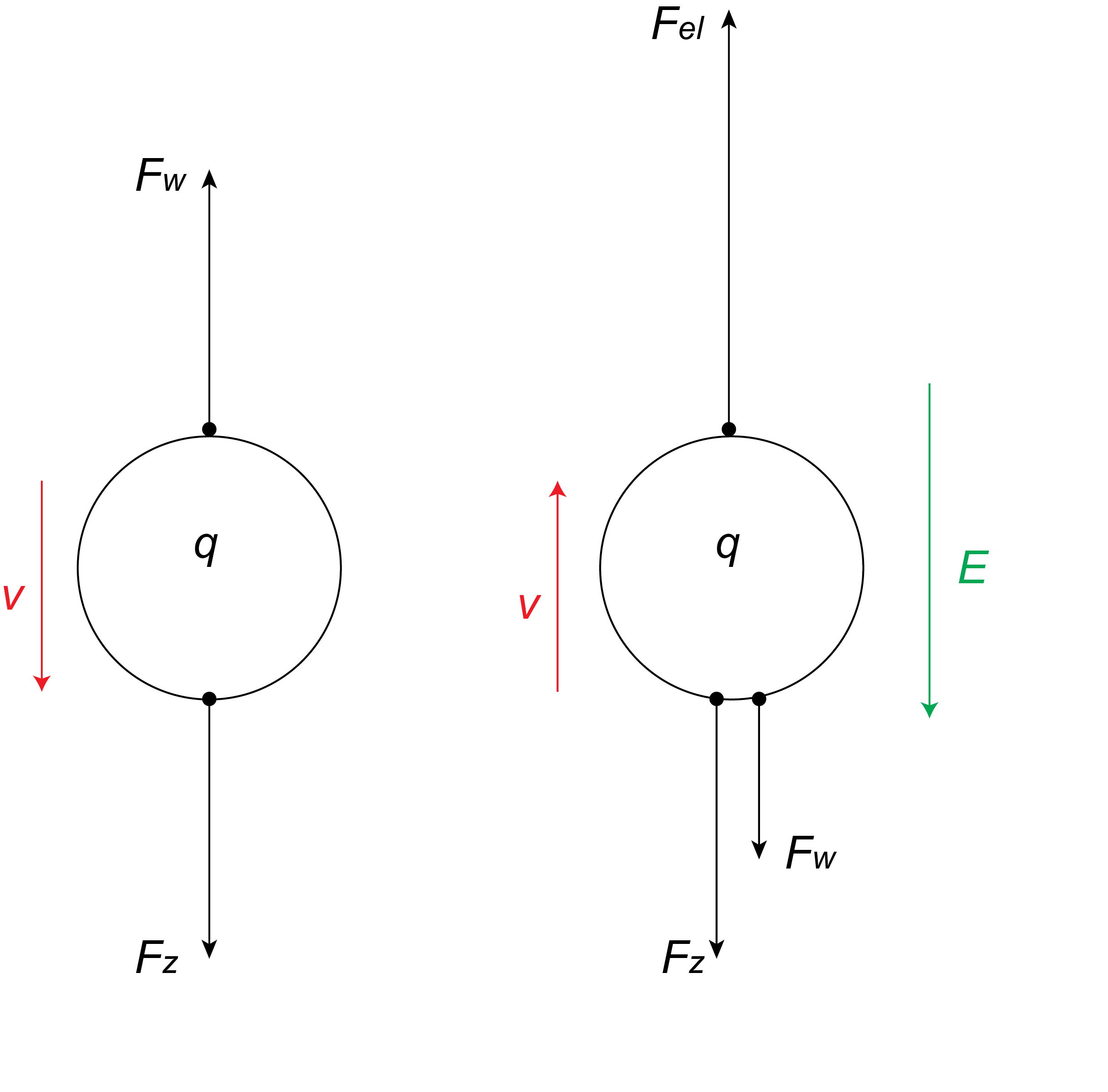
Fig. 15.2 De krachten die werken op een geladen oliedruppel die beweegt met een constante snelheid.#
Een handigheid die we kunnen toepassen is het elektrische veld omdraaien. Door de krachtenbalans voor een meewerkend elektrisch veld en een tegenwerkend elektrisch veld (tegen de zwaartekracht in) van elkaar af te trekken, vervalt de zwaartekrachtsterm.
Exercise 15.2
Voer bovenstaande exercitie uit en geef de vergelijking die je krijgt voor de elektrische lading.
15.2. Apparatuur#
De aanwezige apparatuur omvat:
a. Een millikan cel met verlichtingsmogelijkheden.
b. Een regelbare gelijkspanningsbron.
c. Een voltmeter.
d. Een microscoop met een oculairglaasje met ijkschaaltje.
e. Een ijkschaaltje.
f. Een olieverstuiver.
g. Een telefoon houder of webcam
15.3. Uitvoering#
In deze proef worden de tijden gemeten die een geladen oliedruppeltje nodig heeft om een bepaalde afstand in lucht af te leggen, zowel met als zonder elektrisch veld. De olie wordt verneveld in de condensator door in de olieverstuiver te knijpen. Deze druppels kunnen dan gevolgd worden met het oculair. De te bepalen afstand komt overeen met de afstand tussen twee vooraf gekozen streepjes op het ijkschaaltje in het oculair.
Om de proef nauwkeurig uit te voeren, is het belangrijk om druppeltjes te selecteren met verschillende groottes en met ladingen (\(q\)) kleiner dan ongeveer 10 keer de elementaire lading. Dit houdt in dat je de metingen moet richten op druppeltjes waarvan de looptijden binnen specifieke intervallen vallen. Aangezien de exacte waarde van de elementaire lading (\(e\)) nog niet bekend is, kunnen deze intervallen niet direct worden berekend. In theorie zou eerst een ruwe experimentele schatting van \(e\) nodig zijn om deze intervallen te bepalen. Omdat hiervoor niet genoeg tijd is, wordt bij de voorbereiding van de proef aangenomen dat \(e = 2 \cdot 10^{-19}\mathrm{~C}\).
Daarnaast zijn de volgende gegevens van het Millikan-apparaat nodig:
Afstand tussen de platen van de Millikan-cel: \((6,36 \pm 0,02) \cdot 10^{-3}\) m.
Afstand tussen de streepjes op het ijkschaaltje: \((\approx 1/20) \cdot 10^{-3}\) m.
Dichtheid van de olie: zie metingen
Viscositeit van lucht bij kamertemperatuur: \(1,8 \cdot 10^{-5}\) kg/m·s.
Spanningsverschil tussen de platen: instelbaar van 0 tot 600 V.
Exercise 15.3
Kloppen al deze waardes? ga dit na.
15.4. Voorbereiding#
Bereken als onderdeel van de voorbereiding in welke intervallen de looptijden ongeveer moeten liggen opdat de lading van het druppeltje kleiner is dan ongeveer 10 elektronladingen.
Bepaal voor een aantal druppeltjes de looptijden en bereken hieruit hun ladingen \(q\). Pas, indien nodig, de correctie op de wet van Stokes toe. De constante die daarbij een rol speelt heeft een waarde van ongeveer \(8.2\cdot10^1\) Nm\(^{-1}\).
Bereken \(e\) uit de gevonden ladingen. Doe dit bijvoorbeeld grafisch. Bedenk hierbij dat \(q = ne\) met \(n\) geheeltallig, zodat \(q\) uitgezet tegen \(n\) een rechte lijn moet opleveren door de oorsprong. Om deze rechte te vinden zet men verticaal de gevonden \(q\)-waarden uit en horizontaal \(n\). Alle punten (\(n\),\(q\)) in het vlak zijn mogelijke punten van deze rechte. Trek door de oorsprong een rechte zodat zo goed mogelijk is voldaan aan \(q = ne\). Uit de richtingscoëfficiënt van deze lijn volgt \(e\).
Exercise 15.4
Is dit altijd juist? Leg uit.
15.5. Metingen aan dichtheid#
### Siliconenolie
V_so = np.array([0, 1.9, 1.7, 1.55, 1.40, 1.10, 1.0, .75, .55, .4, .25]) #mL
m_so = np.array([3.48, 5.56, 5.36, 5.20, 5.00, 4.73, 4.54, 4.36, 4.12, 3.94, 3.80 ]) - 3.48 #g
# Petroleumolie
V_po = np.array([4.4, 4.5, 5.3, 6.8, 7.2, 9.3, 9.4, 11.6, 13.9, 14.6, 16.9, 18.9]) #mL
m_po = np.array([3.40, 3.56, 3.95, 5.30, 5.57, 7.15, 7.36, 9.06, 10.89, 11.57, 13.38, 14.9 ]) #g
