Labjournaal

11. Labjournaal#

11.1. General#

Template for labjournaal. See https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Working With Markdown Cells.html for options to use markdown.

#import necessary libraries
import matplotlib.pyplot as plt
import numpy as np
import math
from scipy.optimize import curve_fit

Names:

Title of the experiment: Validation of the relation between force and distance of two magnets.

Starting date:
Expected enddate:

Goal of the experiment: In this experiment we determine the relation of the force between two magnets as function of their mutual distance. We use the set up shown below:

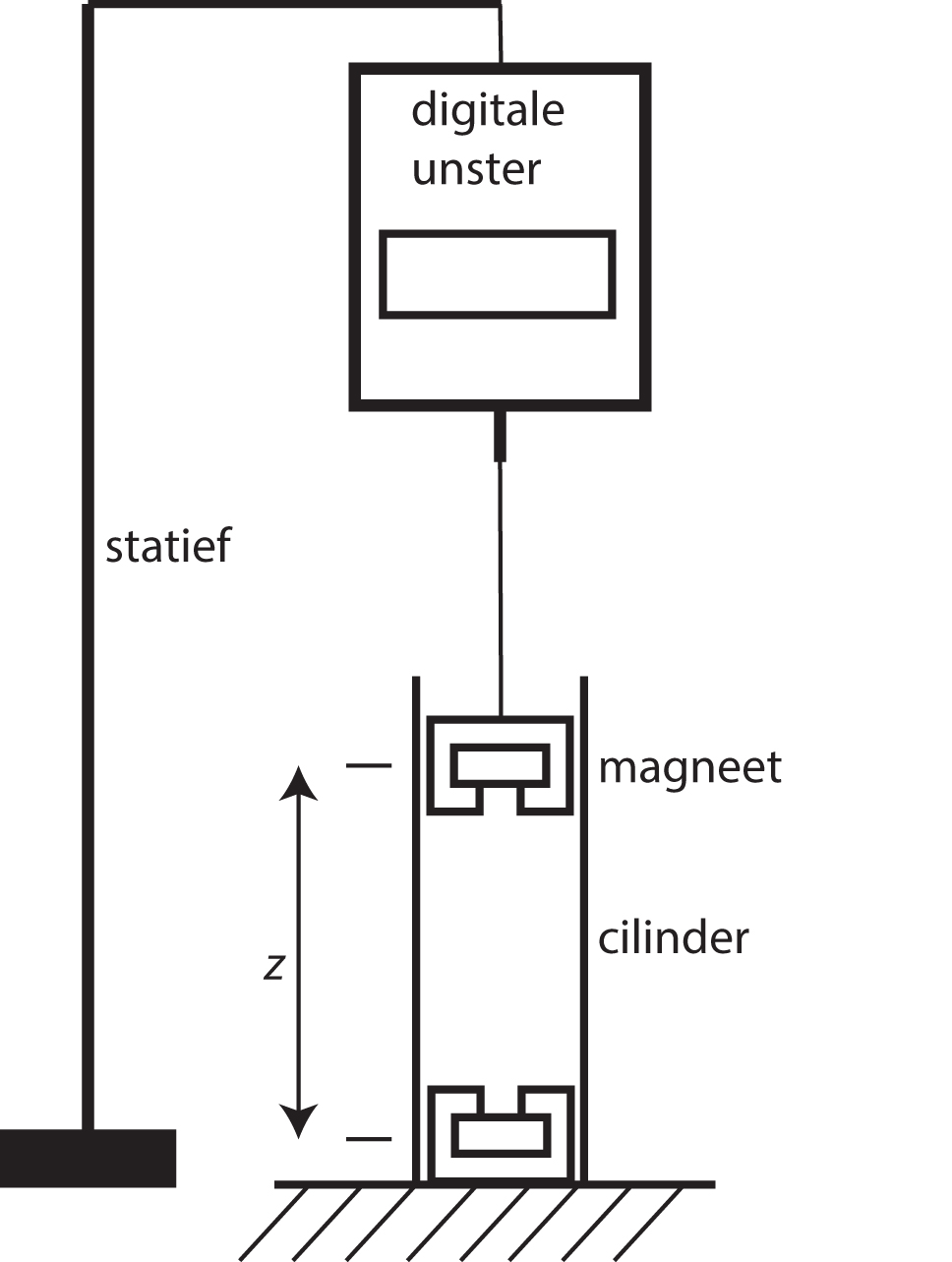
../_images/opstelling.jpg

The heart to heart distance between the two magnets can be calculated:

../_images/ie1_opst_onz.png

Research question:

Expectations or Hypothesis:

Desired accuracy:

11.2. Preparation#

Assignments:

Method:

Theory:

Independent variable:
Dependent variable:
Controlled variablen:

Measurement instruments & Settings:

#Metingen vooraf
d_m = 
u_d_m = 

h_1_aan = 
u_h_1_aan =

h_1_af = 
u_h_1_aF =

h_2 = 
u_h_2 =

Procedure:
Setup(drawing or picture):

Notes:
About accuracy:

11.3. Execution#

# Measurements: Explain the names of variables provide only raw data in np.arrays!
#Raw measurements
h_12_af = np.array([   ,   ,  ,\
                       ,   ,  ,\
                       ,   ,  ,\
                       ,   ,  ,\])

F_af =    np.array([   ,   ,  ,\
                       ,   ,  ,\
                       ,   ,  ,\
                       ,   ,  ,\])*9.81

h_12_aan = np.array([   ,   ,  ,\
                        ,   ,  ,\
                        ,   ,  ,\
                        ,   ,  ,\])

F_aan =    np.array([   ,   ,  ,\
                        ,   ,  ,\
                        ,   ,  ,\
                        ,   ,  ,\])*9.81

Observations:
Notes:

11.4. Processing#

Description of processing of raw data into scientific evidence:

z_aan =

z_af =

11.4.1. Data processing and analysis:#

First look at your data without considering measurements uncertainty. Use the next cell to insert your code to plot your measurements. Consider the rules producing graphs!

#Data processing and analysis:
#(F,z)-plot 
plt.figure()
**[your code]**
plt.show()

Based on the plot, are you allowed to combined the two datasets into one? If so, merge the arrays.

#merge arrays 
z = 
F =

Now plot the same measurements with errorbars. You can use this source to find out additional options: https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.errorbar.html

#Data processing and analysis:
#(F,z)-plot with errorbars
plt.figure()
**[your code]**
plt.show()

11.5. Fitting the data#

11.5.1. function fit using \(z^{-4}\)#

There are at least two options to use a function fit to your measurements. We will look at the different methods to analyse your data below.

As we expect the function to be in the form: \( F = \frac{a}{z^4} \) we can ask Python to fit this function. You can use this source to find out additional options: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html Think about whether measurements with the outcome \(F\) = 0 N count or should be disregarded.

def func(x,a):
	return a/x**4

popt,pcov = curve_fit(func,z,F)
pcov
print('alpha = ', popt[0], '+/-', np.sqrt(pcov[0,0]))

The printed value is the constant in the function \( F = \frac{a}{z^4} \). Make a new plot in which you show your measurements and your function fit. Part of the code is already written for you.

#(F,z)-plot with errorbars and functionfit
plt.figure()


**[your code]**

min_value_z = 
max_value_z =

x = np.linspace(min_value_z,max_value_z,1000)
y = func(x,*popt)

plt.plot(x,y,'r--',linewidth=1)   
plt.show()

11.5.1.1. Residual analysis#

It is always interesting to see whether the fit is a good fit. The fit above might not be the easiest way to directly see this. We therefor use a residual analysis. In this analysis we plot our measurements - our fit. The code gives some idea of what to do. Analyse the residuals by completing the code below.

# Residual analysis
plt.figure()
plt.plot(z,func(z,popt[0])-F,'k.',linewidth=1)   
plt.show()

11.5.1.2. fitting with systematic error#

You were able to measure the heart-to-heart distance with a certain accuracy. You probable had to use some kind of reference point. Using a reference might lead to a systematic error. A systematic error can be introduced by looking at the function \(F=\frac{a}{(z+\Delta z)^4}\), where \(\Delta z\) is our systematic error. Investigate whether there is a systematic error in your data.

11.5.2. linear fit#

Another option is a linear fit. As we expect the function to be in the form: \( F = \frac{a}{z^4} \) we can replace \( z^{-4} \) by \( u \). Our function will then be a linear function: \( F = a \cdot u \). This is known as coordinate transformation and is already taught at secondary school level (so you should have some experience with it!).

Make a new variable \( u \) with the values of \( z^{-4} \) and plot the graph. Make it an interactive plot (%matplotlib notebook) where you can zoom in on certain parts of the graph. Does it look linear to you?

#(F,u)-plot without errorbars 
plt.figure()
u =
**[your code]**
plt.show()

The errorbars are still missing in the plot. As \( u = z^{-4} \), \( u_u = 4 \cdot u_z \cdot z^{-5} \).

Proof this.

Calculate the uncertainties for \( u \) and errorbarplot (\( F \), \( u \)).

#(F,z)-plot with errorbars 
plt.figure()
**[your code]**
plt.show()

Carry out the following steps:

  • define the function for the functionfit

  • curve fit

  • plot your measurements and the curve fit

  • make it an interactive plot so that you can zoom in and see all essential features of the graph

#(F,z)-plot with errorbars and functionfit
plt.figure()
**[your code]**
plt.show()

Make additional plots that are relevant for the experiment in the given context.

#additional plots of interest
plt.figure()
**[your code]**
plt.show()

There is at least one additional way to see what kind of exponential function (\( y = a*x^n \)) is used. One can use a log-log-plot to see whether n = -4 and constant! Explore this way of analyzing the data.

#extra analysis
plt.figure()
**[your code]**
plt.show()

Maybe you are not satisfied with the result… find out whether there is a different relation than \( F = \frac{a}{z^4} \) that better matches your experimental data, e.g. \(F = a \cdot z^{n}\)…

11.6. Calculating the remanent field#

If your data concords with the formula: \(F=\frac{\alpha}{z^4}\), we still have to see whether the remanent field is similar to the value specified by the manufacturer. This analysis consists of the following steps:

  • produce the value of \(\alpha\) and its associated uncertainty

  • using this value, calculate the remanent field \(B_r\)

  • calculate the associated uncertainty

  • produce an agreement analysis (strijdigheidsanalyse) to see whether the values are in agreement.

Execute this analysis.

Describing the pattern in the processed data:

#Calculations of e.a. measurement uncertainties, and providing final answers.

Notes:

11.7. Discussion#

11.8. Conclusion#

11.9. Additional notes, remarks, explanations, thoughts etc#

Contents