14. Val met wrijving#
Waarom valt een baksteen sneller dan een veer? Elk object dat zich beweegt door een medium ondervindt een wrijvingskracht. Op de middelbare school mocht je deze kracht waarschijnlijk meestal verwaarlozen, maar in veel alledaagse situaties is dit niet realistisch. Een regendruppel zou dan bijvoorbeeld met een snelheid van enkele duizenden meters per seconde op je hoofd vallen…
Op basis van de onderstaande theorie kun je een experiment bedenken waarbij je bijvoorbeeld de wrijvingscoëfficient van een vallende waterdruppel - of een ander object - bepaalt. Ook kun je kijken naar de wrijving van een object in een vloeistof, of iets anders dat te maken heeft met de omstroming van lichamen.
14.1. Wrijving bij beweging door een medium#
De onderstaande sectie is gebaseerd op het tweede hoofdstuk van Transport Phenomena: The Art of Balancing by Harry van den Akker & Robert F. Mudde (Delft: Delft Academic Press, 2014), 109-120.
14.1.1. Drag force#
Elk object dat door een vloeistof of gas heen beweegt ondervindt een wrijvingskracht. Deze kracht wordt ook wel de drag force genoemd, aangeduid met \(F_D\). De drag force is afhankelijk van de viscositeit \(\mu\) en de dichtheid \(\rho\) van de vloeistof of het gas, de relatieve snelheid \(v_r\) van het object ten opzichte van de (onverstoorde) vloeistof, en de typische afmeting \(D\) van het object. In het algemeen heeft deze de volgende vorm:
waarin \(\textrm{Re} = \frac{\rho v_r D}{\mu}\) het Reynoldsgetal is (Hierin is \(\rho\) de dichtheid van de vloeistof in kg/m\(^3\), \(v\) de snelheid in m/s, \(D\) de karakteristieke lengte schaal in m en \(μ\) de dynamische viscositeit in Pa·s.). De meest rechter factor \(\rho v_r^2\) is een mate voor de traagheid van de vloeistof of het gas. Zoals we zouden verwachten verzet een vloeistof of gas dat ‘zwaarder’ is, of sneller stroomt, zich harder tegen de beweging van het object. De tweede factor, \(D^2\), heeft de dimensie van een oppervlakte. Ook dit is niet verrassend: de kracht werkt op de oppervlakte van het object. De meest linker term \(f(\textrm{Re})\) houdt rekening met de specifieke vorm en stroming rond het object. Het Reynoldsgetal Re kan worden gezien als een indicator van het stromingsregime rond een object: bij een lage Re is de stroming laminair (in laagjes), en bij een hoge Re turbulent (chaotisch). Het stromingsregime maakt veel uit voor de krachten die werken op het object. Hoe de drag force precies afhankelijk is van Re, wordt onder andere bepaald door de specifieke vorm van het object.
Om de bewegingsvergelijking op te stellen, kun je je voorstellen dat je een lichte piepschuimen bal van een balkon laat vallen. Naast de zwaartekracht die werkt op het voorwerp is er een opwaartse kracht (wet van Archimedes) en is er een wrijvingskracht die tegengesteld is aan de bewegingsrichting van het voorwerp (meesleepkracht of ‘Drag Force’ in het Engels).
De resulterende kracht \(F_D\) kan worden opgedeeld in de bijdragen van twee afzonderlijke effecten: form drag en friction drag. Form drag ontstaat door de druk die wordt opgebouwd aan het oppervlak van het object doordat vloeistof of gas deeltjes hier tegenaan stromen. Een extreem voorbeeld is een vlakke plaat die recht op de stroomrichting wordt gezet: Aan de voorkant van de plaat ontstaat een hoge druk door de deeltjes die hier tegenop botsen. Aan de achterkant van de plaat ontstaan wervels, en is de druk veel lager. Dit drukverschil resulteert vervolgens in een kracht tegen de stroomrichting van de plaat in.
Friction drag is het resultaat van wrijving van de vloeistof of het gas met het oppervlak van het object waar het langs stroomt. Dit wordt het beste geïllustreerd door een vlakke plaat die parallel in de stroomrichting ligt. De plaat ondervindt wrijving op het oppervlak parallel aan de stroomrichting, vergelijkbaar met die van een skiër op een helling. De grootte van deze wrijvingskracht hangt af van de de ruwheid van het oppervlak. Zie ook Figuur 14.1.
In het algemeen is de wrijvingskracht op een object de optelsom van de krachten die resulteren van deze twee mechanismen, \(F_D = F_{form} + F_{friction}\). Beide krachten hebben de vorm van verg. (14.1).
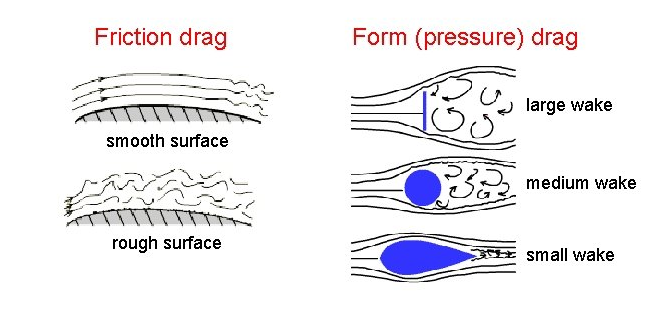
Fig. 14.1 Illustratie van de twee vormen van tegenwerkende kracht die een stromend object in een vloeistof of gas ondervindt. Afbeelding verkregen van deze site.#
Vaak wordt voor de totale drag force de volgende vergelijking gebruikt:
waarin wordt aangenomen dat de vloeistof of het gas het object met een uniforme snelheid nadert. \(A_{\perp}\) is hierin het oppervlakte loodrecht op de stroomrichting. \(C_D(\textrm{Re})\) is de drag coefficient die afhangt van de vorm en grootte van het object en de eigenschappen van de vloeistof of het gas, net zoals de functie \(f(\textrm{Re})\) in verg. (14.1). Alleen in uitzonderlijke gevallen kan de drag coefficient analytisch bepaald worden. De belangrijkste aannames bij Stokes flow zijn:
De stroming wordt gedomineerd door de visceuze krachten, Re « 1.
De terugstroming is zeer klein, oftewel de diameter van de bal is vele malen kleiner dan de diameter van de buis.
De vloeistof is onsamendrukbaar (\(\frac{d\rho}{dt} = 0\)) In dat geval geldt:
De typische afmeting \(D\) voor een bol is de diameter, of tweemaal de straal \(R\). Het geprojecteerde oppervlak van een bol loodrecht op de stroomrichting is \(A_{\perp} = \pi R^2\). De drag force wordt dan dus:
Deze vergelijking staat bekend als de wet van Stokes. Voor de bijdragen van de form drag en friction drag afzonderlijk geldt:
Voor veel objecten is de drag coefficient empirisch bepaald als een functie van Re. In Figuur 14.2 is de drag coefficient voor de stroming rond een bol, cilinder en schijf. Zoals te zien in de figuur geeft de wet van Stokes een goede benadering voor de drag coefficient voor de stroming rond een bol bij een lage Re, maar wijkt deze daarna sterk af.

Fig. 14.2 Wrijvingscoëfficient \(C_D\) voor een bol, cilinder en schijf als functie van het Reynoldsgetal Re. De stippellijn laat de wet van Stokes zien. Afbeelding verkregen van: Rony Caballero et al. *Six Degree of Freedom Underwater Vehicle for Culvert Inspection}, International Conference on Climbing and Walking Robots and the Support Technologies for Mobile Machines, Poznan, Poland, 21 – 23 July 2014#
Wanneer het Re-getal groter wordt, ontstaan er aan de achterzijde van het object wervels (zie Figuur 14.3). Er is dan een zog gevormd; de grenslaag heeft ``losgelaten’’ van het deeltje ten gevolge van de traagheid van het omhullende medium, dat het liefst rechtuit blijft gaan. (N.B.: Deze redenering gaat uit van een medium dat het deeltje omstroomt, maar die situatie blijkt gelijkwaardig te zijn aan de situatie waarbij het deeltje zich door het medium beweegt, als in de proef.) Bij grotere Re-getallen worden de wervels groter en schuift het punt waar de grenslaag loslaat meer naar voren. Bij nog grotere Re-getallen (\(10^3\) - \(2\times10^5\), Newton regime) wordt het zog onregelmatig en turbulent. Er worden dan wervels door de stroming meegenomen en nieuwe achter het deeltje geproduceerd. Uiteindelijk wordt bij zeer hoge Re-getallen de grenslaag turbulent en schuift het punt waar de grenslaag loslaat terug naar de achterzijde van het deeltje. In het overgangsgebied van Stokes naar Newton regime kunnen we gebruik maken van de Schiller-Naumann relatie:
Voor objecten die met hoge snelheid door een ijl medium bewegen (\(10^3<\text{Re}<2\times10^5\)) toont Figuur 14.2 dat \(C_D\) bij benadering constant is.
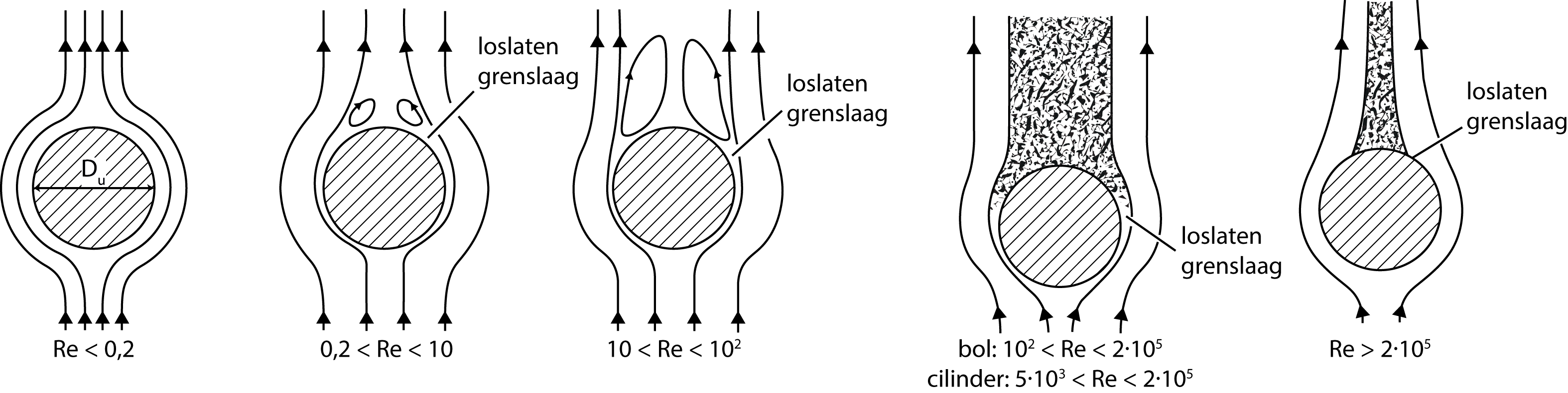
Fig. 14.3 Stromingspatroon rondom een bol als functie van het Re-getal.#
14.1.2. Terminale snelheid#
Wanneer een object vanuit stilstand in de lucht wordt losgelaten zal deze in eerste instantie versnellen. Naarmate de snelheid van het object toeneemt, zal ook de wrijvingskracht op het object toenemen (zie verg. (14.1)). Op een gegeven moment zullen de krachten in balans zijn, en blijft de snelheid van het object constant. De maximale snelheid die een vallend object bereikt wordt de terminale snelheid genoemd.
Stel we hebben een bolvormig object dat met een constante snelheid \(v_t\) valt door de lucht, zoals weergeven in Figuur 14.4. Op het object werken drie krachten: de zwaartekracht, een wrijvingskracht en een opwaartse kracht (ook wel de archimedeskracht of drijfkracht genoemd). Voor een bol met diameter \(D\) en dichtheid \(\rho_b\) is de zwaartekracht gelijk aan:
waarin \(g\) de zwaartekrachtversnelling is. De wrijvingskracht wordt gegeven door verg. (14.2), en is gelijk aan:
hierin is \(\rho_l\) de dichtheid van de lucht. De opwaartse kracht is gelijk aan het gewicht van de lucht in het volume dat door de bol wordt ingenomen. Deze is dus:
Wanneer de snelheid constant is, geldt volgens de tweede wet van Newton: \(\sum F = F_g + F_D + F_{opw} = 0\). Als we de uitdrukkingen voor de individuele krachten in deze vergelijking invullen, kunnen we deze herschrijven tot:
wat ons een uitdrukking geeft voor de terminale snelheid van het object. Er doet zich echter één probleem voor; de snelheid in verg. (14.4) is afhankelijk van de drag coefficient \(C_D\). Deze is echter op zijn beurt weer afhankelijk van het Reynoldsgetal Re \( = \frac{\rho_l v_t D}{\mu}\), en dus ook van de snelheid. Deze circulaire afhankelijkheid kan worden omzeild met en iteratief proces: Eerst wordt een schatting gedaan van Re, waarmee de terminale snelheid \(v_t\) wordt berekend. Vervolgens wordt de berekende snelheid gebruikt om Re te bepalen, die dan weer kan worden gebruikt om een nieuwe snelheid te berekenen. Dit proces wordt herhaald tot de snelheid niet meer veranderd.
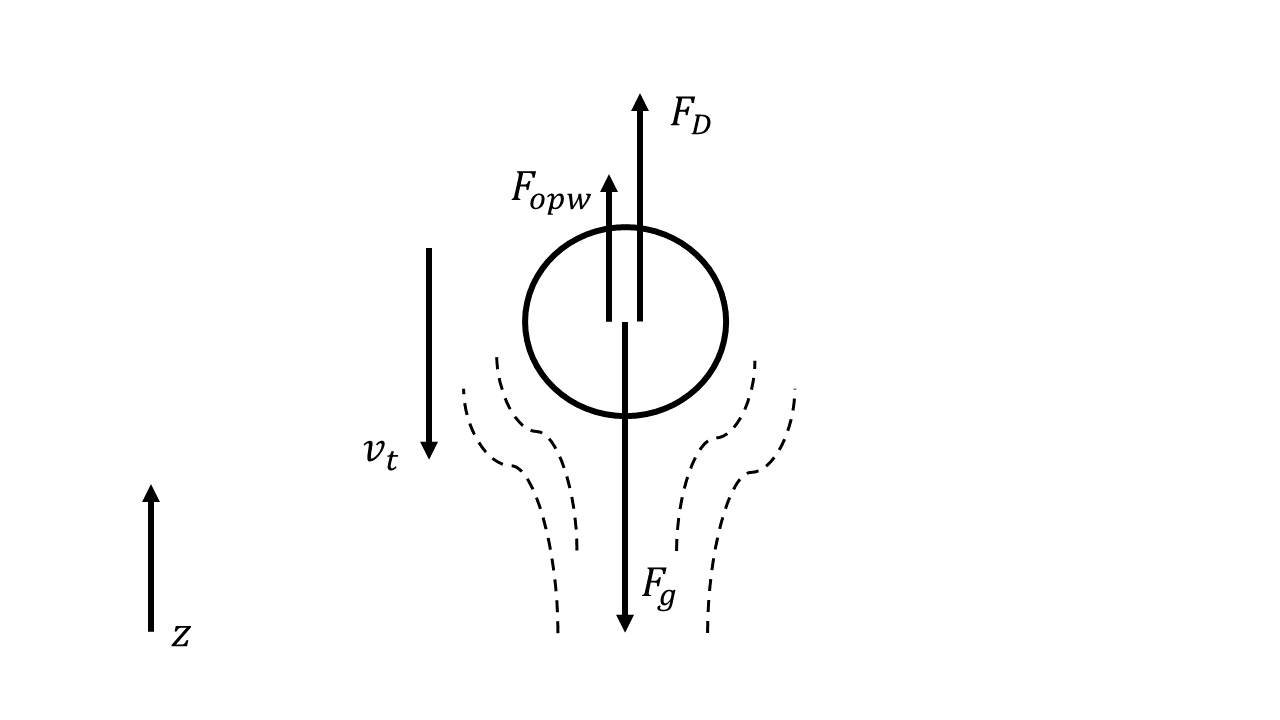
Fig. 14.4 Bolvormig object dat met een constante snelheid \(v_t\) valt door de lucht. Op de bol werken drie krachten: de zwaartekracht \(F_g\), een wrijvingskracht \(F_D\), en een opwaartse kracht \(F_{opw}\).#
Voorbeeld
Stel we hebben bolvormige hagelsteen (\(\rho_{ijs}=915\) kg/m\(^3\)) die valt door de lucht (\(\rho_{l} = 1.205\) kg/m\(^3\), \(\mu_l = 1.82\cdot10^{-5}\) Pa s). De diameter van de hagelsteen is \(D = 1.00\) cm. We schatten het Reynolds getal op Re \(= 10^2\). In Figuur 14.2 kunnen we dan aflezen dat \(C_d\) ongeveer 1 bedraagt. Dit invullen in verg. (14.4) geeft een terminale snelheid van \(v_t = 9.96\) m/s. Als we deze snelheid vervolgens weer gebruiken om Re te bepalen krijgen we Re = \(6.59\cdot10^3\). Dit geeft een \(C_D\) van ongeveer 0.4. De snelheid die hieruit volgt is \(v_t = 15.7\) m/s, wat weer leidt tot Re \(=1.04 \cdot 10^4\). Deze Re waarde geeft weer een \(C_D\) van 0.4, en de snelheid verandert niet meer. De terminale snelheid van de hagelsteen is dus \(v_t = 15.7\) m/s.
14.2. Opties voor onderzoek#
In dit open onderzoek zijn er diverse mogelijkheden:
Onderzoek naar het vallen van een waterdruppel (of andere vloeistof)
Onderzoek naar het vallen van een balletje in een vloeistof
Onderzoek naar het vallen van een voorwerp, zoals een pingpongbal.
Onderzoek 1 is hieronder verder uitgewerkt. Voor onderzoek 2 hebben we een opstelling met buizen van verschillende diameters. Belangrijk is dat de diameter van de buis van invloed kan zijn op de beweging van het balletje. Het balletje duwt immers de vloeistof langs het balletje omhoog, zie Figuur 14.5. Onderzoek 3 kan uitgevoerd worden met de opstelling die gebruikt is bij de bepaling van \(g\), eventueel aangevuld met het gebruik van een hogesnelheidscamera.
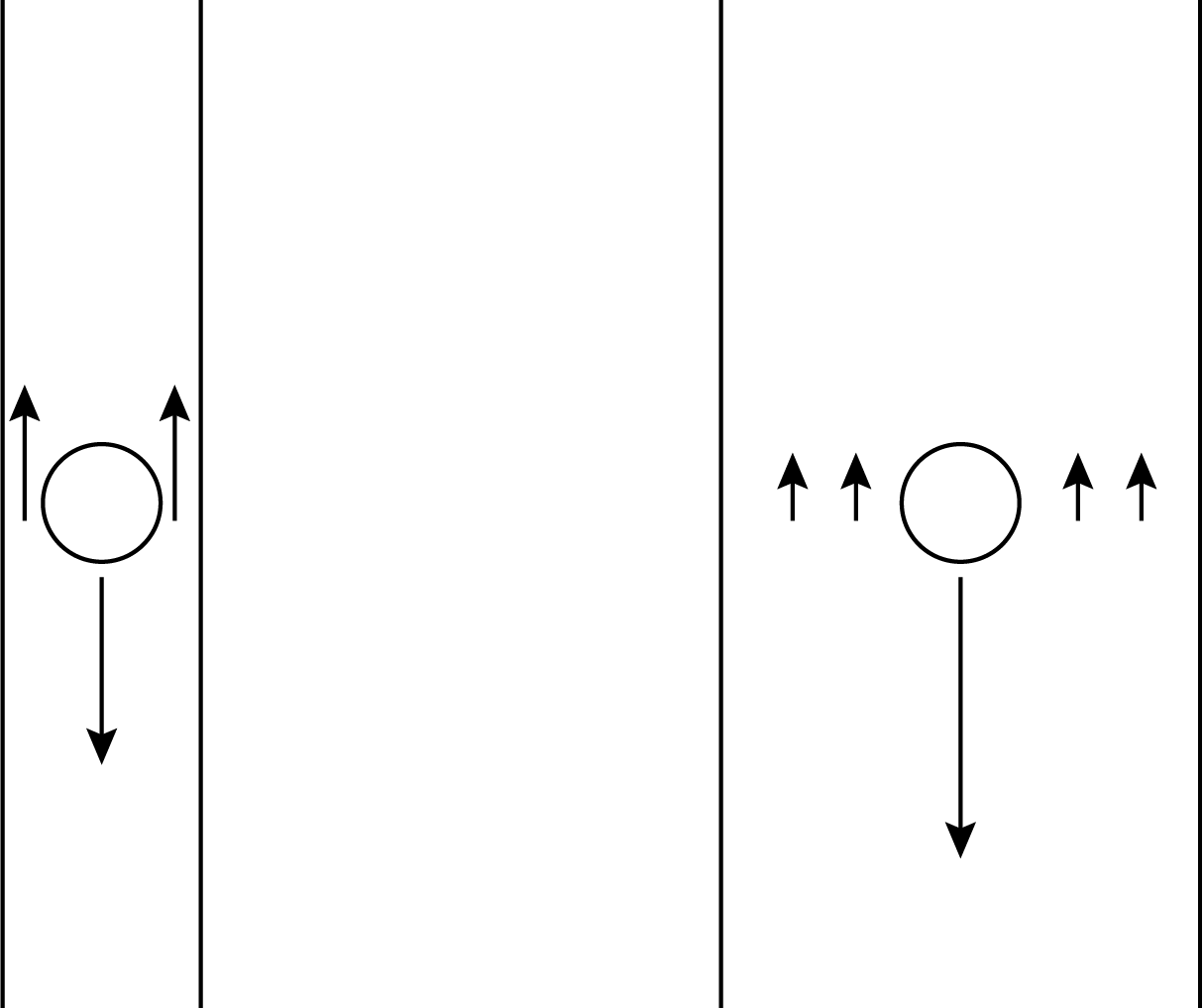
Fig. 14.5 De diameter van de buis heeft invloed op de valsnelheid van het balletje doordat de vloeistof zelf ook meer in beweging komt.#
14.3. Val van een waterdruppel#
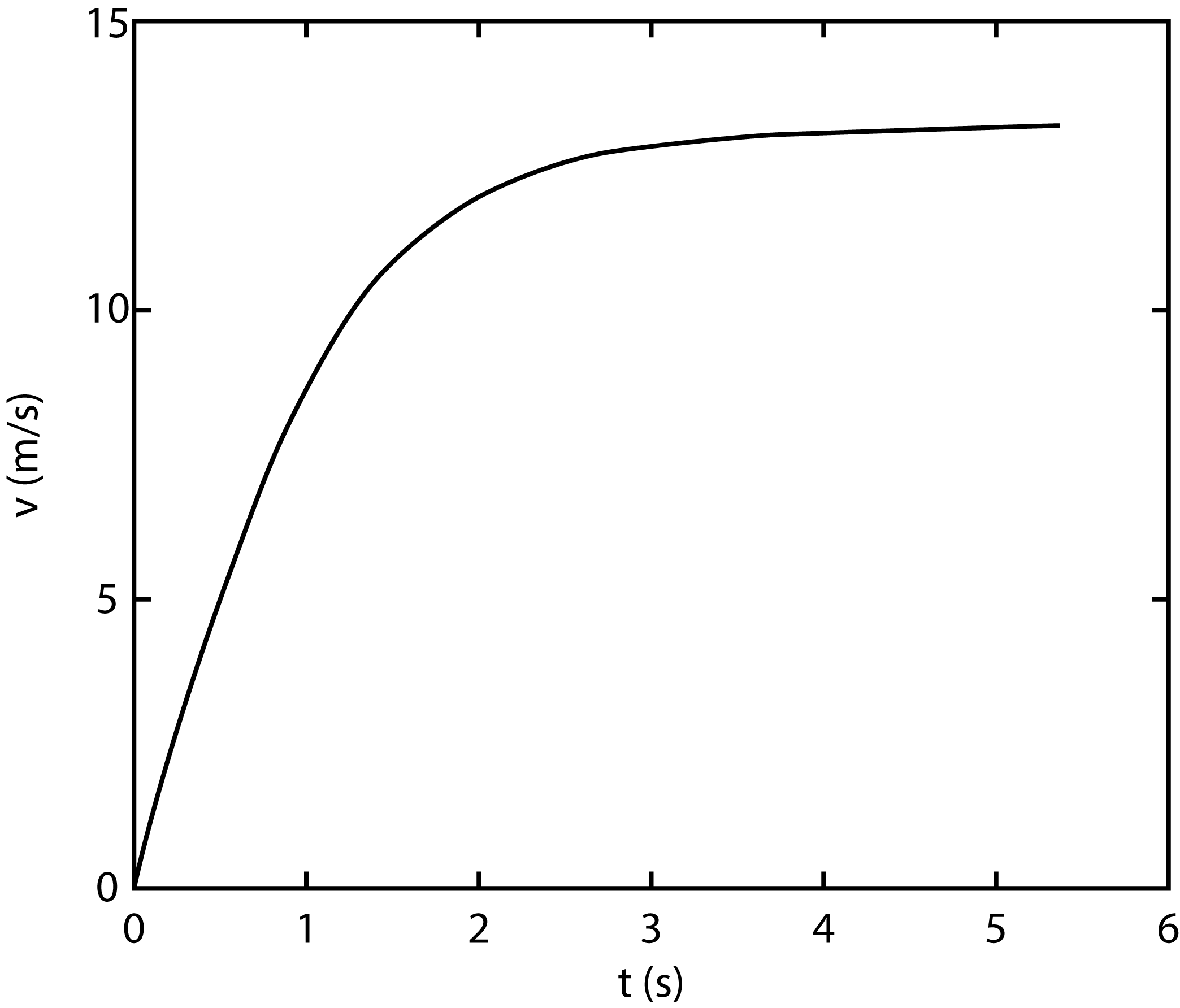
Fig. 14.6 De snelheid van een vallende waterdruppel in lucht als functie van de valtijd. De diameter van de druppel, hier bolvormig genomen, is 6 mm. Na circa 4 s is de eindsnelheid vrijwel bereikt. De getoonde curve is het exacte resultaat en is verkregen door numerieke integratie van verg. (14.6).#
Regendruppels vallen vanaf een behoorlijke hoogte. Doordat er wrijving in het spel is, gaan de druppels uiteindelijk niet dwars door het dak heen (gelukkig maar). Een aardigheidje om te weten is dat een deel van de waterdruppel ook al verdampt voordat deze de grond raakt. Om eigenschappen van regendruppels te onderzoeken, wenden we ons tot Newton.
14.3.1. Bewegingsvergelijking#
De tweede wet van Newton geeft de bewegingsvergelijking voor een vallend object:
Voor een waterdruppel die valt door de lucht, kunnen we \(F_{opw}\) verwaarlozen. Door gebruik te maken van verg. (14.2) en met \(\beta = C_D A_{\perp}\rho/2\) kan verg. (14.5) dan worden herschreven tot:
Deze schrijfwijze suggereert dat de parameter \(\beta\) constant is. In dat geval zou de wrijvingskracht evenredig zijn met het kwadraat van de snelheid. Zoals we al hebben gezien is dit echter in het algemeen niet het geval, omdat \(C_D\) nog van het Re-getal afhangt. Verg. (14.6) is een niet-lineaire (en daardoor moeilijk oplosbare) differentiaalvergelijking in de snelheid van de druppel.
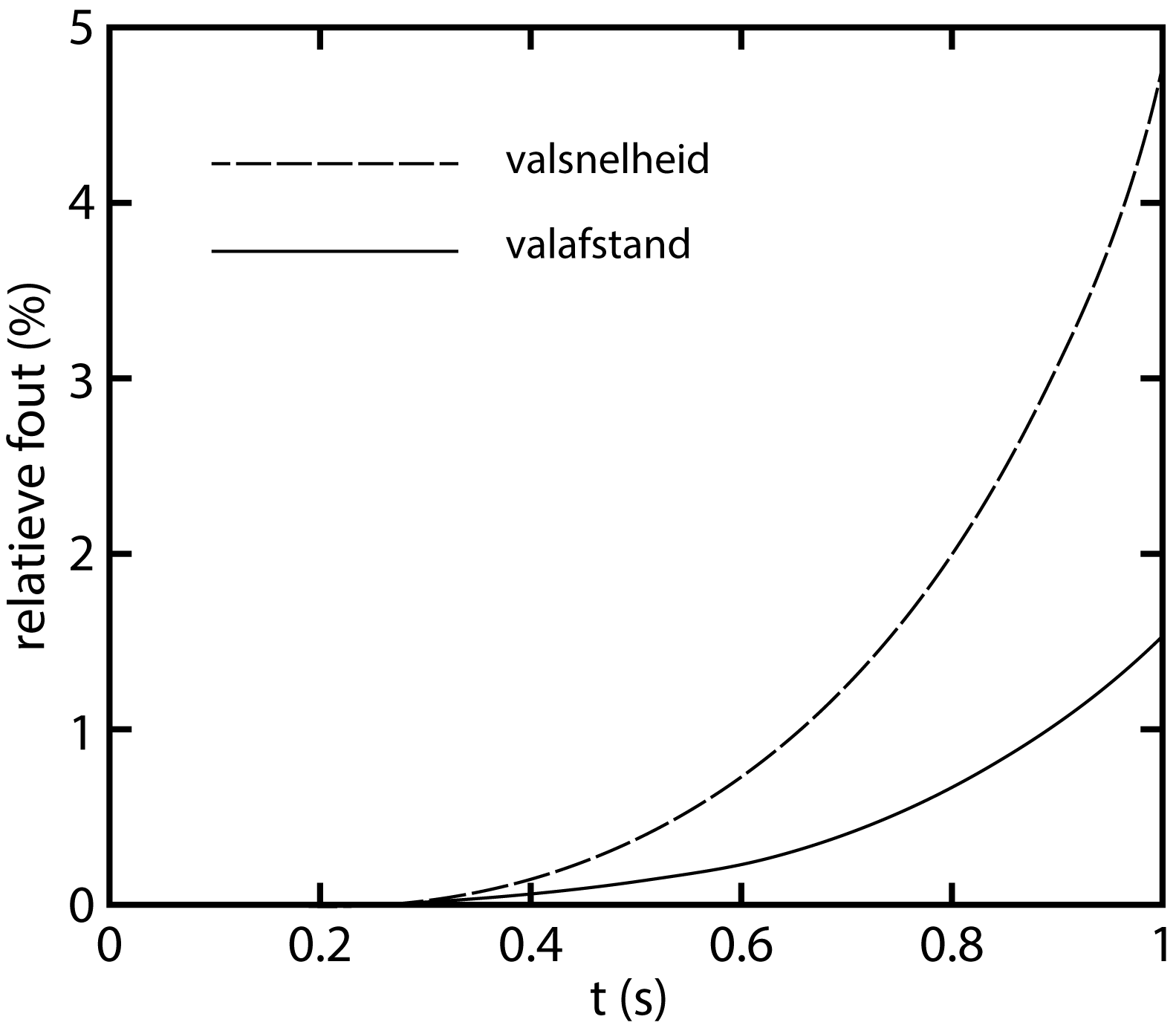
Fig. 14.7 De relatieve fout in de valsnelheid en de valafstand van de waterdruppel ten opzichte van het exacte resultaat, als het effect van luchtwrijving alleen in eerste orde wordt meegenomen. Voor beide curves geldt: diameter van de bolvormige druppel is 6 mm.#
Om het gedrag van de snelheid te illustreren, is in Figuur 14.6 de exacte oplossing van verg. (14.6) geplot voor een situatie die representatief is voor deze situatie. Hierin is meegenomen dat \(\beta\) van de snelheid afhangt, via \(C_D\). Deze oplossing is verkregen met numerieke technieken. In de figuur is te zien dat de druppel na circa vier seconden vrijwel de eindsnelheid van 12.9 m/s heeft bereikt. Dat is precies de waarde \(v_{t} = \sqrt{mg/\beta}\) die uit verg. (14.6) volgt voor \(F_D\)=0.4 N.
Een benaderde oplossing van verg. (14.6) kan worden verkregen op de volgende globaal geschetste manier. Integreren van verg. (14.6) geeft
Hiermee zijn we nog niet veel opgeschoten, want we hebben \(v(t)\) uitgedrukt in een integraal van een functie van \(v(t)\), en die is juist onbekend. Echter, door de uitdrukking voor \(v(t)\) herhaaldelijk “in zichzelf” in te vullen en door aan te nemen dat \(\beta\) tijdsonafhankelijk is, kan de volgende benadering voor de valsnelheid \(v(t)\) gevonden worden:
De vier termen in de uitdrukking voor \(v(t)\) zijn respectievelijk de beginsnelheid, de vrije val term, de eerste orde correctie en de tweede orde correctie. Uit verdere theorie volgt dat de eerste orde correctie voldoende is, mits \(t < 0.7\) s. In dat geval is de tweede orde correctie namelijk verwaarloosbaar klein ten opzichte van de eerste orde correctie.
In Figuur 14.7 zijn curves geplot voor de valsnelheid en de valafstand, die de gemaakte fout aangeven ten opzichte van het exacte resultaat als alleen de eerste orde term in verg. (14.7) wordt meegenomen. Hierbij is voor de eerste orde term \(C_D\) = 0.4 genomen, de constante waarde als gebruikt voor Figuur 14.2, die geldt voor een bolvormige druppel. Bij een maximale valtijd van ongeveer 0.6 s, is de gemaakte fout kleiner dan 1\(\%\) voor de valsnelheid en kleiner dan 0.3\(\%\) voor de valafstand. Merk op dat de grotere waarden van \(C_D\), die zullen optreden voor de kleinere snelheden in het begin van het valtraject, blijkbaar geen rol van betekenis spelen.
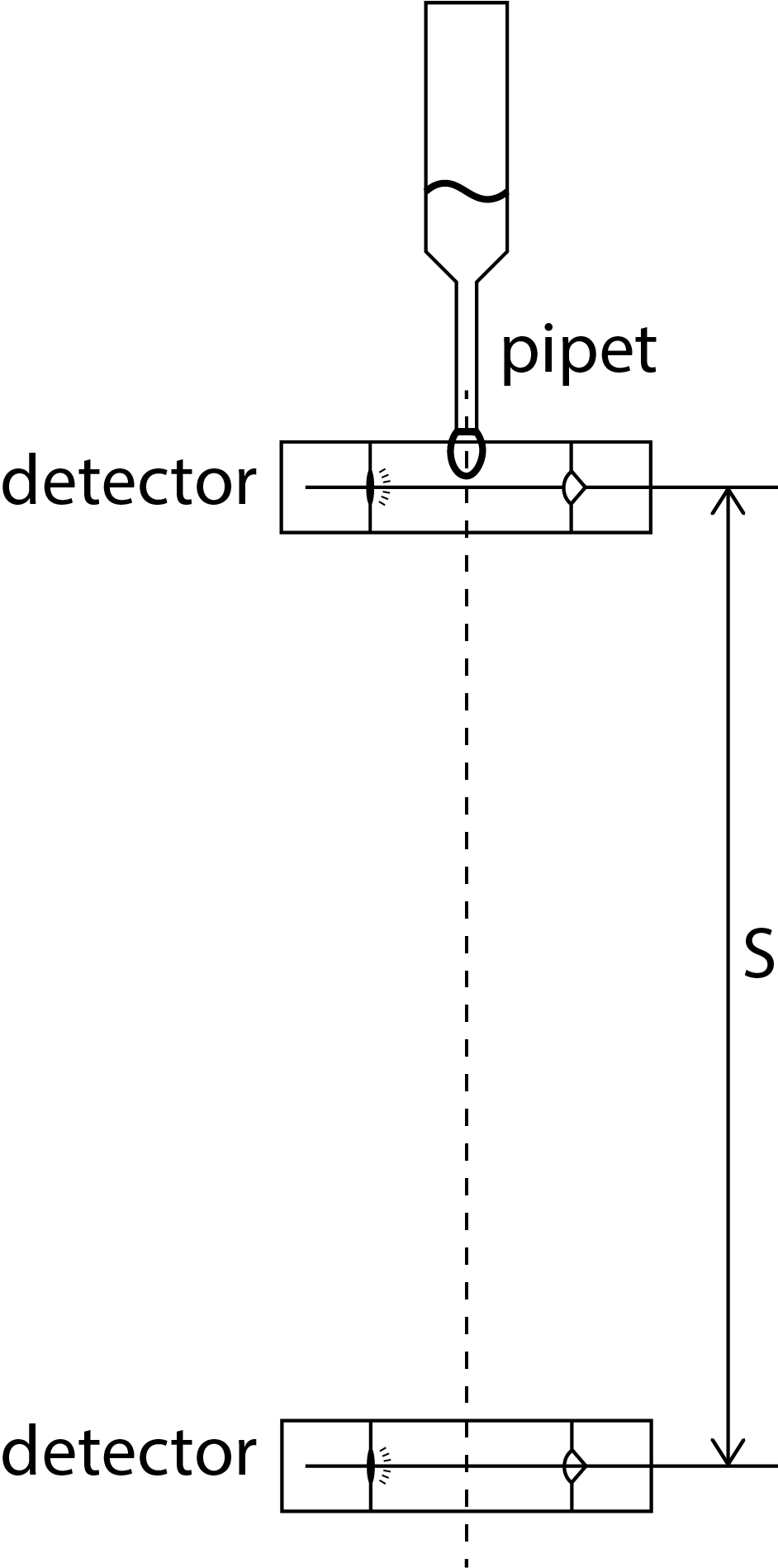
Fig. 14.8 Schematische voorstelling van een opstelling die gebruikt kan worden om de drag coëfficient van een vallende waterdruppel te bepalen. De druppel wordt gevormd met behulp van een pipet. Twee optische detectoren meten de tijd die de druppel erover doet om de afstand \(s\) te overbruggen. De detectoren bestaan uit een laser en een fotodiode, die samen een lichtsluis vormen. Wanneer een druppel door zo’n lichtsluis valt, wordt de laserstraal even onderbroken, wat een puls geeft in het signaal van de fotodiode. Een teller waarop de twee lichtsluizen zijn aangesloten meet het tijdverschil tussen de twee pulsen. De afstand tussen de twee detectoren kan worden gevarieerd.#
Integreren van Vgl. (14.7) geeft, onder verwaarlozing van de tweede orde correctie:
waarin \(s_0\) de afgelegde weg is bij \(t=0\). Als we een situatie kunnen creëren waarin bij \(t=0\) zowel de afgelegde weg als de snelheid nul zijn, dan volgt uit Vgl. (14.8):
In woorden staat hier dat de valafstand in lucht op ieder moment is gereduceerd t.o.v. de valafstand bij een vrije val met een hoeveelheid die evenredig is met de valtijd tot de vierde macht. De evenredigheidsconstante bevat de parameter \(\beta\), die zelf weer evenredig is met \(C_D\). Aan de hand van deze vergelijking kan een experiment worden bedacht waarbij bijvoorbeeld \(C_D\) voor een vallende waterdruppel wordt bepaald. In Figuur 14.8 is een voorbeeld van een opstelling weergeven die hiervoor gebruikt kan worden (en bij het practicum aanwezig is).
14.3.2. Visualisatie#
Vraag iemand een druppel te tekenen, en tien tegen één dat hij of zij de vorm van een traan tekent: aan de onderkant dik en aan de bovenkant uitlopend in een punt. Maar, een vallende waterdruppel is eerder plat dan langwerpig en lijkt daarmee op een “M&M”. Om de vorm van een vallende druppel vast te stellen en om het loodrechte oppervlak \(A_{\perp}\) te bepalen, en daaruit de weerstandscoëfficiënt \(C_D\), kun je de druppel fotograferen. Daartoe laat je de druppel zweven door deze in een opwaartse luchtstroom te plaatsen in een opstelling zoals schematisch weergegeven in Figuur 14.9.
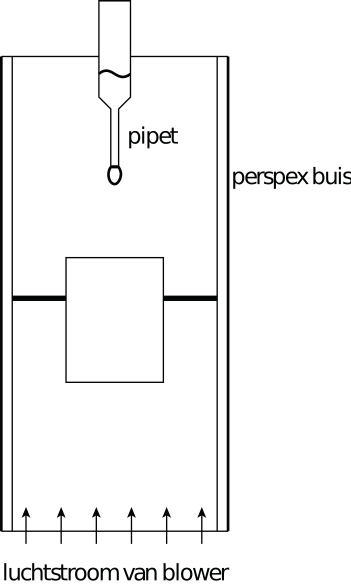
Fig. 14.9 Schematische weergave van een opstelling om een druppel te laten zweven. De opstelling bestaat uit een pipet, een perspex buis, een gaasje om de druppel tegen te houden en een blower. De voedingsspanning van de blower, en daarme de sterkte van de geproduceerde luchtstroom, is instelbaar. Met een camera kan de zwevende druppel gefotografeerd worden om zo de vorm van de druppel te bepalen.#
LET OP!
Een belangrijk verschil tussen de meting aan de massa van de druppel tijdens de valproef, de meting aan de massa door deze te druppelen en de zwevende druppel in de luchtkolom is de aanwezigheid van de wrijvingskracht bij de laatste. Dit kan gecorrigeerd worden met behulp van een schaalfactor. De schaalfactor \(\alpha\) wordt gedefinieerd door het volume van de vallende druppel te relateren aan dat van de zwevende druppel:
Dit laat zich vertalen naar
Hierin is \(m_{vallend}\) de massa van de vallende druppel en \(\rho_w\) dichtheid van water. \(D\) en \(h\) zijn respectievelijk de lange en korte as van de ellips die zichtbaar is in de foto van de druppel.
14.3.2.1. Tips bij het fotograferen#
Om een zwevende druppel goed te kunnen fotograferen heb je licht nodig. Veel licht zelfs aangezien de druppel snel door het beeld beweegt, zelfs in zwevende modus. Een scherper beeld krijg je met een kleine sluitertijd (belichtingstijd), de druppel ‘bevriest’ de druppel in beeld. Om een zo goed mogelijke opname te krijgen, moeten we zo min mogelijk beslissingen automatisch aan de camera over laten. Daarom is de aanwezige camera ingesteld op manual met een sluitertijd van 1/320 ste seconde, een diafragma van f9, en een iso waarde van 400. De flitser is uit.
Let op dat ook scherpstellen met de hand moet worden gedaan. Kies de grootste lenslengte (in dit geval 55mm) en stel scherp op de naald van het pipet. Schuif de camera zo dicht mogelijk naar de opstelling zodat je nog net scherp kan stellen.
Door een beetje diagonaal te fotograferen heb je in de achtergrond een lichtvlek van een van de lampen dit geeft een prima contrast om de omtrek van de druppel te kunnen bepalen. Houd de ontspanknop ingedrukt terwijl je de pipet rustig laat druppelen dit geeft de beste kans op een bruikbaar beeld. Let op dat de druppel naar de camera toe kan komen of er vanaf kan zweven. In het beeld is de pipetnaald dan wel scherp maar de druppel niet, dit kan dus bijdragen aan de meetonzekerheid.
14.4. Materialen#
pipetten met verschillende diameter
beschreven opstellingen
pingpongbal
piepschuim balletjes
