21. Slingers

Er zijn veel verschillende soorten slingers. Collega Ruud Brouwer schreef daar eerder al eens over. Ook bij het vak MechaRela komen slingers (en simulaties daarvan) aan bod. We bekijken hieronder een aantal verschillende soorten.

21.1. Mathematische slinger

De mathematische slinger, bestaande uit een puntmassa die slingert aan een massaloos koord, is wellicht de bekendste slinger onder de slingers. Al op de middelbare school wordt geleerd dat de periode van de slinger, weergegeven in Figuur 21.1, gegeven wordt door:

(21.1)\[ T = 2\pi \sqrt{\frac{l}{g}} \]

Hierin is \(l\) de lengte van de slinger in m en \(g\) de zwaartekrachtsversnelling in m/s\(^2\). De hoek waarmee de slinger slingert lijkt er niet toe te doen. Echter, dit komt doordat bij deze gebruik gemaakt is van de kleine hoekbenadering (\(sin(\theta)=\theta\)). Ook wrijving is in deze vergelijking verwaarloosd. In het algemeen kunnen we gebruik maken van de bewegingsvergelijking:

(21.2)\[ m l \frac{d^2\theta}{dt^2} + 2 m \gamma \frac{d\theta}{dt}= m g sin(\theta) \]

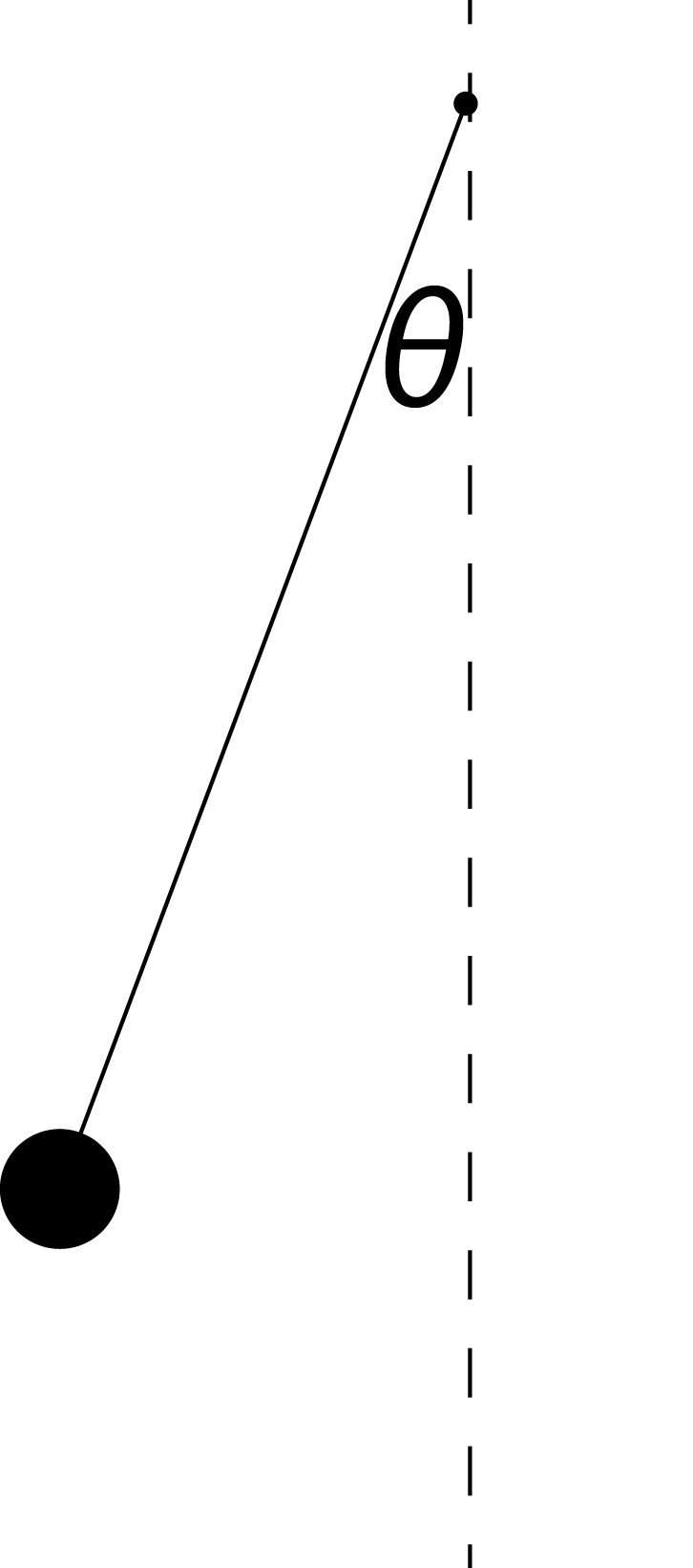
Fig. 21.1 De ‘eenvoudige’ mathematische slinger bestaat uit een dun koord met een puntmassa, waarbij de massa heen en weer slingert.

waarin \(\theta\) de hoek is tussen de slinger en de verticaal (zie Figuur 21.1). Hierin veronderstellen we dus ook dat wrijving een rol speelt: deze wordt beschreven door de constante \(\gamma\). Hierbij kunnen we nog een aantal simplificaties uitvoeren die ons helpen in het begrijpen en oplossen van de beweging:

• wrijving verwaarlozen

• de kleine hoekbenadering toepassen

Bij het verwaarlozen van wrijving kunnen we de vergelijking oplossen met een elliptische integraal en verkrijgen we de oplossing:

(21.3)\[ T = 2\pi \sqrt{\frac{l}{g}} \left[1+\left(\frac{1}{2}\right)^2sin^2\left(\frac{\alpha}{2}\right)+\left(\frac{1\cdot3}{2\cdot4}\right)^2sin^4\left(\frac{\alpha}{2}\right)+... \right] \]

Een goede benadering daarvan, wordt volgens Kidd & Fogg (2002):

\[ T = 2\pi \sqrt{\frac{l}{gcos(\theta/2)}}\]

Als we de hoek klein houden maar demping mee nemen, dan vinden we een algemene oplossing:

(21.4)\[ \theta(t) = A e^{r_1 t} + B e^{r_2 t} \]

Als we deze algemene oplossing in verg. (21.2) stoppen, dan kunnen we waardes voor \(A\), \(B\), \(r_1\) en \(r_2\) afleiden.

Laat je de slinger heel lang slingeren, dan zul je zien dat de slinger niet meer in hetzelfde vlak blijft draaien. De rotatie van de aarde wordt dan zichtbaar gemaakt m.b.v. de slinger. Dit staat ook wel bekend als de slinger van de Foucault.

Daarnaast heb je natuurlijk de mogelijkheid om onder je eerste slinger een tweede slinger te hangen, zie Figuur 21.2. Dit is dan een gekoppelde slinger. De gekoppelde slinger is een voorbeeld van een chaotisch systeem.

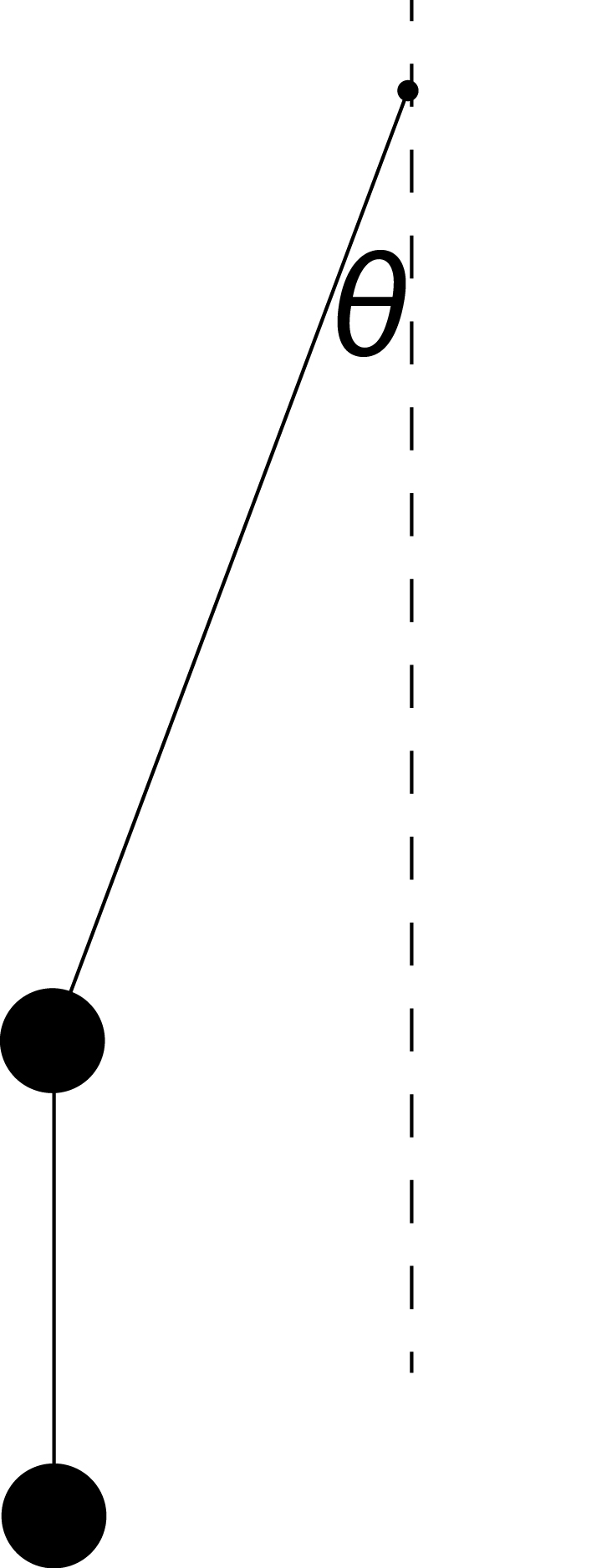
Fig. 21.2 De dubbele slinger is een voorbeeld van een chaotisch systeem

Naast het onder elkaar hangen van slingers, heb je ook de mogelijkheid om de slingers naast elkaar te hangen. Dit gekoppelde systeem is een ‘aangedreven’ systeem waarbij de slinger die eerst niet synchroon slingeren uiteindelijk wel synchroon gaan slingeren.

21.2. Fysische slinger

Bij een fysische slinger wordt het model van een massalooskoord met daaraan een puntmassa los gelaten. Het object heeft nu echt massa en daarmee een traagheidsmoment waarbij niet alleen de traagheid van de puntmassa mee genomen wordt. De bewegingsvergelijking wordt dan afgeleid uit:

(21.5)\[ I\frac{d^2 \theta}{d t^2} = -r_z m g sin(\theta) \]

21.3. Bifilaire slinger

Een bifilaire slinger is een staaf (of voorwerp) hangend aan twee draden met lengte \(h\) en onderlinge afstand \(d\). De periode hangt zowel af van beide factoren. Deze afhankelijkheid van \(h\) en \(d\) zou op basis van MGO kennis zelfstandig af te leiden moeten zijn,

Een variant hier op is het maken van bifilaire slinger met behulp van een hoolahoop, zie The Physics Teacher, Vol. 51, October 2013, p.418-419.

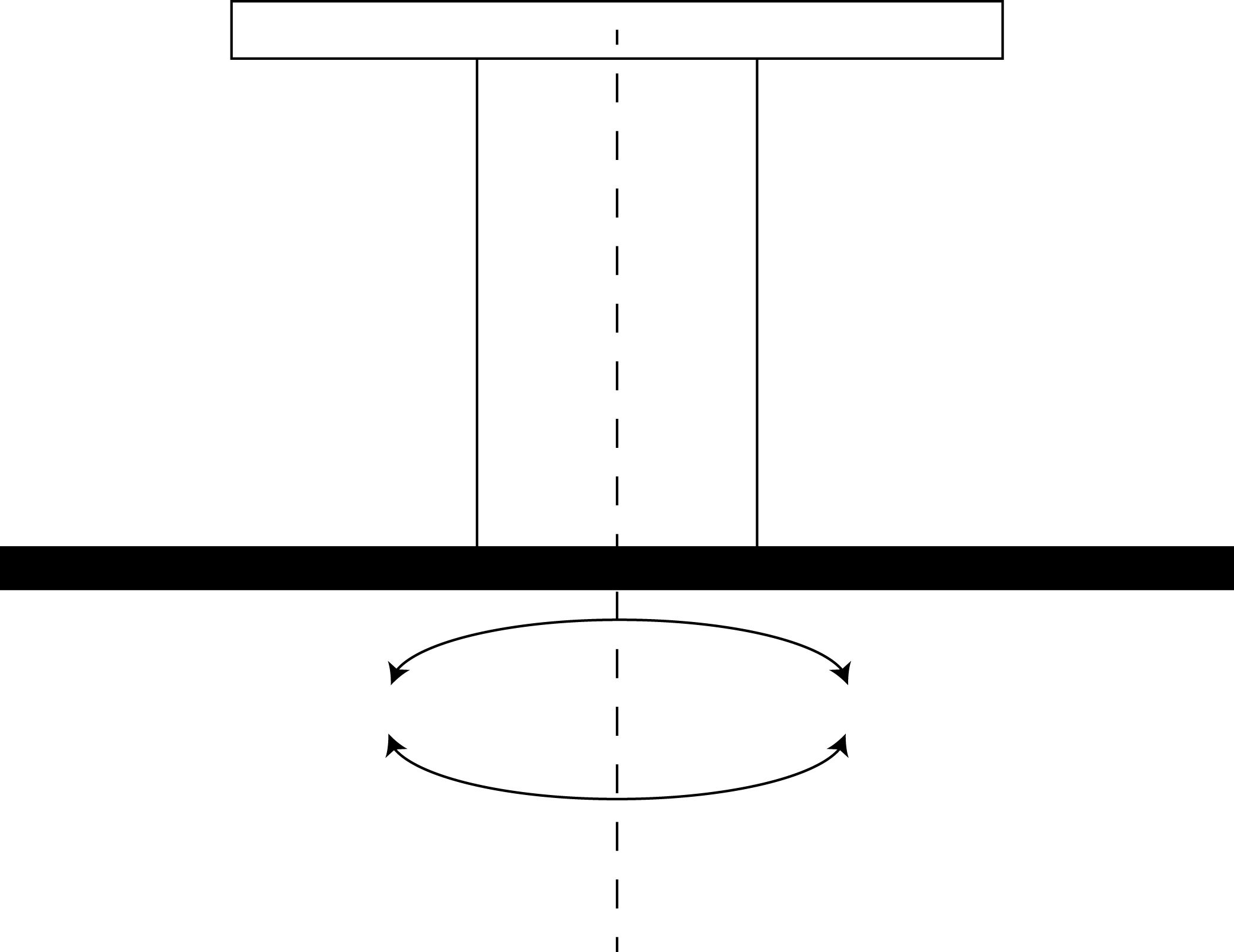
Fig. 21.3 De biffilaire slinger

21.4. Torsieslinger

Een lichaam dat we ophangen aan een dun koord kunnen we laten roteren om de y-as, zie Figuur 21.4. De trillingstijd van zo’n torsieslinger wordt gegeven door:

(21.6)\[ T = 2\pi \sqrt{\frac{2 I l}{\pi G R^2}} \]

Hierin is \(I\) het traagheidsmoment van het opgehangen object in Nm\(^2\), \(l\) de lengte van de draad, \(G\) de glijdingsmodulus van het draadmateriaal in N/s\(^2\). en \(R\) de straal van de rond veronderstelde draad in m.

Fig. 21.4 De torsieslinger bestaat uit een object opgehangen aan een dun koord, het object draait om de y-as.

21.5. Besselslinger

Zie deze beschrijving of dit artikel.

21.6. Kegelslinger

Een kegelslinger is een slinger die aangedreven wordt door een elektromotor, zie Figuur 21.5. De slinger draait in dit geval rond (beschrijft een kegel), waarbij de hoek met de verticaal afhankelijk is van de snelheid en daarmee de periode. De bijbehorende bewegingsvergelijking is eenvoudig af te leiden op basis van VWO natuurkunde, maar daarom niet minder interessant om te onderzoeken.

Fig. 21.5 De kegelslinger