24. Stroming door leidingsystemen

Bijdrage geleverd door dr. ir. Martin Rohde, o.a. docent tweedejaars Fysische transportverschijnselen.

24.1. Inleiding

In veel industriële toepassingen worden leidingsystemen gebruikt, zie Figuur 24.1. Deze leidingen dienen er voor om bijvoorbeeld olie en gas over honderden kilometers te verpompen, reactanten van een opslagtank naar een chemische reactor te leiden, water vanaf de duinen tot aan je keukenkraan te brengen en koelvloeistof, benzine en olie door een automotor te laten stromen. Het zal je dan ook niet verbazen dat er in de afgelopen decennia veel onderzoek naar leidingsystemen is gedaan.

Fig. 24.1 Een voorbeeld van een (gedeelte van een) leidingsysteem

De stroming door leidingsystemen is zeer complex, zeker als de stroomsnelheid van de vloeistof of gas en de diameters van de leidingen groot zijn. Onder deze condities wordt de stroming turbulent (dit in tegenstelling tot laminaire stroming). Turbulente stroming is een chaotisch fenomeen waar nog steeds heel veel onderzoek aan verricht wordt. Nog altijd bestaat er geen directe oplossing voor het stromingsveld als functie van plaats en tijd, beschreven met de Navier-Stokes vergelijking. Men moet dus lange berekeningen uitvoeren om de snelheden en drukken uit te kunnen rekenen. Figuur 24.2 is een mooi voorbeeld van hoe zo’n stromingsprofiel er uit ziet, gemaakt met behulp van Computational Fluid Dynamics.

Fig. 24.2 Turbulente stroming in een buis. Uit: Jeong, J., Hussain, F.: On the identification of a vortex. J. Fluid Mech.285, 69–94 (1995)

Gelukkig is er ook een andere benadering mogelijk. Deze benadering valt onder de technische stromingsleer. In dit hoofdstuk zal deze benadering nader worden uitgelegd. Daarna kun je de theorie direct toepassen in de praktijk, waarbij je een onderzoeksvraag bedenkt, een opstelling maakt waarmee je de vraag hopelijk kunt beantwoorden en het onderzoek ook zelf uitvoert.

24.2. Balansen

In de praktijk is men meestal niet geïnteresseerd in de details in de stroming in een leiding. Wel interessant zijn antwoorden op vragen als: wat voor pomp moet ik installeren om 1 kubieke meter water te pompen over een leiding met een diameter van 50 centimeter, met een lengte van 100 meter en met over een hoogteverschil van 20 meter? Of: welk debiet (in m\(^3\)/s) kan ik door een leiding pompen met een bepaalde pomp? Welke bocht heb ik nodig om niet teveel drukverschil (en dus verlies) te krijgen?

Om op deze vragen antwoord te kunnen geven kijken we niet zozeer naar de stroming, maar bijvoorbeeld naar de hoeveelheid mechanische energie die een leiding instroomt en de naar hoeveelheid die de leiding weer verlaat. Of naar de hoeveelheid massa die de buis instroomt en weer uit stroomt. Met andere woorden, we stellen een balans op.

Vergelijk een balans met je bankrekening. In stationaire toestand, d.w.z. als je saldo constant blijft, luidt de balans:

\[StuFie + Salaris bijbaan = Uitgaven.\]

Ofwel, wat er in komt gaat er ook weer uit.

24.2.1. Massabalans

Een van de eenvoudigste balansen in de stromingsleer is die van massa. De hoeveelheid massa die de buis instroomt op punt 1 in Figuur 24.3, moet er ook weer uitstromen op punt 2:

\[ \phi_{m_1} = \phi_{m_2} \]

Hierin is \(\phi_{m}\) de massa die door een bepaald punt stroom in kg/s, gegeven door \(\phi_{m}=\rho A v\), met \(\rho\) de dichtheid in kg/m\(^3\), \(A\) het doorstromend oppervlak (van de buis) in m\(^2\) en \(v\) de stroomsnelheid in m/s. Omdat de diameter van de buis op punt 2 kleiner is, water onsamendrukbaar is (dichtheid blijft grofweg gelijk) zal het water op punt 2 sneller moeten stromen. Wanneer er geen verliezen optreden, kunnen we de snelheid van het water op punt 2 uitrekenen op basis van de massabalans. Echter, de werkelijke situatie is een stuk complexer.

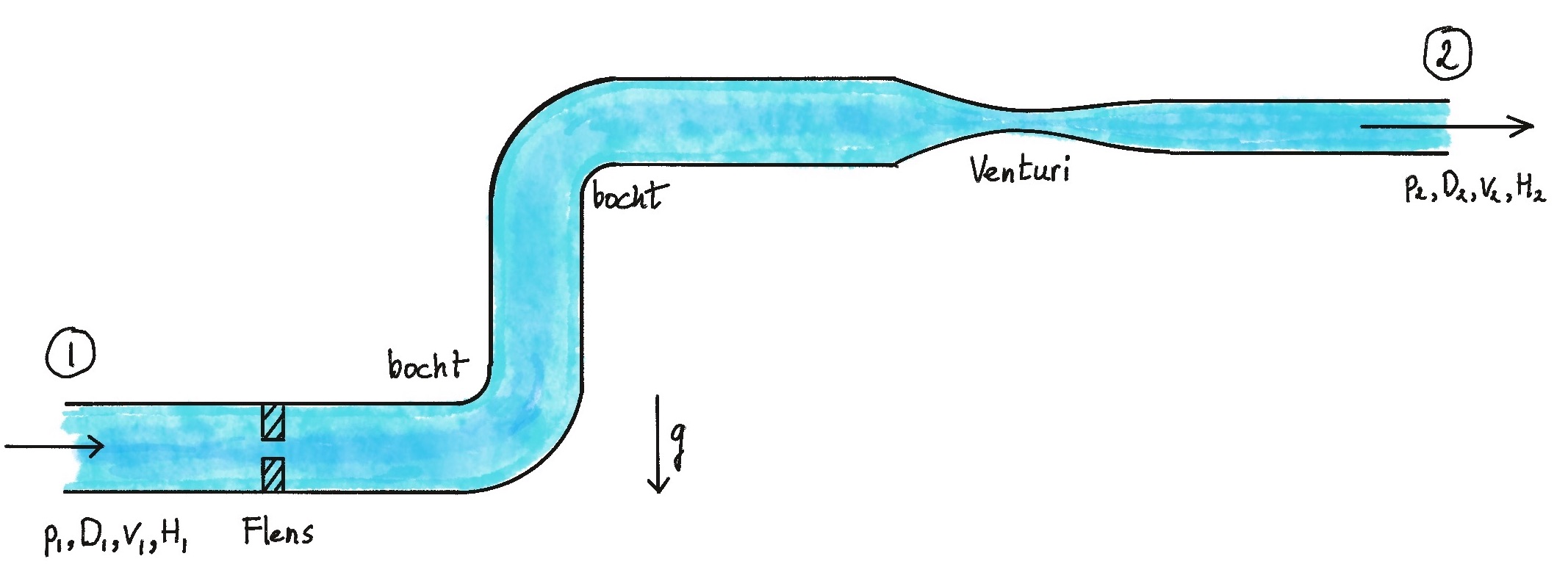
Fig. 24.3 Leidingsysteem met twee bochten en twee vernauwingen. Bij de in- en uitgang van de leiding zijn de drukken \(p\), diameters \(D\), gemiddelde vloeistofsnelheden \(v\) en hoogtes \(H\) aangegeven.

De buis in Figuur 24.3 bevat bochten, lokale vernauwingen door obstructies of dikte verandering van de buis, en varieert in hoogte. Er treden ongetwijfeld verliezen op, waardoor de snelheid van de vloeistof in punt 2 niet slechts op basis van een massabalans berekend kan worden. Om het debiet, de hoeveelheid vloeistof die per seconde door de buis stroomt, te berekenen, maken we gebruik van de energie balans.

24.2.2. Energie balans

Als water in vrije val (denk aan een waterval) naar beneden stroomt, dan is er sprake van omzetting van potentiële energie in kinetische energie. Wanneer er geen wrijving is, is de hoeveelheid mechanische energie constant. De hoeveelheid mechanische energie die een gas of vloeistof per kilogram kan bevatten is de som van de kinetische energie en de potentiële energie zoals hieronder aangegeven:

\[ e=\frac{1}{2}v^{2}+gz\ \left(\frac{J}{kg}\right). \]

Voor onze buis uit Figuur 24.3, waarbij we wrijving nog buiten beschouwing laten, stroomt er vloeistof met \(e_{1}\) J/kg aan mechanische energie het systeem binnen op punt 1 en op punt 2 stroomt deze vloeistof met \(e_{2}\) J/kg aan mechanische energie er weer uit. De hoeveelheid mechanische energie die in- en uitstroomt zijn respectievelijk

\[\begin{split} \begin{align} \phi_{e,in}=\phi_{m}\cdot e_{1}=\phi_{m}\cdot\left(\frac{1}{2}v_{1}^{2}+gz_{1}\right)\\ \phi_{e,uit}=\phi_{m}\cdot e_{2}=\phi_{m}\cdot\left(\frac{1}{2}v_{2}^{2}+gz_{2}\right) \end{align} \end{split}\]

waarbij \(\phi_{m}\) het massa-debiet in kg/s voorstelt.

Echter, heel vaak is er sprake van toevoeging van mechanisch energie door arbeid of een pomp en verlies van mechanische energie door wrijving. Deze termen zullen we moeten meenemen om uit te kunnen rekenen hoeveel mechanische energie uiteindelijk uit de leiding stroomt of hoeveel energie het kost om een vloeistof of gas door een leiding te laten stromen. Daartoe stellen we een mechanische energiebalans tussen de ingang en uitgang van de leiding op. In stationaire toestand luidt deze in woorden

\[ \text{uit}-\text{in}=\text{toevoeging door arbeid}-\text{verlies door wrijving}, \]

oftewel

\[ \phi_{m}\cdot e_{2}-\phi_{m}\cdot e_{1}=W'+\phi_{pomp}-\phi_{fr}. \]

De termen \(W'\), \(\phi_{pomp}\) en \(\phi_{fr}\)worden hieronder toegelicht.

24.2.3. Arbeid (\(W'\) en \(\phi_{pomp}\))

Als in Figuur 24.3 de drukken bij de in- en uitgang ongelijk zijn dan wordt er netto arbeid per seconde verricht op de vloeistof in de leiding ter grootte van \(W'=p_{1}A_{1}v_{1}-p_{2}A_{2}v_{2,}\) waarin \(A\) het doorstroomd oppervlak van de leiding is (bij een ronde buis \(A=\frac{1}{4}\pi D^{2}\)). Hierin zijn het product \(p\cdot A\) de kracht die op dat doorstroomd oppervlak werkt en \(v\) de verplaatsing per seconde. Als we deze uitdrukking iets omschrijven dan kunnen we de arbeid per seconde uitdrukken in termen van massadebiet:

\[ W'=\frac{p_{1}}{\rho}\underbrace{\rho A_{1}v_{1}}_{=\phi_{m}}-\frac{p_{2}}{\rho}\underbrace{\rho A_{2}v_{2}}_{=\phi_{m}}=\phi_{m}\left(\frac{p_{1}}{\rho}-\frac{p_{2}}{\rho}\right).\]

Hierbij zijn we uitgegaan van een constante dichtheid. Een andere manier om mechanische energie toe te voegen aan een leidingsysteem is het plaatsen van een pomp. Deze toevoeging wordt aangegeven met \(\phi_{W}\ \left(\frac{\textrm{J}}{\textrm{s}}\right)\).

24.2.4. Wrijving met de wand (\(\phi_{fr}\))

Naast het toevoegen van mechanische energie is er meestal ook sprake van verlies. Het laten stromen van een vloeistof door een rechte, horizontale buis kost energie; probeer maar eens heel hard door een rietje te blazen! Dit verlies aan mechanische energie wordt veroorzaakt door wrijving die de vloeistof ondervindt met het leidingsysteem zelf. Deze wrijving kan grofweg opgedeeld worden in twee categorieën: wrijving met de wand van de leiding en wrijving veroorzaakt door appendages zoals bochten, vernauwingen, kranen etc. Beide worden hier apart behandeld.

Het energieverlies door de aanwezigheid van de wanden vindt plaats omdat de wanden de vloeistof tegenhouden. De wanden staan immers stil en de vloeistof beweegt met een gemiddelde snelheid \(v\) door de leiding. Het energieverlies wordt gemodelleerd volgens \(\phi_{fr,w}=\phi_{m}e_{fr,w}=\phi_{m}\cdot4f(Re)\frac{L}{D_{h}}\cdot\frac{1}{2}v^{2}\). Hierin stelt \(Re\) het zogenaamde Reynolds-getal voor, die is gedefiniëerd als

\[ Re\equiv\frac{\rho vD_{h}}{\mu}.\]

De dynamische viscositeit, \(\mu\ \left(\textrm{Pa.s}\right)\), is een maat voor de stroperigheid van de vloeistof en \(D_{h}\) is de hydraulische diameter, \(D_{h}\equiv4A/S\), waarin \(S\) de ‘’natte omtrek’’ wordt genoemd. De natte omtrek is dat deel van de omtrek van een leiding dat contact maakt met de vloeistof. Een volledig gevulde, ronde buis heeft dus een hydraulische diameter van \(D_{h}=4\cdot\frac{1}{4}\pi D^{2}/\pi D=D\), maar voor een half gevulde, ronde buis hangt het af van de hoeveelheid vloeistof die de wand raakt (zie Figuur 24.4).

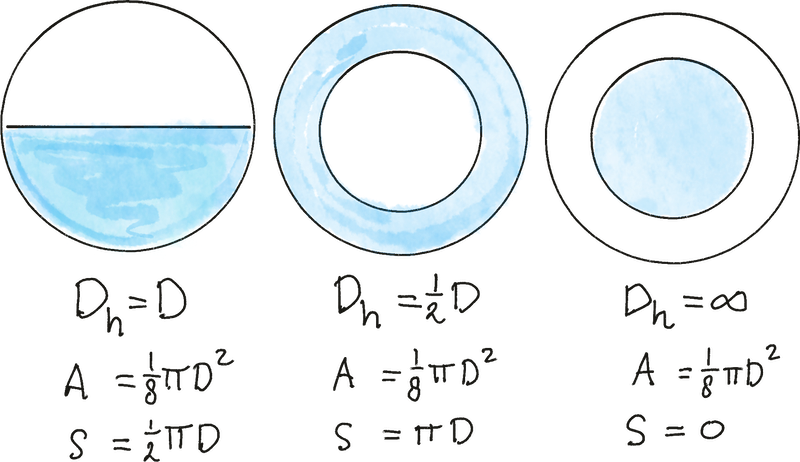
Fig. 24.4 Hydraulische diameter van drie half-gevulde, ronde leidingen. In alle gevallen stroomt er evenveel water doorheen. De blauwe kleur geeft de plaats van de vloeistof aan.

De Fanning frictiefactor \(f(Re)\) is een functie van het Reynoldsgetal en van de wandruwheid. Deze frictiefactor wordt van te voren empirisch bepaald en kan worden opgezocht in grafieken en tabellen. Ook bestaan er zogenaamde correlaties voor \(f(Re)\). Zowel de grafiek als correlaties staan aangegeven in figuur Figuur 24.7.

24.2.5. Wrijving door appendages

Appendages zoals bochten, kranen, vernauwingen e.d. veroorzaken wervels in de stroming die voor verlies van mechanische energie zorgen. Deze wervels zullen deels door viscositeit omgezet worden in warmte. Het verlies wordt op eenzelfde manier gemodelleerd als de wrijving door de wand:

\[ \phi_{fr,app}=\phi_{m}e_{fr,app}=\phi_{m}\cdot K_{app}\cdot\frac{1}{2}v^{2}.\]

De frictieconstante \(K_{app}\) is een maat voor de hoeveelheid wrijving die de appendage veroorzaakt. Ook voor deze contante bestaan correlaties. Zie Figuur 24.9.

24.2.6. Stationaire mechanische energiebalans (constante dichtheid)

Met het bovenstaande kunnen we de stationaire, mechanische energiebalans over een leidingsysteem met appendages en stukken leiding van verschillende diameters en ruwheden opstellen. Deze balans, die opgesteld is tussen de in- en uitgang van het systeem luidt:

\[\phi_{m}\cdot\left(\frac{1}{2}v_{2}^{2}+gz_{2}-\frac{1}{2}v_{1}^{2}+gz_{1}\right)=\phi_{m}\cdot\left(\frac{p_{1}}{\rho}-\frac{p_{2}}{\rho}\right)+\phi_{pomp}-\phi_{m}\cdot\left(\sum_{i}4f(Re_{i})\frac{L_{i}}{D_{h,i}}+\sum_{j}K_{app,j}\right)\cdot\frac{1}{2}v^{2}.\]

Let op dat deze balans alleen geldt voor een vloeistof of gas waarvoor de dichtheid niet verandert in het systeem. De index ‘’i’’ geeft elk apart stuk leiding weer en de index ‘’j’’ elke appendage.

24.3. Voorbeelden

24.3.1. Voorbeeld 1

Beschouw de stroming van een vloeistof door een rechte, horizontale, ronde buis (zie Figuur 24.5). Bereken de drukval die nodig is om de vereiste vloeistofsnelheid te bereiken.

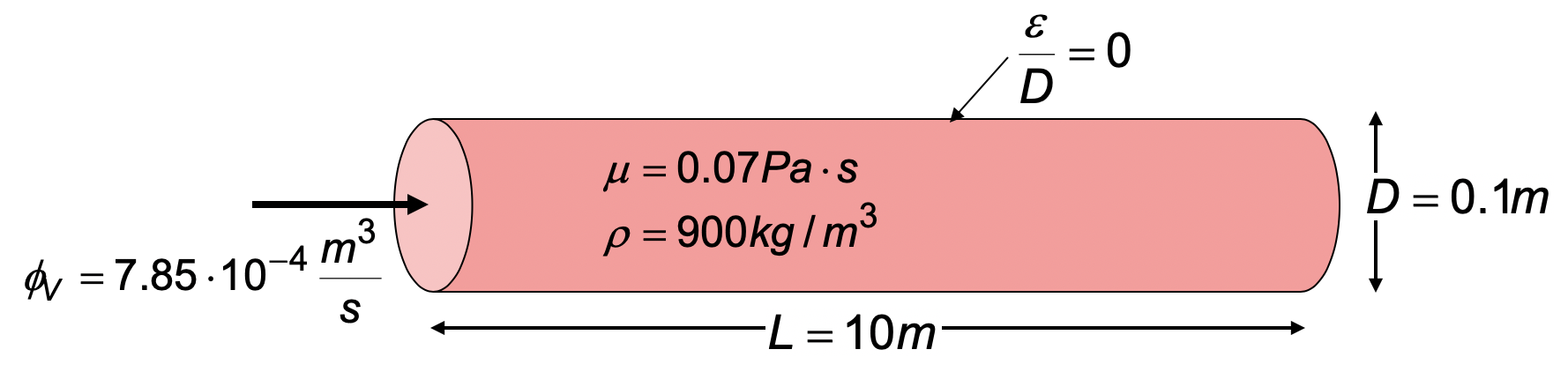
Fig. 24.5 Figuur behorende bij voorbeeld 1.

In dit geval is er geen pomp aanwezig (\(\phi_{pomp}=0\)), zijn de snelheden bij in- en uitgang gelijk aan elkaar (\(v_{1}=v_{2}\)), is de buis horizontaal (\(z_{1}=z_{2}\)) en zijn er geen appendages aanwezig. De mechanische energiebalans luidt dus:

\[ 0=\frac{p_{1}}{\rho}-\frac{p_{2}}{\rho}-4f(Re)\frac{L}{D_{h}}\cdot\frac{1}{2}v^{2}. \]

De snelheid \(v\) kan uitgerekend worden uit het volumedebiet \(\phi_{v}\) en het doorstroomd oppervlak \(A=\frac{1}{4}\pi D^{2}\), namelijk \(v=\phi_{v}/A=0.1\ m/s\). Het Reynoldsgetal is nu \(Re=\rho vD/\mu=129\) (de hydraulische diameter is \(D_{h}=D\)). In Figuur 24.7 zien we dat de correlatie bij dit Reynoldsgetal \(4f=64/Re=0.5\) is. De benodigde drukval is daarom:

\[ p_{1}-p_{2}=\rho\cdot4f(Re)\frac{L}{D_{h}}\cdot\frac{1}{2}v^{2}=900\cdot0.5\cdot\frac{10}{0.1}\cdot\frac{1}{2}0.1^{2}=225\ Pa.\]

24.3.2. Voorbeeld 2

Beschouw opnieuw een stroming van een vloeistof door een rechte, horizontale, ronde buis (zie Figuur 24.6). Nu is de drukval bekend en moet de snelheid uitgerekend worden.

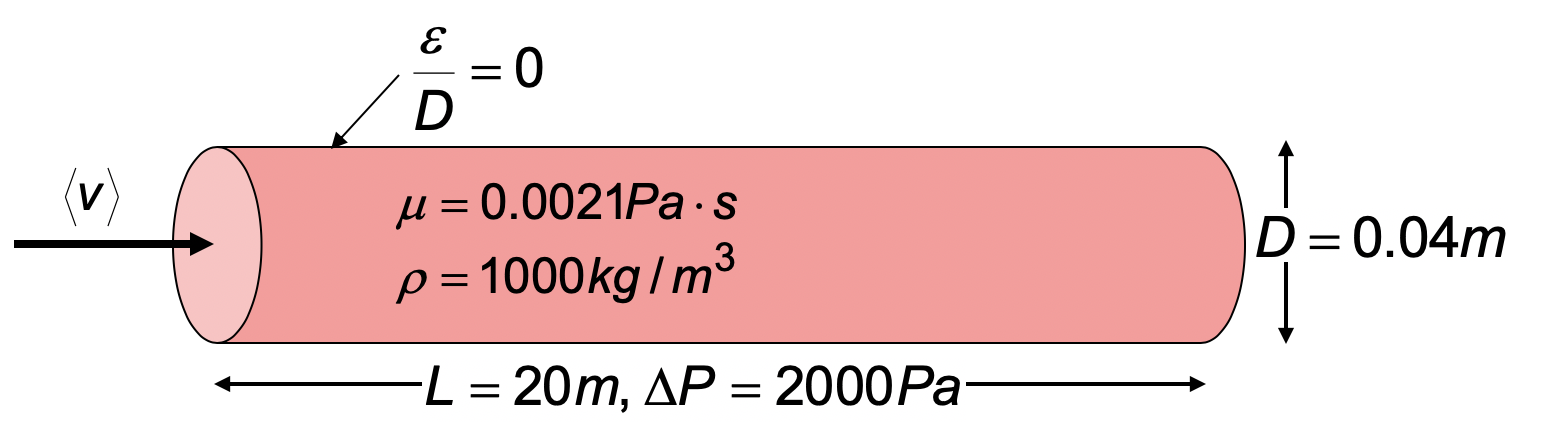
Fig. 24.6 Figuur behorende bij voorbeeld 2

Ook in dit geval is er geen pomp aanwezig (\(\phi_{pomp}=0\)), zijn de snelheden bij in- en uitgang gelijk aan elkaar (\(v_{1}=v_{2}\)), is de buis horizontaal (\(z_{1}=z_{2}\)) en zijn er geen appendages aanwezig. De mechanische energiebalans is dus hetzelfde als in voorbeeld 1. Om de snelheid te krijgen gebruiken we een correlatie voor de Fanning frictiefactor. Omdat we niet op voorhand weten wat het Reynoldsgetal is gokken we dat het de Blasius-correlatie is (later wel controleren!):

\[ p_{1}-p_{2}=\rho\cdot4f(Re)\frac{L}{D_{h}}\cdot\frac{1}{2}v^{2}=\rho\cdot0.316\left(\frac{\rho vD}{\mu}\right)^{-1/4}\frac{L}{D_{h}}\cdot\frac{1}{2}v^{2}\rightarrow \]

\[ v^{7/4}=\frac{2(p_{1}-p_{2})}{0.316}\frac{D^{5/4}}{L\mu^{1/4}\rho^{3/4}}\rightarrow v=0.50\ m/s. \]

Het Reynoldsgetal, \(Re=9523\), valt binnen het bereik waarin de Blasius correlatie gebruikt mag worden. De oplossing is dus correct.

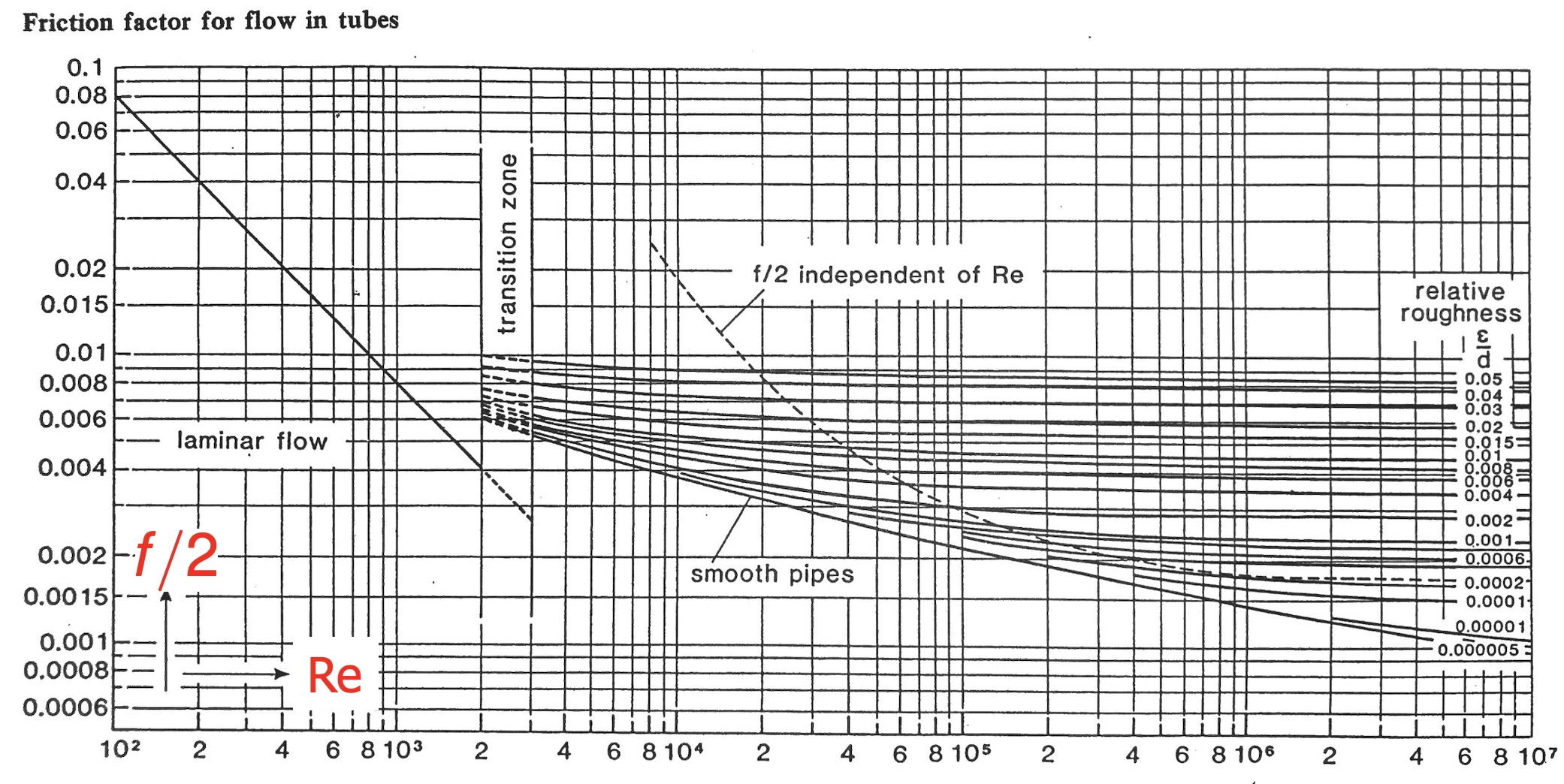
Fig. 24.7 Fanning frictie factor als functie van het Reynoldsgetal \(Re\). De wandruwheid wordt gegeven door \(\epsilon/D\), waarbij \(\epsilon\) de hoogte is van de wandruwheid. De grafiek komt uit de ``Transport Phenomena Data Companion’’ van Janssen en Warmoeskerken.

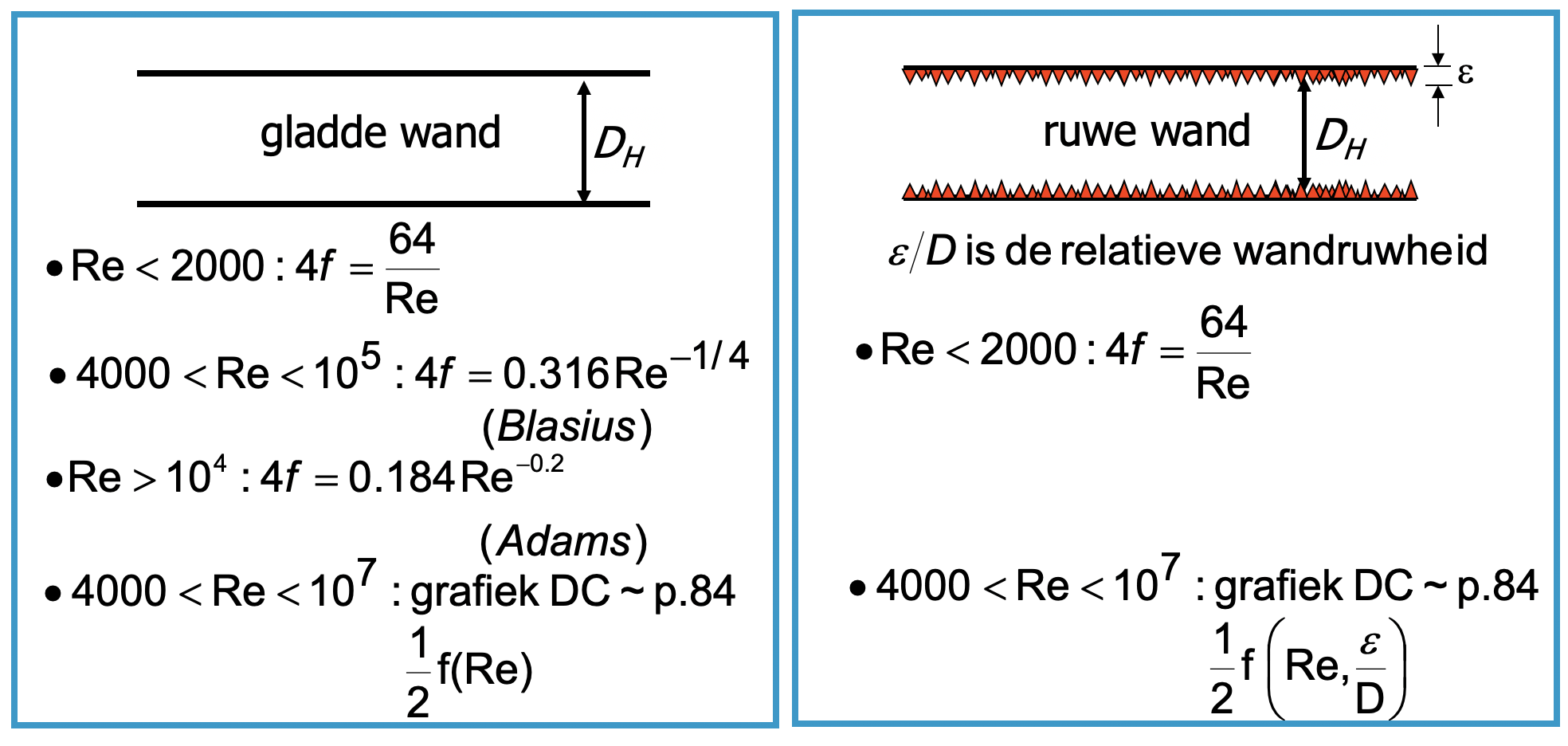
Fig. 24.8 Fanning frictie factor als functie van het Reynoldsgetal \(Re\). De wandruwheid wordt gegeven door \(\epsilon/D\), waarbij \(\epsilon\) de hoogte is van de wandruwheid. De grafiek komt uit de ``Transport Phenomena Data Companion’’ van Janssen en Warmoeskerken.

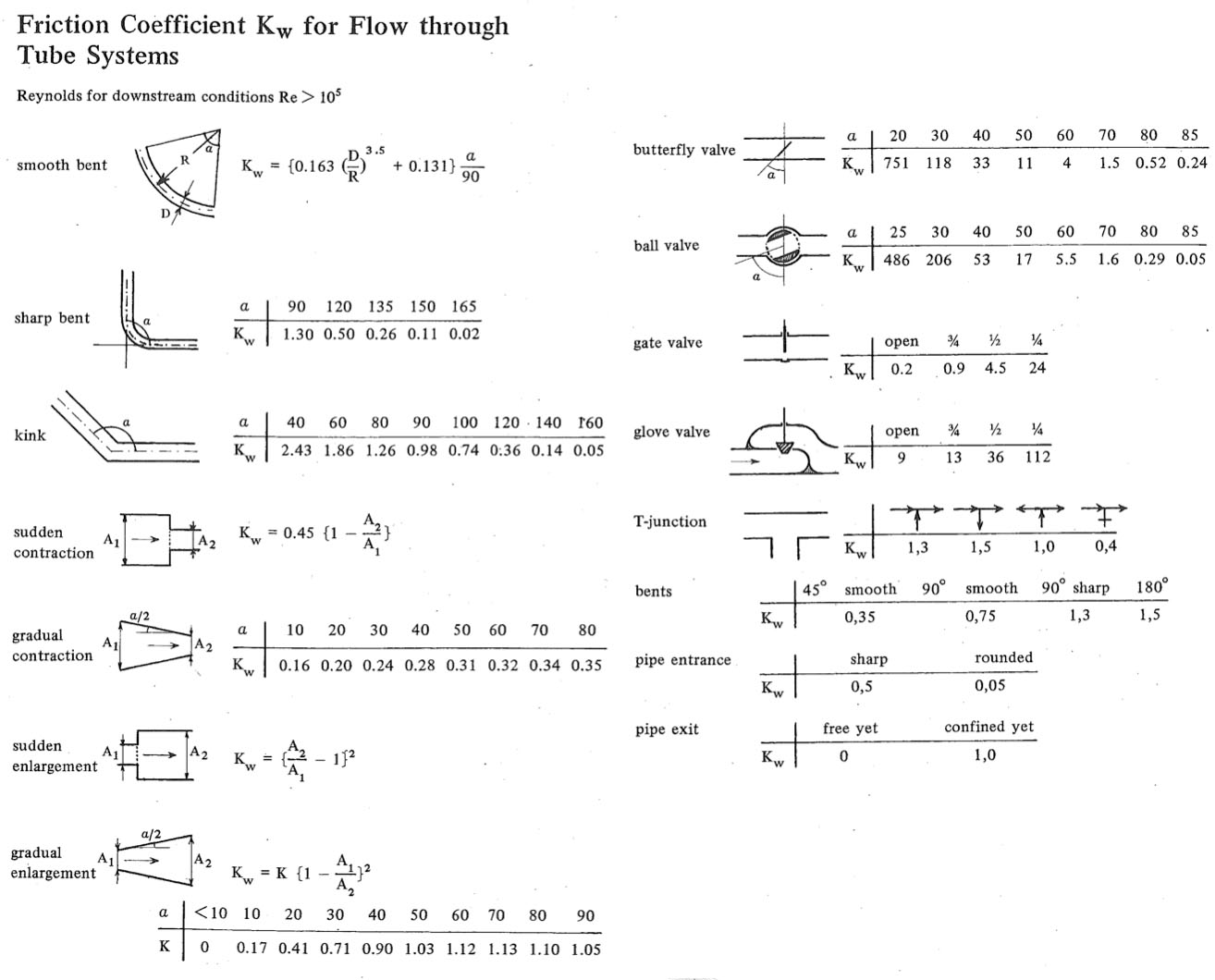
Fig. 24.9 Correlaties voor verschillende appendages. Let op dat altijd de stroomAFwaartse snelheid wordt genomen. Overgenomen uit de ``Transport Phenomena Data Companion’’ van Janssen en Warmoeskerken.

24.4. Opstelling en materialen

Voor het bestuderen van laminaire stroming zijn er twee basis opstellingen. De eerste is een open vat waaraan buisjes van verschillende lengte, diameter en appendages gemonteerd kunnen worden. Doordat het vat aan de bovenzijde open is, zal het debiet afhangen van het hoogte verschil. De tweede opstelling bestaat uit een gesloten vat met een extra inlaat. Als het vat leegloopt, neemt de druk bovenin het vat af waarna lucht via de extra inlaat wordt aangezogen. Dit principe zorgt ervoor dat de druk bovenin het vat constant blijft. Dit garandeert dan weer een constant debiet.