01 Super Balls, Double Ball Drop

Aim

Showing that when a superball of small mass resting on top of a superball of large mass is dropped from a low height, the small ball ideally rebounds to nearly nine times its original height.

Subjects

• 1E10 (Moving Reference Frames)

• 1N20 (Conservation of Linear Momentum)

Diagram

Fig. 32 .

Fig. 33 The Astro-superball

Equipment

• 1 superball of large mass (basketball).

• 1 superball of small mass (table-tennis ball).

• Astro-superball

Presentation

A superball of small mass is dropped and rebounds almost to its original height. Next, the small superball is held about \(10~\mathrm{cm}\) above a larger superball. This combination is dropped simultaneously, and after striking the floor, the small ball launches upward and can reach a height up to nine times the original dropping height.

Explanation

Just before striking the floor, both balls have a velocity \(v\) downward. Just after the combination hits the floor, the larger ball rebounds upward with a velocity \(v\), while the smaller ball is still moving downward with a velocity \(v\). This makes their relative speed \(2v\) — the small ball is approaching the large ball at \(2v\). If the collision between the balls is elastic, the smaller ball will rebound with a velocity of \(2v\) relative to the larger ball, but in the opposite direction. Since the larger ball is moving upward at \(v\), the small ball’s velocity relative to the floor becomes \(v + 2v = 3v\) upward.(See Figure 182)

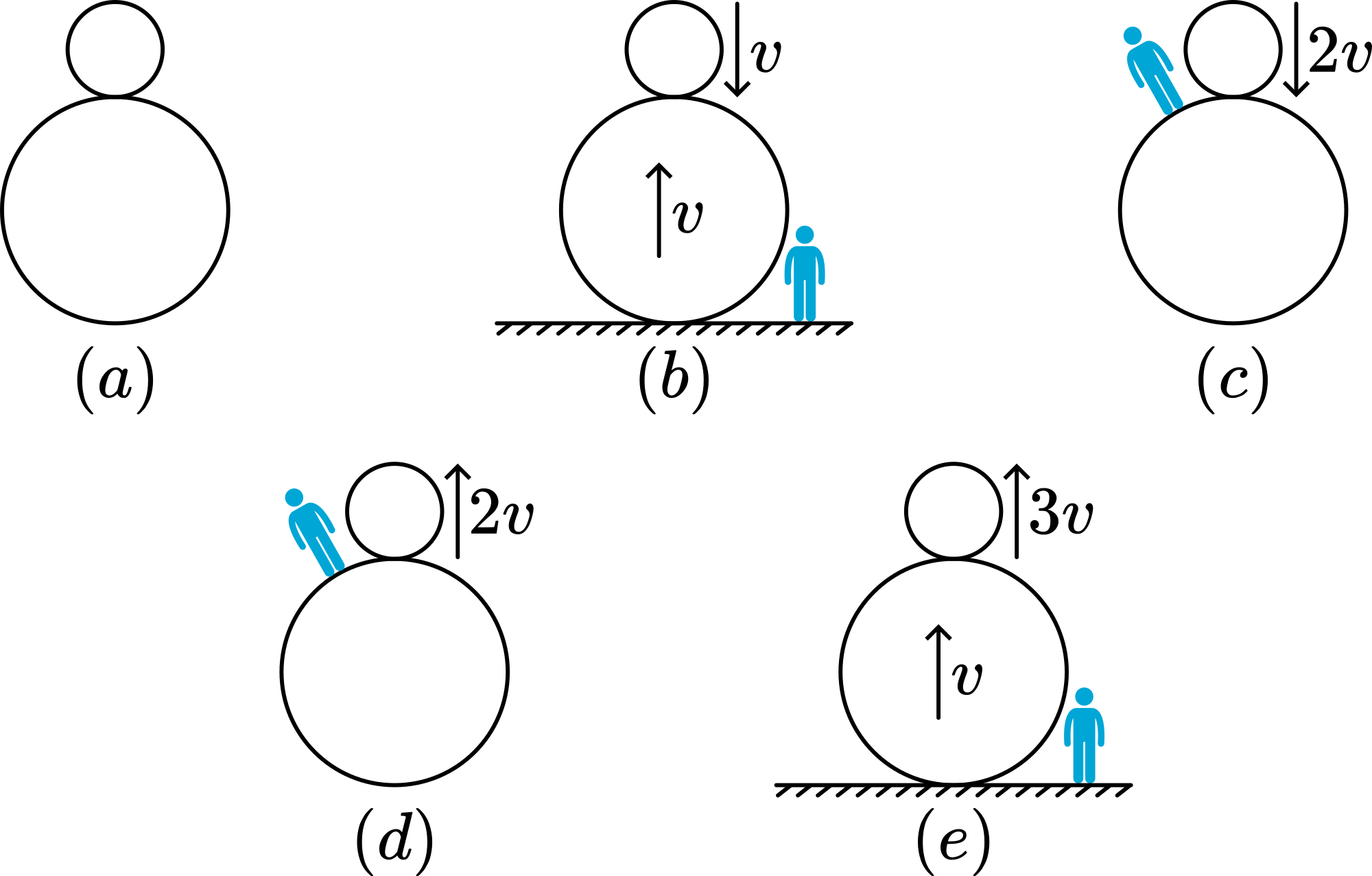
Fig. 34 .

The small ball would have gone up with a velocity \(v\) if it had just hit the floor, but now it takes off with a velocity \(3v\). Because \(m g h=1 / 2 m v^{2}\), a 3 times higher take-off velocity means that it goes 9 times higher.

Remarks

• Do not rest the table-tennis ball on the basketball and drop it in such a combination. When this is done, the table-tennis ball stays fixed to the basketball (aerodynamic reason), and for this demonstration, it is required that on hitting the ground, there is some distance between the two balls.

• It is recommended to practise the drop beforehand, especially to ensure that the small and large balls are released simultaneously.

• An extension of the demonstration is to drop a stack of three or even more balls (See Figure 181). When a three-ball combination is dropped, the top ball approaches a maximum of 49 times the initial release height. In order to drop the Astroball-stack perfectly vertical, wet your fingers holding the stack and slowly let it slip away.

• The experiment does not perform very well on a wooden floor.

Sources

• The Physics Teacher, vol. 21, no. 7, pag. 466, Superball problem, G. Stroink

• Ehrlich, Robert, Turning the World Inside Out and 174 Other Simple Physics Demonstrations, pag. 60

• Stark Verlag, Astro-Blaster 11938