04 Colliding Balls (1)#
Aim#
To demonstrate many combinations of elastic collisions. To test momentum conservation.
Subjects#
1N20 (Conservation of Linear Momentum)
Diagram#

Fig. 166 .#
Equipment#
Elastic balls hanging from a frame (“Newton’s cradle”)
Presentation#
The identical balls are bifilarly suspended in a straight row. In horizontal equilibrium the balls are just in contact. Speeds at the time of contact are, to a first approximation, proportional to the horizontal displacement from rest position.
Two balls are suspended. One ball is pulled out and released. It hits the other and this one bounces out to the other side; the first ball being at rest now. (See Figure 167.)
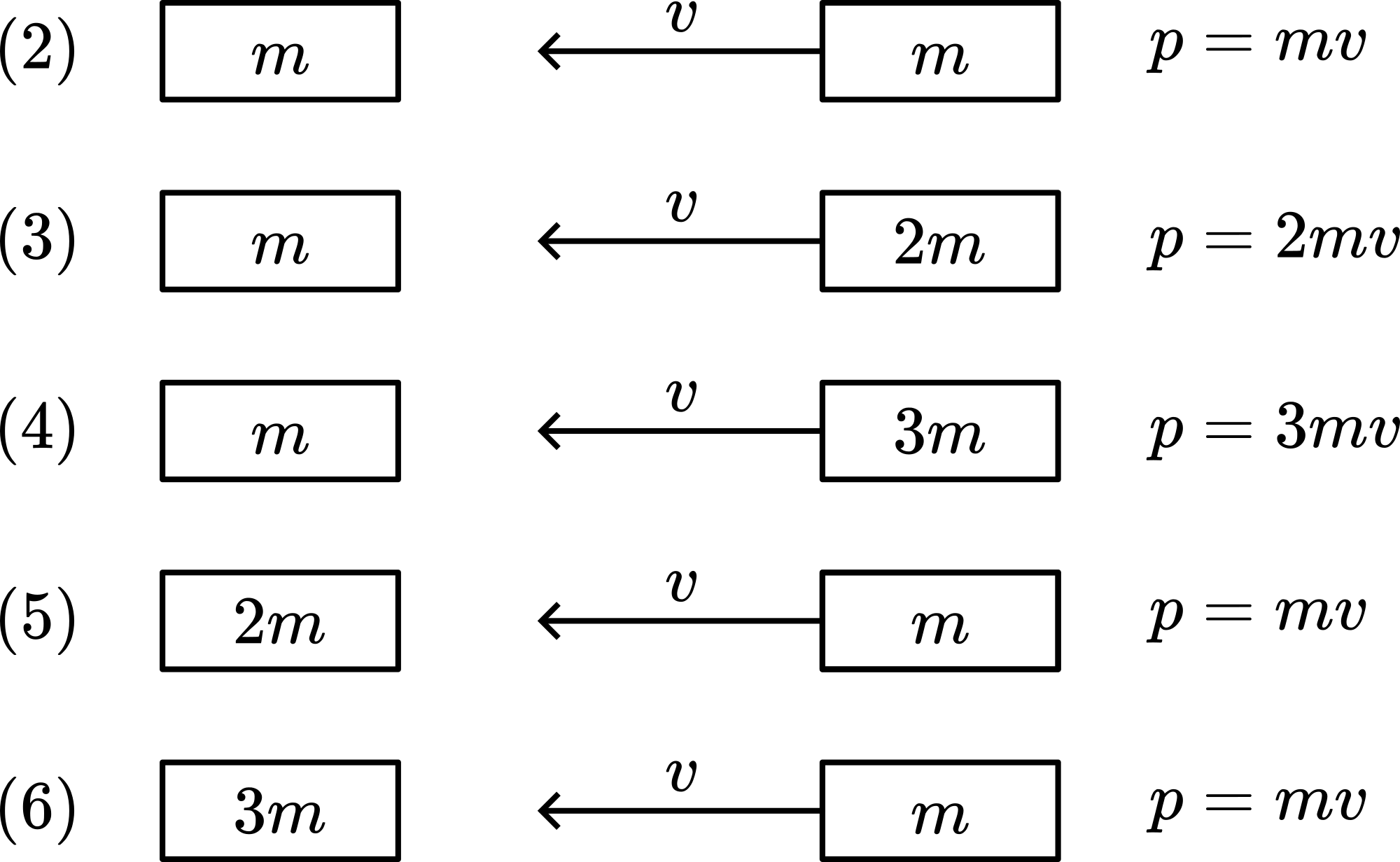
Fig. 167 .#
Both balls are pulled out and released. They hit and both rebounce almost to the original height. (See Figure 168.)
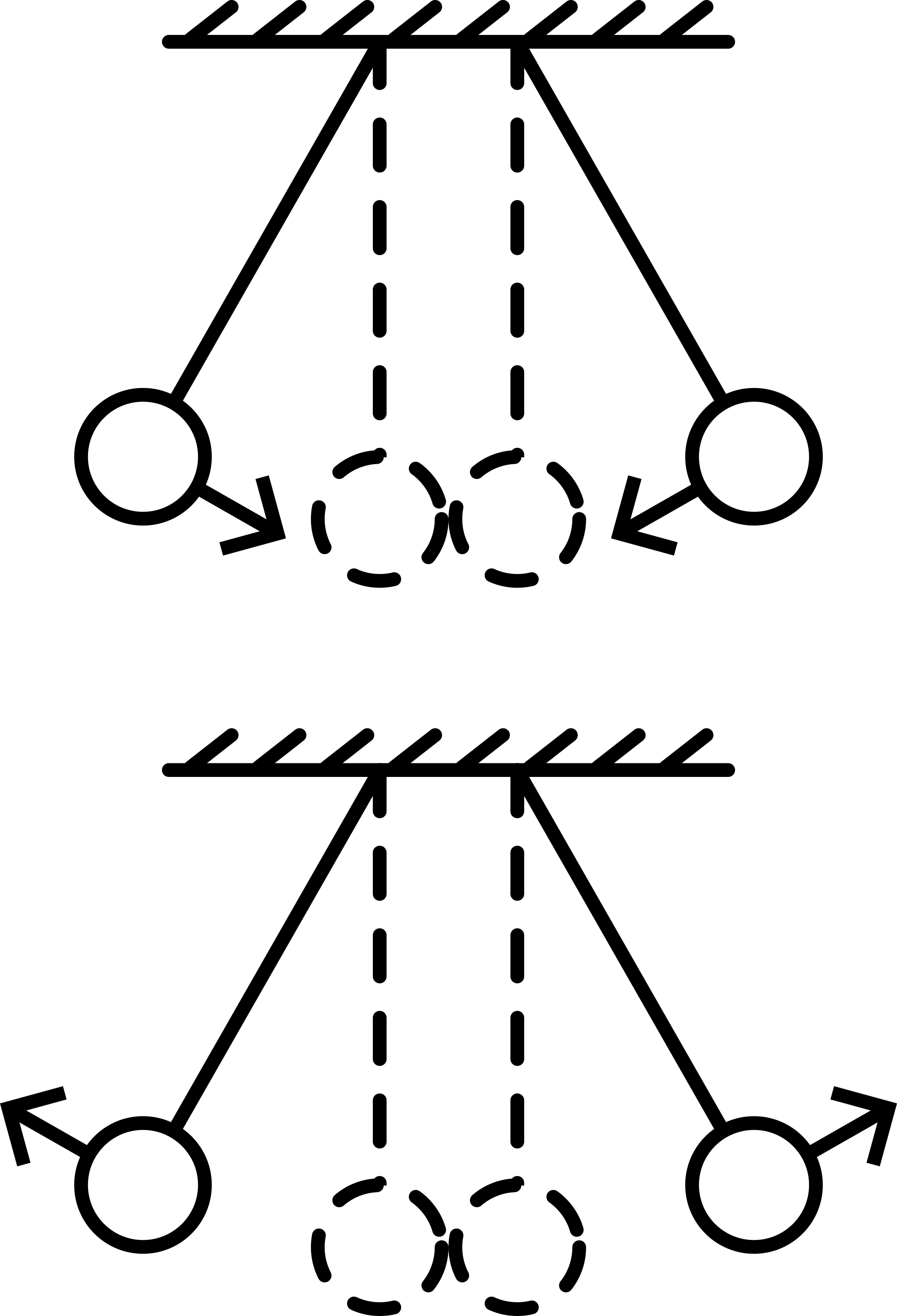
Fig. 168 .#
Both balls are pulled out but one ball more than the other. In this way the two balls will have different speeds. They are released, hit, and it can be observed that after the collision the two balls have interchanged their speeds. (See Figure 169.)
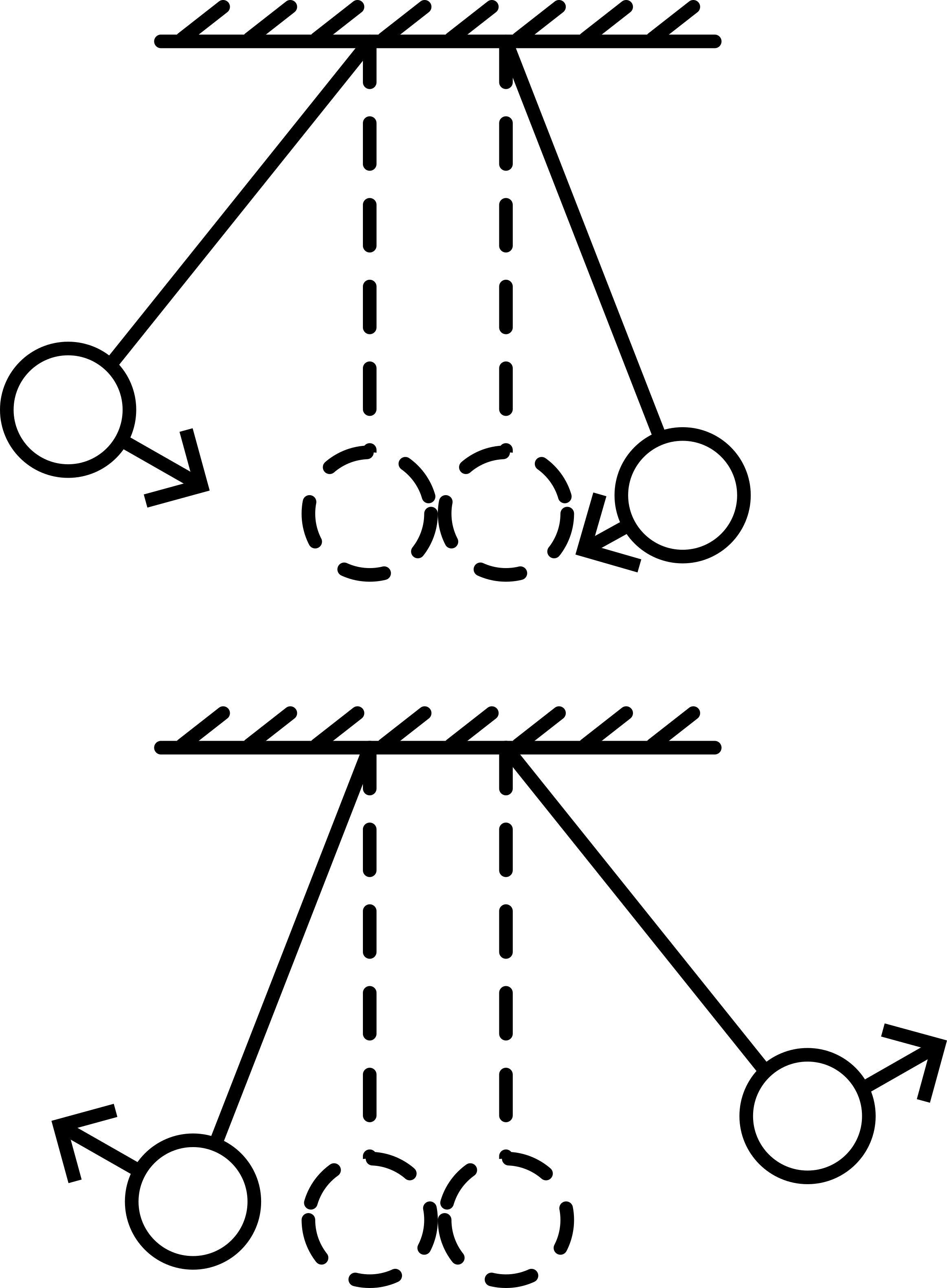
Fig. 169 .#
More balls are suspended.
When 3 (or 4 , or 5 , etc.) balls are suspended the demonstrations performed with two balls can be repeated. The observed phenomena are similar. The balls between the two outer balls are not taking part in the movements. (See Figure 170.)
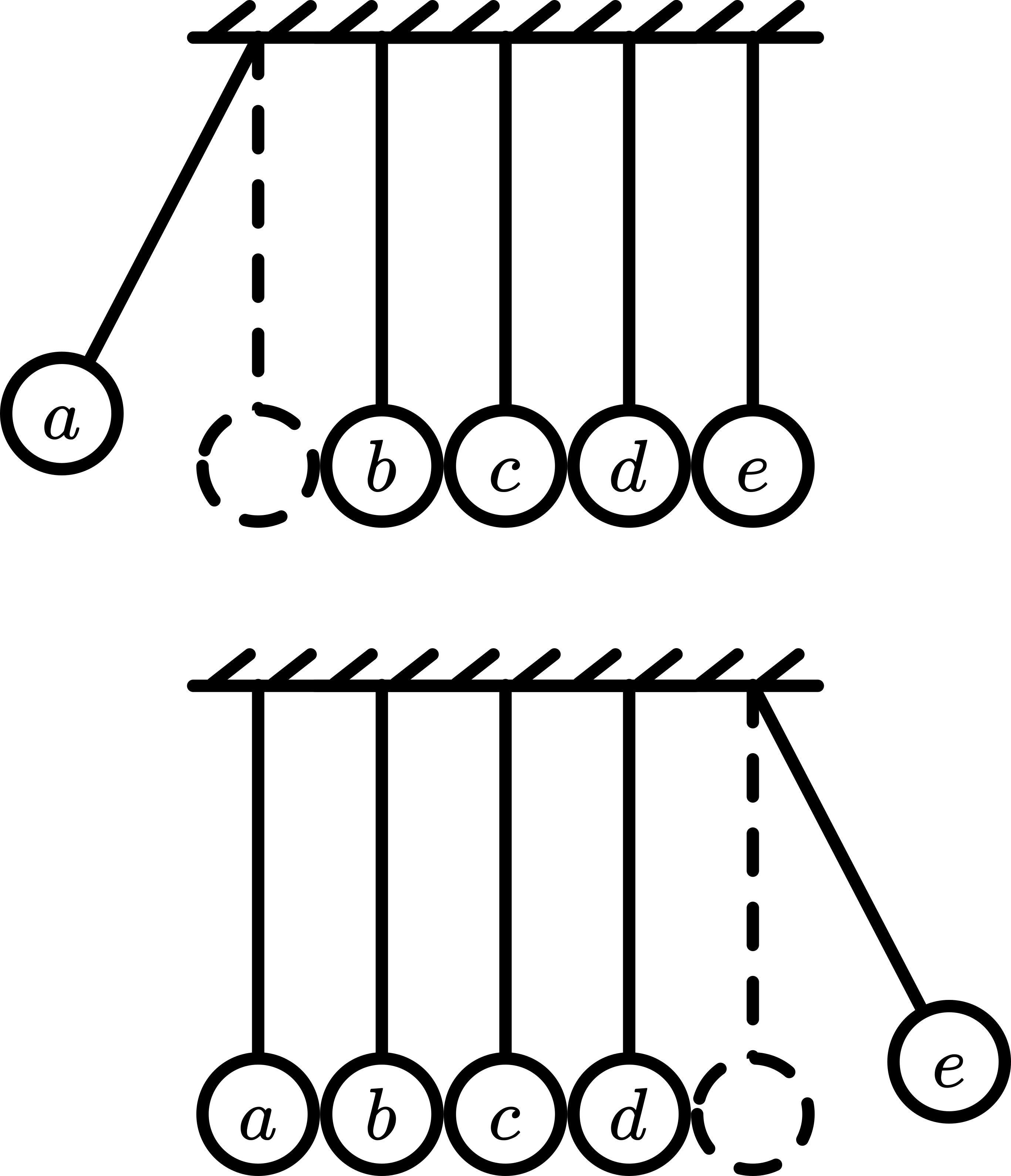
Fig. 170 .#
When two balls are pulled out and released, they hit the others and two balls bounce out to the other side. With three, three bounce out, etc. It is always the same number of balls. (See Figure 171.)
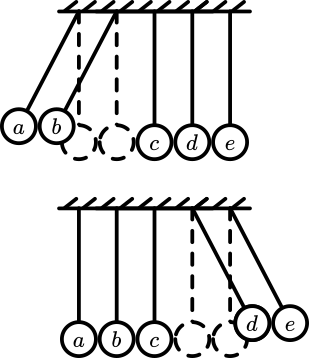
Fig. 171 .#
Two balls of different mass ( \(m\) and \(3 m\) ).
\(m\) is hanging in its rest position and \(3 m\) is pulled out and released. After the collision \(m\) is launched and \(3 m\) follows it but with reduced speed. After reversing their direction, they collide again in the middle and after this second collision \(m\) hangs at rest and \(3 m\) rebounces to its original height.
\(3 m\) is hanging in its rest position and \(m\) is pulled out and released. After the collision, \(3 m\) is launched and \(m\) rebounces but not to its starting position. Both masses have the same speed when they collide again exactly in the rest position and after this second collision \(3 m\) is at rest and \(m\) rebounces to its starting position.
Both balls are pulled out and released at the same height, so they have the same speed. After the collision, \(3 m\) is at rest and \(m\) bounces to a much higher height. \(m\) reverses its direction and there is a second collision. Now both balls rebounce to their original height.
In all three demonstrations the starting position returns after two collisions.
Explanation#
Figure 172 shows the situation before and after an elastic collision. In an elastic collision, both momentum and kinetic energy are conserved. This means that \(v_{\text {rel }}\) will not change: \(u_{2}-u_{1}=V_{\text {rel }}\)
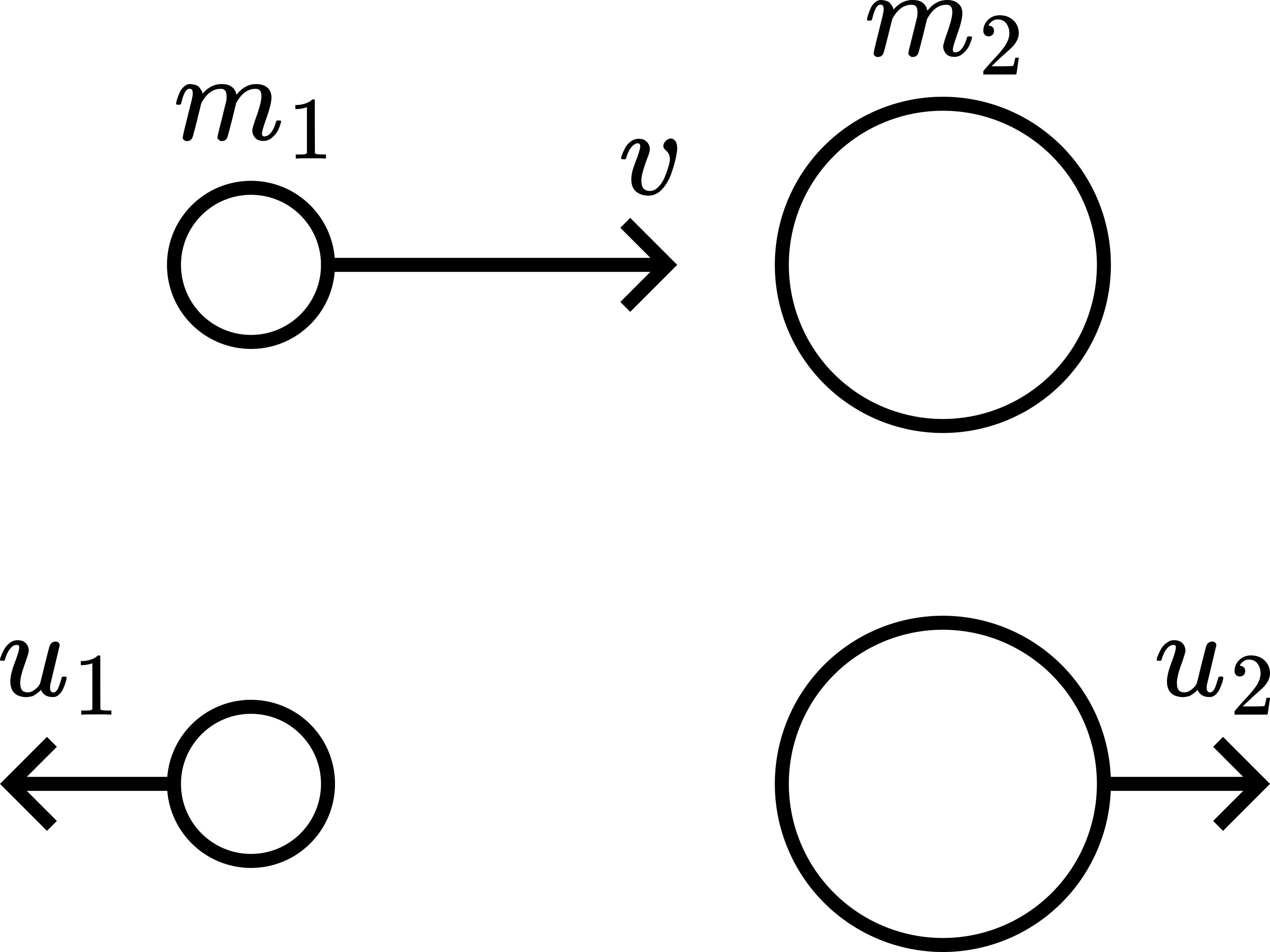
Fig. 172 .#
Momentum is conserved:
These two equations give us:
and
The next table shows the results of different situations concerning our demonstrations.
\(m_{1} / m_{2}\) |
\(\mathrm{u}_{1}\) |
\(\mathrm{u}_{2}\) |
|---|---|---|
\(1 / 3\) |
\(-1 / 2 v\) |
\(\underline{1 / 2 v}\) |
1 |
0 |
\(\underline{v}\) |
3 |
\(1 / 2 \quad v\) |
\(\underline{3 / 2 v}\) |
This table explains the behavior shown in presentation 1 and 3 .
In the demonstration of Figure 170, \(a\) hits \(b\). \(b\) gets the speed of \(a\) (see table) and immediately hits \(c\). \(b\) comes to rest and \(c\) gets the speed of \(b\) and immediately hits \(d\) etc. At the end, \(e\) is launched with the speed \(v\) that \(a\) originally had.
In the demonstration of Figure 171 , the first thing that happens is that \(b\) hits \(c\). \(b\) comes to rest and finally \(e\) is launched. In the meantime \(a\) hits \(b\) and \(a\) comes to rest and finally \(d\) is launched.
If not reasoning step by step, the question could be raised why ball \(e\) is not coming out with double velocity. After all this would conserve momentum. But checking kinetic energy will show that in that case kinetic energy is not conserved.
Remarks#
In succession to demonstration 2 (in the end with three balls), one ball with mass \(3 \mathrm{~m}\) and speed \(v\) hits the row of balls at rest. It can be seen that in this case not the last three balls are launched with speed \(v\), but that all balls are moving now with different speeds and also the \(3 m\)-ball is still moving.
Sources#
Jewett Jr., John W., Physics Begins With an M… Mysteries, Magic, and Myth, pag. 74, 83
Sutton, Richard Manliffe, Demonstration experiments in Physics, pag. 56
Roest, R., Inleiding Mechanica, pag. 118-119
Borghouts, A.N., Inleiding in de Mechanica, pag. 103-104
Ehrlich, Robert, Turning the World Inside Out and 174 Other Simple Physics Demonstrations, pag. 58
Leybold-Heraeus, Physikalische Handblätter, pag. DK 531.662; a
