04 Explosion

Aim

To demonstrate that in an explosion, the centre of mass does not move.

Subjects

• 1D40 (Motion of the Centre of Mass)

• 1N20 (Conservation of Linear Momentum)

Diagram

Fig. 16 .

Fig. 17 .

Equipment

• Dynamics cart.

• Masses.

• Collision cart.

• Cart-track, \(2.2 \mathrm{~m}\), with end-stops (with magnets).

• Small table.

• Mass balance (scale).

• Short stick.

• Air level.

Safety

• An assistant should be present to (potentially) catch the track.

Presentation

Preparation

Place the two supports of the cart track in the middle of the track, about \(4 \mathrm{~cm}\) apart, to balance the track on the small table (see Figure {number}). Use an air level to carefully balance the small table horizontally, then do the same for the track.

Presentation

The dynamic cart and the collision cart are put on the scale to show that their masses are equal. Now the plunger of the dynamic cart is pushed completely inward and latched.

1. Carefully position the dynamic cart and collision cart against each other on the balanced track. Give the plunger release button a short blow with the stick and watch the two carts move to the ends of the track. The cart-track with the moving carts remains balanced (even when the carts bounce at the end stops!)

2. Now, a mass equal to the mass of one cart is put on top of one of the carts (see Remarks to know where the \(CM\) is). The demonstration is repeated: The heavier cart is moving slower, but the track with the moving carts remains balanced!

3. The demonstration can be performed a third time with two masses put on top of one cart, making the mass-ratio between the two carts equal to \(3: 1\).

4. As an extra, in the second and third demonstrations, with the carts of different masses, you need to catch the track when one of the carts bumps against the end-stop, as the track will not remain balanced. Present this to the students as a challenge: “The set-up becomes unbalanced when one of the carts bumps into the end-stop, so the centre of mass moves away from the point of support!”

• Question: “What makes the centre of mass move away?”

• Answer: “An external force.”

• Question: “What and where is this external force?”

Explanation

1. 2. and 3.

The centre of mass (\(CM\)) of a fixed number of particles is defined as the average position ( \(R_{C M}\) ) of those particles:

\[R_{c m}=\frac{m_{1} x_{1}+m_{2} x_{2}}{m_{1}+m_{2}}\]

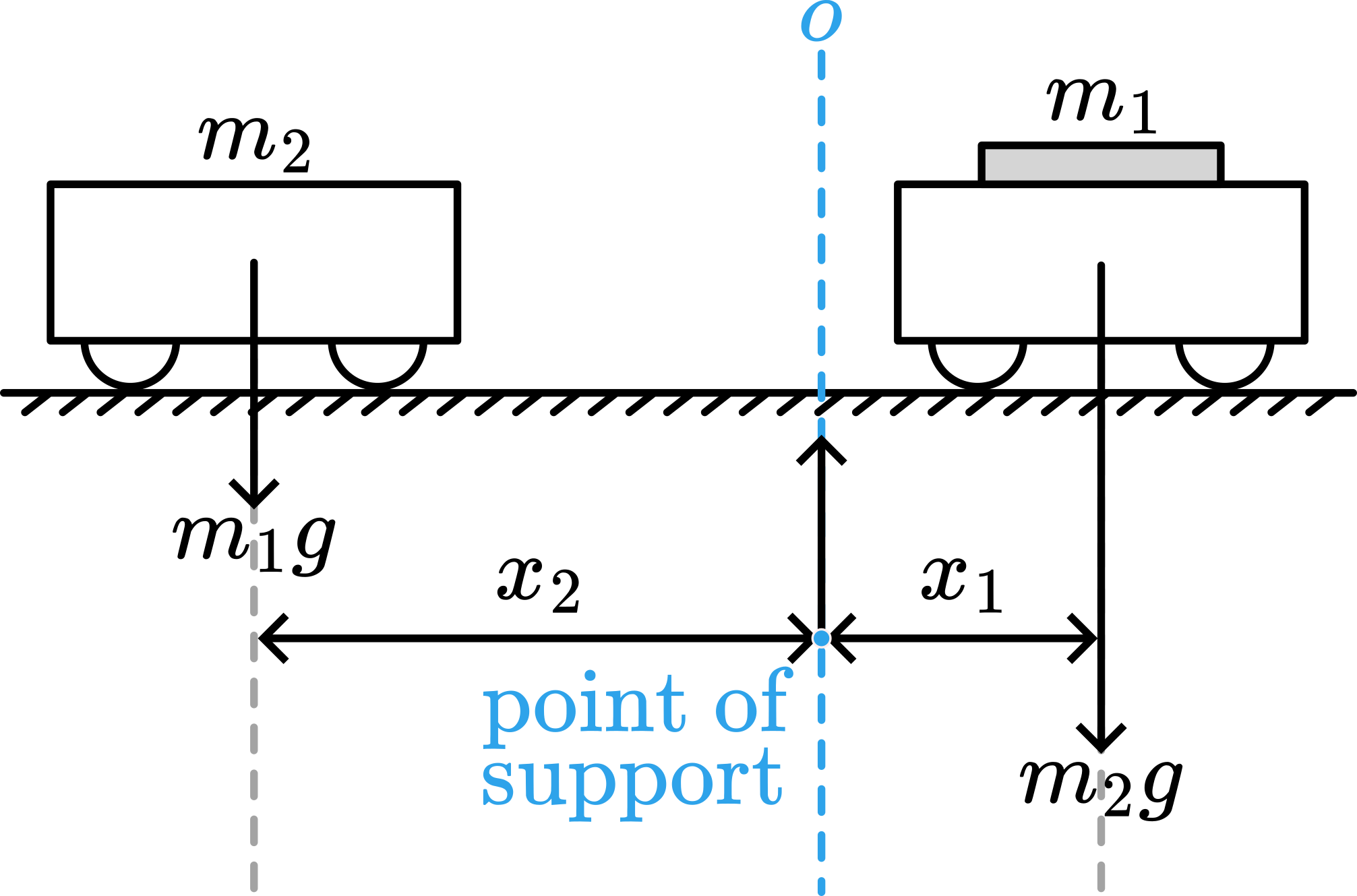
Fig. 18 .

At the start of the demonstration (before the explosion) \(R_{c m}=\frac{m_{1} 0+m_{2} 0}{m_{1}+m_{2}}=0\) (Point of support being the zero-reference.)
After the explosion of the two carts \(m_{1} v_{1}+m_{2} v_{2}=0\) (conservation of momentum).
Since \(x=v t; m_{1} x_{1}+m_{2} x_{2}=0\), so \(R_{CM}=0\) and \(CM\) remains at the zero-coordinate; the track remains balanced.

Extra.

When one cart hits the end stop ( \(m_{2}\) in Figure 19), there is at that location a change of momentum \(\Delta p=2 m v\) of the cart. The track experiences an impulse of \(\left|\int_{0}^{\Delta t} F d t\right|=2 m v\). There is no external impulse imparted to the track, so this impulse must be balanced somewhere. Friction force at the support takes care for that \(\left|\int_{0}^{\Delta t} F_{f} d t\right|\). And also: \(F_{f}=-F\) (Newton 3).

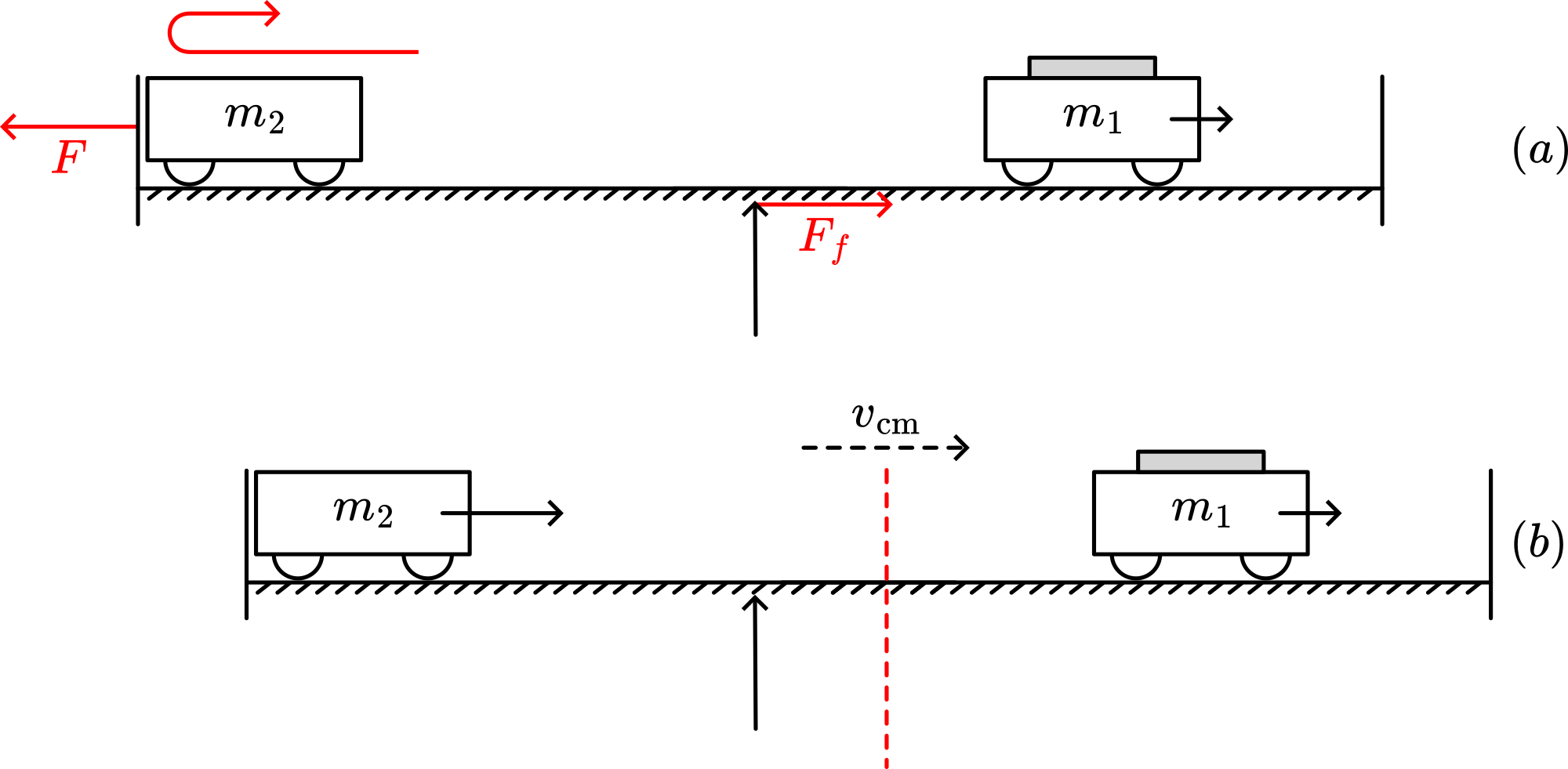
Fig. 19 .

In Figure 19A this \(F_{f}\) gives the whole assembly a velocity to the right, displacing \(CM\) to the right. \(CM\) will keep on moving to the right (Newton 1), increasing the unbalance more and more.

Remarks

• When carts of different masses are placed on the balanced track, take care that their common centre of mass is placed right above the balanced point of the track (see Figure 20). When \(m_{1}=2 m_{2}\), then \(y=1 / 61\); when \(m_{1}=3 m_{2}\), then \(y=1 / 41\).

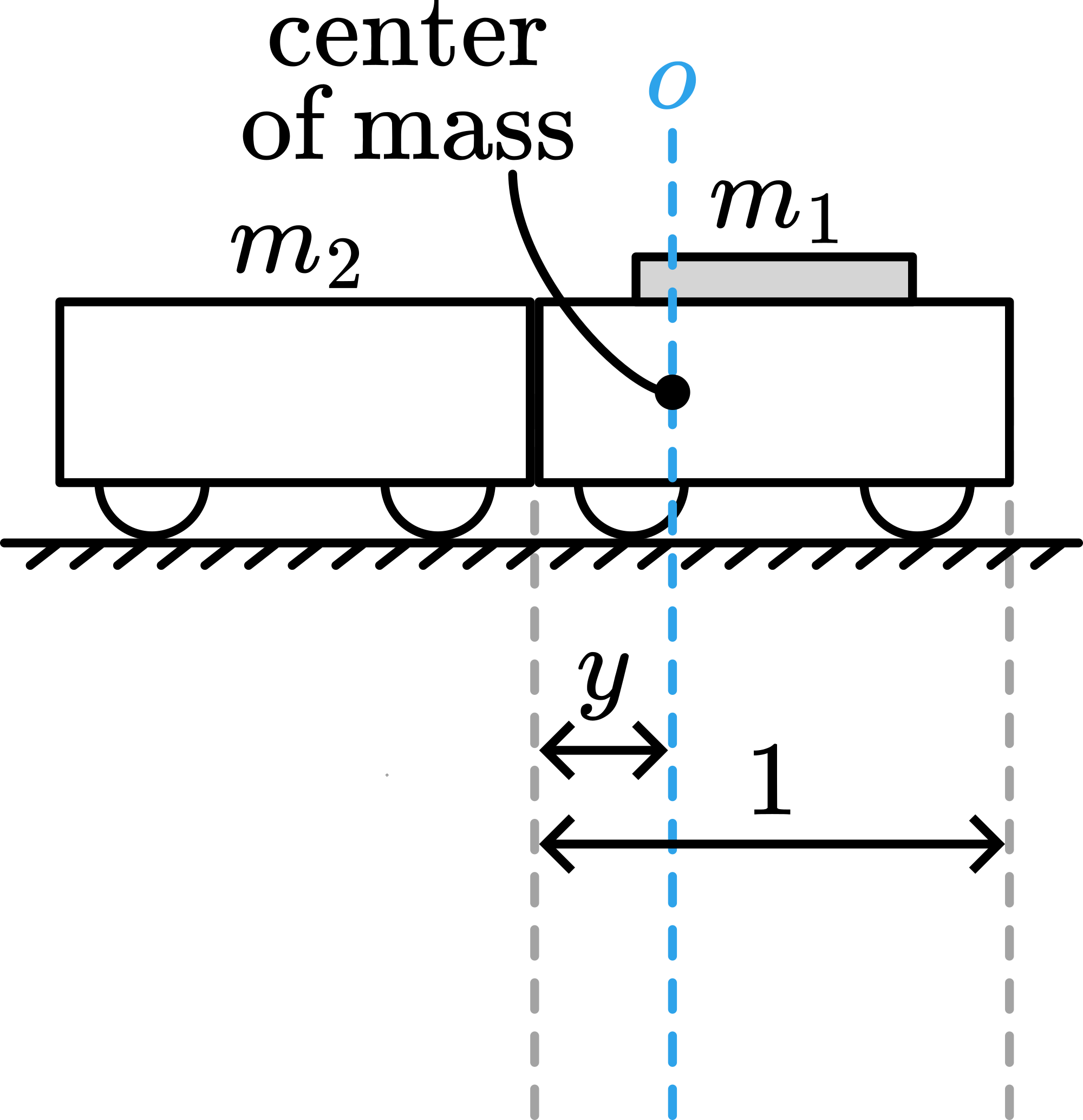
Fig. 20 .

Sources

• PASCO scientific, Instruction Manual and Experiment Guide for the PASCO scientific Model ME-9458 and ME-9452, experiment 1 and 11

• Mansfield, M and O’Sullivan, C., Understanding physics, pag. 124-129