04 Soap Film#
Aim#
To show the interference in a thin soap film.
Subjects#
6D30 (Thin Films)
Diagram#

Fig. 633 .#
Equipment#
Wineglass with a small hole cut in its cup, and a collar of black paper around its stem (see Diagram C).
Lamp, 12V/90W
Condenser lens, \(f=50 \mathrm{~mm}\).
Imaging lens, \(f=300 \mathrm{~mm}\).
Short optical rail.
Round screen of black paper, to screen straight transmitted light (see Diagram C).
Petri dish with a soap solution
Presentation#
Having set up the demonstration as shown in Diagram, an image of the rim of the wineglass is projected on the wall. Using a felt pen you mark the position of the wineglass on the table. Using your finger you can show that the projected image is upside down. Dip the wineglass in the soap solution, so that the rim of the glass has a film on it. Put the glass back in its marked position.
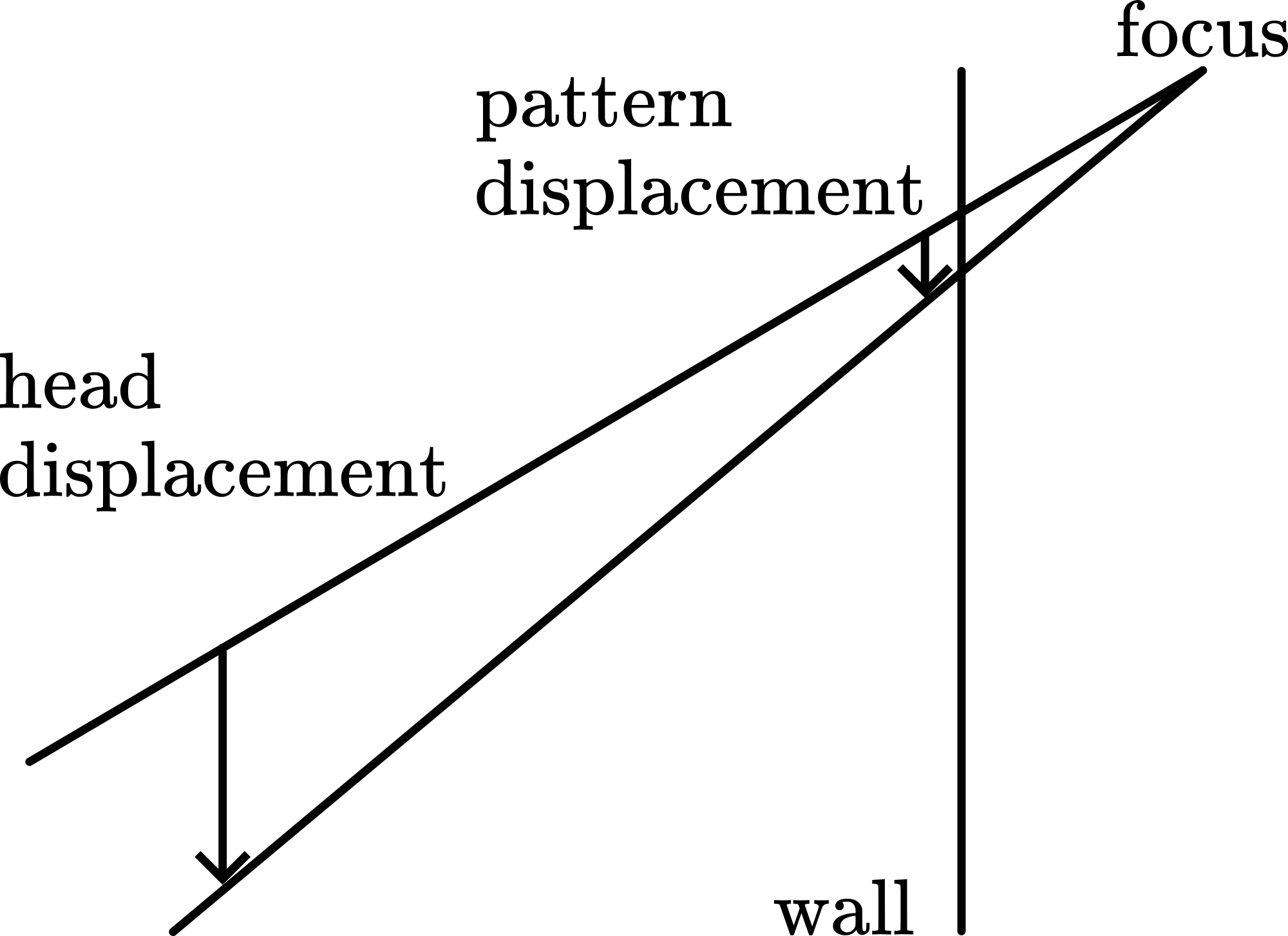
Fig. 634 .#
First, the image is whitish, but very soon a reddish haze appears, transforming into red and white stripes. Gradually more colors appear (see Figure 634A) and when full color rainbows appear, also black stripes show themselves. Finally a broad whitish band appears on the upper side, abruptly followed by complete darkness (see Figure 634B). Then the film breaks.
The demonstration is repeated a couple of times because the color transformations go pretty fast. Sometimes it needs to be repeated because the soap film breaks too soon.
Explanation#
The soap film is a water sandwich. A layer of water is held between two layers of soap molecules. When the soap film is vertical the water drains down under the pull of gravity so that the top of the film becomes thin while the bottom becomes thick. Light reflects from the front and from the back of the soap film. These two reflections add up producing interference of light. Some wavelengths (colors) add up out of phase and are canceled while other colors add up in phase and are strengthened. Different thicknesses of soap film cancel/strengthen different colors.
Black region#
The light waves reflected from the front of the soap film are inverted (phase shift \(\pi\) ), while those from the back are not. Thus, soap films that are thin compared to all wavelength of light reflect no light at all.
White region#
Going down the film until it is \(1 / 4\) wavelength of blue light in thickness the blue light is reflected strongly. At this point the film is about \(1 / 8\) of a wavelength of red light thick (taking that the wavelength of red light is about twice that of blue). So some red light is reflected. The result is that the transparent film shows a metallic white sheen that grows bluer and bluer towards the black region.
Regions of thicker films#
When the film is \(1 / 2\) of a wavelength of blue light thick the blue waves cancel. But now the film is also \(1 / 4\) of the wavelength of red light thick, and the red light is reflected strongly. Every integral multiple of \(1 / 2\) blue wavelength, blue light is removed, every odd multiple of \(1 / 4\) wavelength of blue light is strengthened.
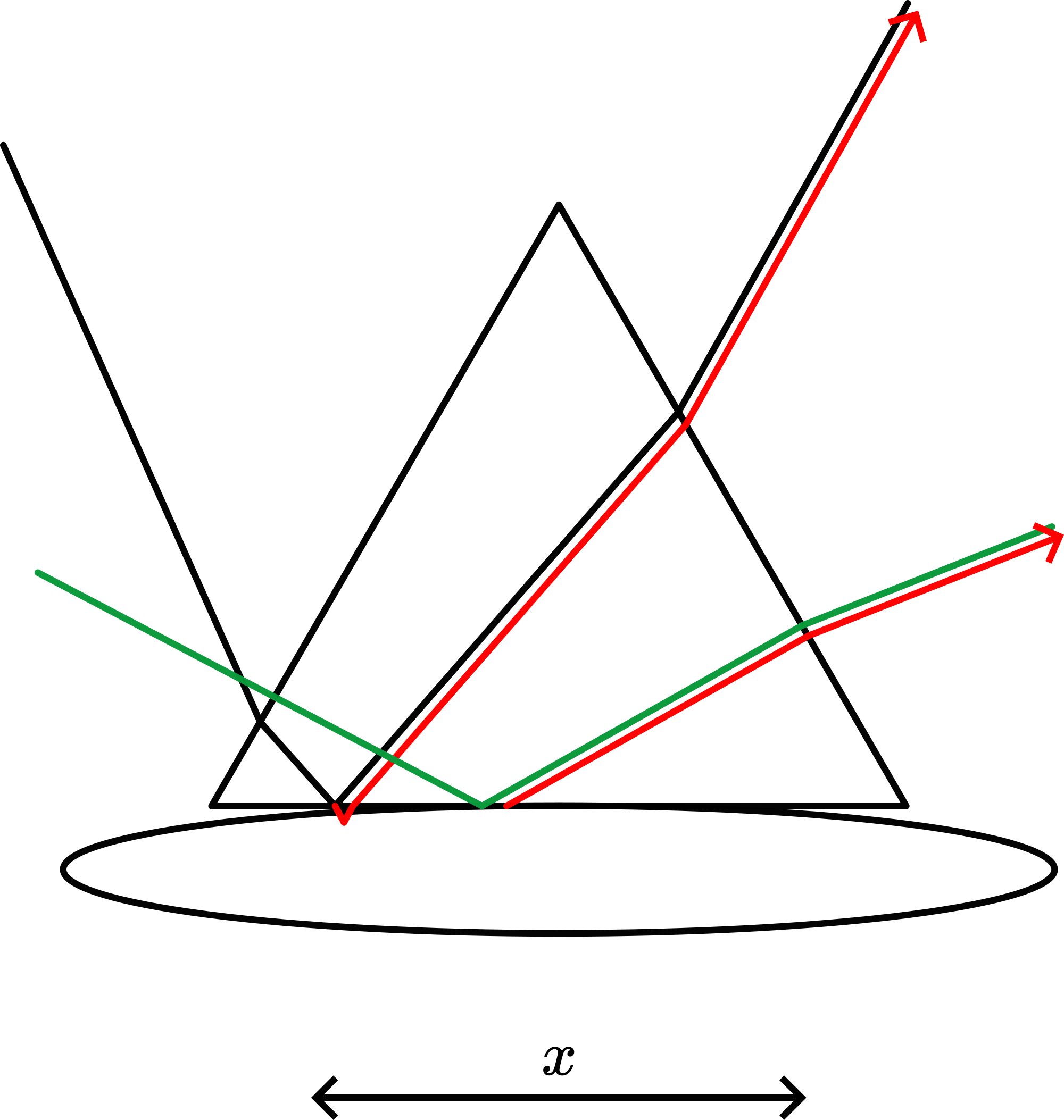
Fig. 635 .#
The same holds for red light. Figure 635 shows the result of this simplified blue-red dance. This figure clarifies that red dominates blue: the maximum of blue has always some red in it, while the maximum of red is “pure” red. In incandescent lamplight this is even stronger, due to the fact that red has a higher intensity in that light than blue.
Remarks#
The color pattern can also be easily observed in normal daylight. But for a larger group projection will be necessary.
The wineglass has a small hole cut in its cup. When you use an ordinary wineglass you will notice that the soap film will bend inward. Colors can still be observed, but projecting a sharp image is not possible.
Robert Hooke first reported observing the transparent film in a letter to the Royal Society. His letter indicates that he thought that the film actually did not exist where it was transparent. A simple experiment of poking the invisible film and so breaking it proves the existence of the invisible film.
See also the demonstration “Oil film”.
Sources#
Biezeveld, H. and Mathot, L., Scoop, Natuurkunde voor de bovenbouw, part 4/5 vwo, pag. 128-129
Giancoli, D.G., Physics for scientists and engineers with modern physics, pag. 877-879 and 880
Hecht, Eugene, Optics, pag. 398
PSSC, College Physics, pag. 137-141
