01 Elastic Collisions

01 Elastic Collisions#

Aim#

To explore the conservation of momentum in elastic collisions.

Subjects#

  • 1N20 (Conservation of Linear Momentum)

Diagram#

../../../../../_images/figure_068.png

Fig. 157 .#

Equipment#

  • Two collision carts with magnetic bumpers on both ends.

  • Masses for carts.

  • Cart track, \(2.2\mathrm{~m}\), with end-stops.

  • Mass balance.

Presentation#

The cart track is carefully leveled (by setting a cart on the track to see which way it rolls).

  • One cart is placed in the middle of the track. Give the other cart an initial speed towards the cart at rest. Observe that after the collision the second cart moves with the speed of the first and that the first cart stops. When the second cart rebounds elastically at the end-stop this phenomenon repeats.

  • Both carts are given a certain speed towards the middle of the track; Equal speeds: Then after collision they recede with equal speeds. Different speeds: Then after collision they have interchanged their speeds.

  • By means of the extra masses, one of the carts (mass \(=m\) ) is given a mass of \(2 m\) or \(3 m\). Now the next demonstrations can be performed:

    (Let students predict what will happen before showing the concerned demonstration.)

    1. The \(2 m\)-cart stands at rest in the middle of the track. The \(1 m\)-cart approaches at a certain speed. Observe that after the collision the \(1 m\)-cart reverses its direction of movement and is slowed down and that the \(2 m\)-cart is launched and has a higher speed then the \(1 m\)-cart after the collision (actually the \(\mathbf{2 m}\)-cart is two times as fast as the Im-cart).
      as can be observed rather convincingly.

    2. The \(3 m\)-cart stands at rest in the middle of the track. The \(1 m\)-cart approaches at a certain speed. Observe that after the collision, the \(1 m\)-cart reverses its direction of movement and is slowed down and that the \(3 m\)-cart is launched. It can also be observed that both carts have the same speed.

    3. The \(1 m\)-cart stands at rest at one third of the track. The \(2 m\)-cart approaches at a certain speed. Observe that after the collision the \(2 m\)-cart continues moving in the same direction but is slowed down substantially and that the \(1 m\)-cart is launched with very high speed (actually, after the collision the \(\mathbf{1 m}\)-cart is \(\mathbf{4}\) times as fast as the \(2 m\)-cart).

    4. a. The \(\mathbf{1 m}\)-cart stands at rest at one third of the track. The \(3 m\) cart approaches at a certain speed. Observe that after the collision the \(3 m\)-cart continues moving in the same direction but is slowed down and that the \(\mathbf{1} \boldsymbol{m}\)-cart is launched with a very high speed. (The difference in speed between the two carts is less than in situation 3.)

      b. A nice extra demonstration is the following:
      Place the \(1 m\)-cart close to the end of the track. The \(3 m\)-cart approaches at a certain speed (not so high). After the collision, the \(1 m\)-cart bounces four times between the end-stops of the track and the still moving \(3 m\)-cart, but after that sequence the \(1 m\)-cart stands still and the \(3 m\)-cart moves with the same speed (opposite direction) it had before the collision.

Explanation#

In explaining the situations demonstrated, a rule introduced by Huygens can be used: “If in an elastic collision the sum of the impulses equals zero, then both objects reverse and have the same speed after the collision as before the collision.” (CM coordinate system.)

../../../../../_images/figure_152.png

Fig. 158 .#

This rule can easily be verified in applying conservation of momentum and conservation of kinetic energy. This method is shown here for situation 1 only, for the other situations the result is shown (see Figure 158 and Figure 159). Figure 159 shows the observed \(-v_{1}\) and \(v_{2}\) after the collision.

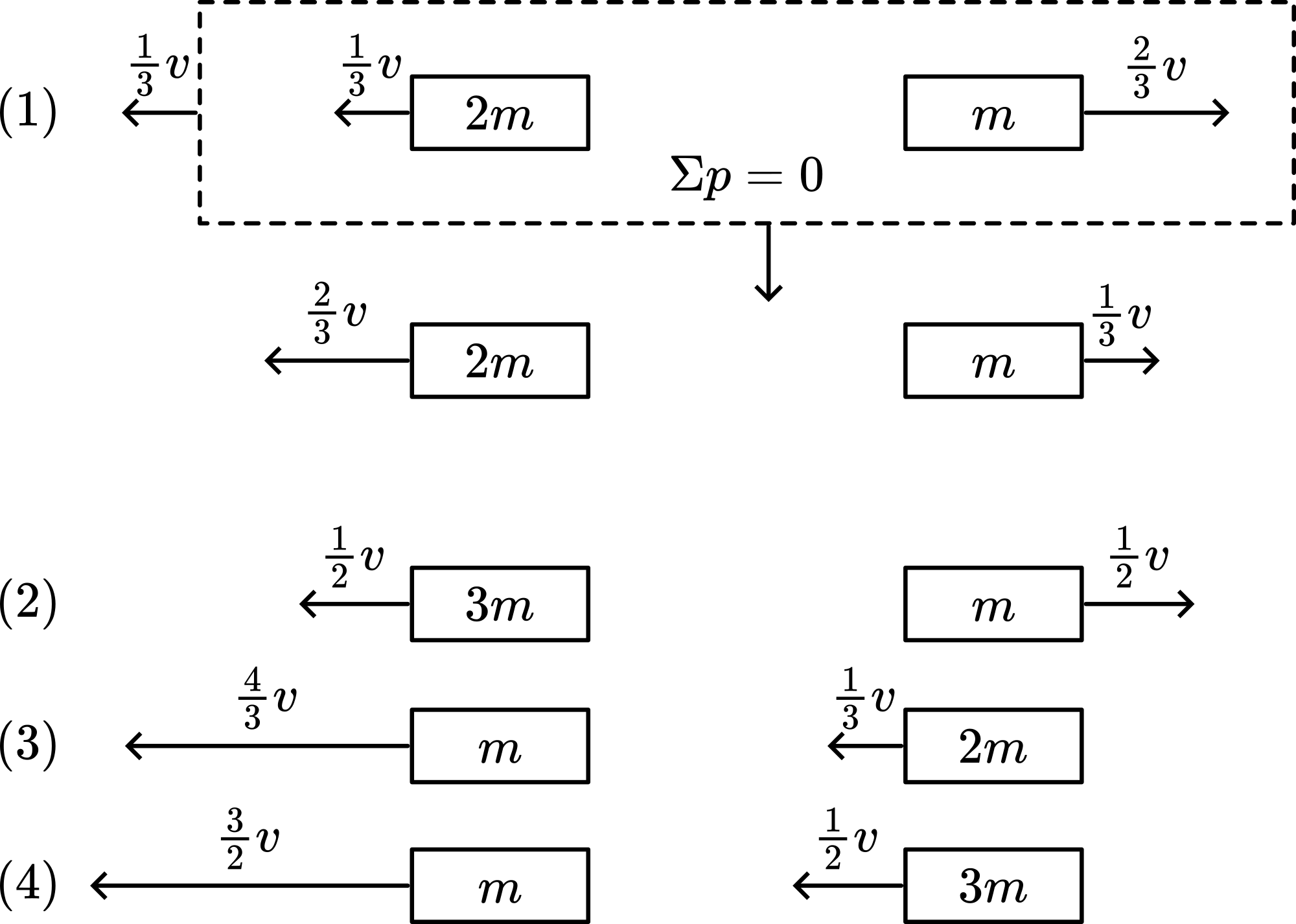
../../../../../_images/figure_222.png

Fig. 159 .#

Remarks#

  • Run each demonstration a couple of times to get agreement with your students on the observations.

  • The cart launched by hand should not be given too much speed, otherwise both carts touch each other and the collision is not completely elastic anymore. The carts might even derail.

  • \(\quad v_{2}{ }^{'}=v_{1}\left(\frac{2 m_{1}}{m_{1}+m_{2}}\right)\) means that when \(m_{2} \ll m_{1}\) then \(v_{2}{ }^{'} \approx 2 v_{1}\). In our demonstration sequence we approach \(v_{2}\) ‘up to \(1.5 v_{1}\)

Sources#

  • Biezeveld, H. and Mathot, L., Scoop, Natuurkunde voor de bovenbouw, part 4/5 vwo, pag. 148.

  • Mansfield, M and O’Sullivan, C., Understanding physics, 1998, pag. 126-128 and 135-136.

  • Giancoli, D.G., Physics for scientists and engineers with modern physics, third edition, pag. 212-217.

Contents