04 Sweet Spot#
Aim#
To show where a batter needs to hit a ball in order to transfer maximum energy to it.
Subjects#
1M40 (Conservation of Energy) 1Q40 (Conservation of Angular Momentum)
Diagram#

Fig. 214 .#
Equipment#
\(2.2 \mathrm{~m}\) track (PASCO-ME9452) with end stop.
Plunger cart (PASCO-ME9430), \(m=.51 \mathrm{~kg}\). The plunger is connected to a compression spring (see Figure 216)
Meterstick, pertinax, \(m=.42 \mathrm{~kg}\).
Meterstick, aluminum, \(m=1.64 \mathrm{~kg}\).
Clamping material to fix metersticks as pendulums and to limit its initial amplitude (see detail in Figure 215).
4 wooden markers, triangular shaped.
Presentation#
In the demonstration Percussionpoint it is shown to the students that a ball hitting a baseball bat will cause no impulse to your hands when you hold the bat at the percussion point. While presenting this demonstration, students often ask if this situation is also the “best” point for hitting the ball, meaning: where do we need to hit the ball to transfer maximum kinetic energy to it. Demonstration will show that this so-called “sweet spot” is not the same as the one related to the percussion point. Set up the demonstration as shown in the Diagram. The meterstick-pendulum has a limited amplitude thanks to a little bar functioning as a stop (see Figure 215). Clamp A and B shown in this figure can be used to shift the complete pendulum-system up and down. This makes it possible to choose where the meterstick-pendulum will hit the plunger cart.
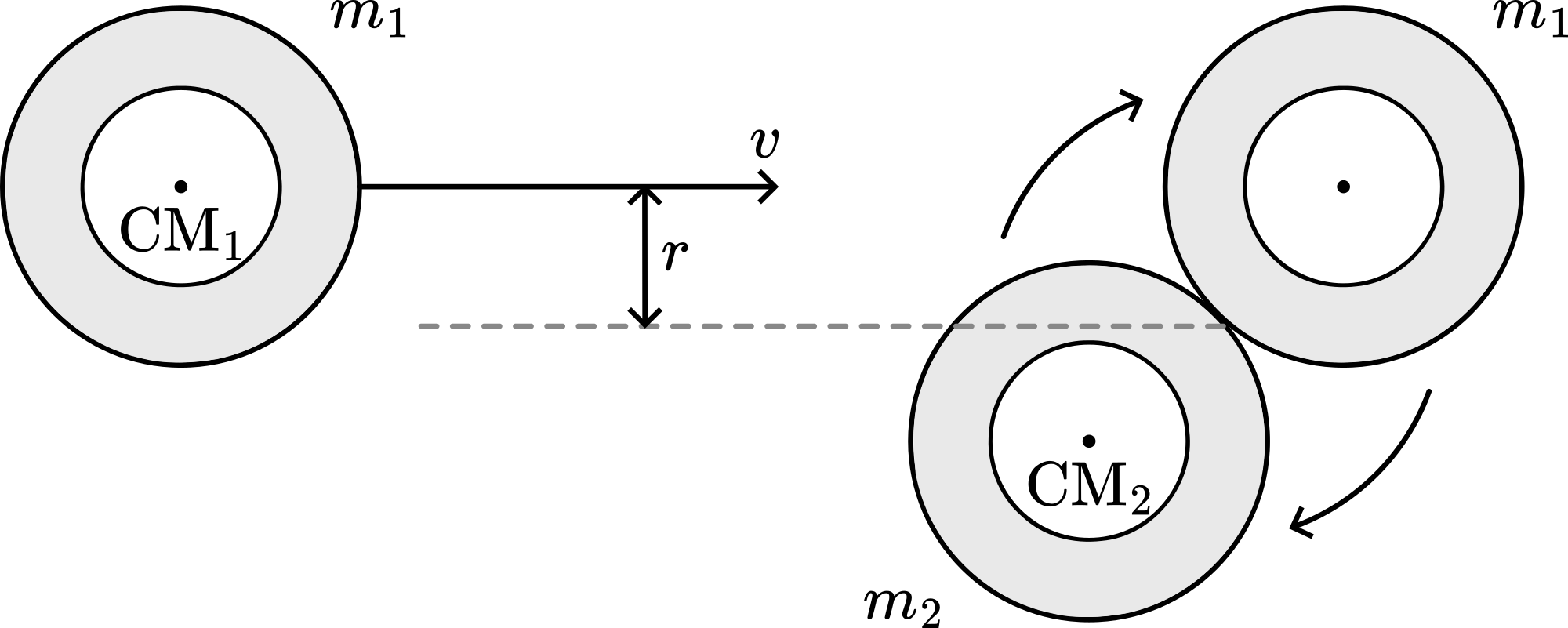
Fig. 215 .#
First we use the pertinax meterstick. The stick hits the plunger of the cart at around \(25 \mathrm{~cm}\) distance from its point of suspension. After the collision, the cart moves along the track and stops at point 1 (see Diagram). This distance is a measure for the amount of kinetic energy the cart got initially at launching. A marker is placed at this point. The procedure is repeated for the stick hitting at 50,67 (corresponding to the percussion point) and \(100 \mathrm{~cm}\). The markers 2, 3 and 4 in the Diagram show the respective distances traveled by the cart. Clearly, the second situation imparts most kinetic energy to the cart, and not the one hitting at the percussion point (marker 3 ). The sequence is repeated, but now also the movement of the meterstick after collision is observed. Students will observe that at \(25 \mathrm{~cm}\), the meterstick continues swinging in the same direction after the collision, while at \(100 \mathrm{~cm}\) the meterstick bounces back. Asking what will happen at around \(50 \mathrm{~cm}\) will make them easily predict that the meterstick will stand still after the collision. Next this can be verified.
The whole experiment can be repeated with the heavier aluminum stick. This will show a sweet spot at the end of the stick \((100 \mathrm{~cm})\).
Explanation#
See Figure 216.
Supposing that the collision is completely elastic, we apply conservation of angular momentum and conservation of energy.
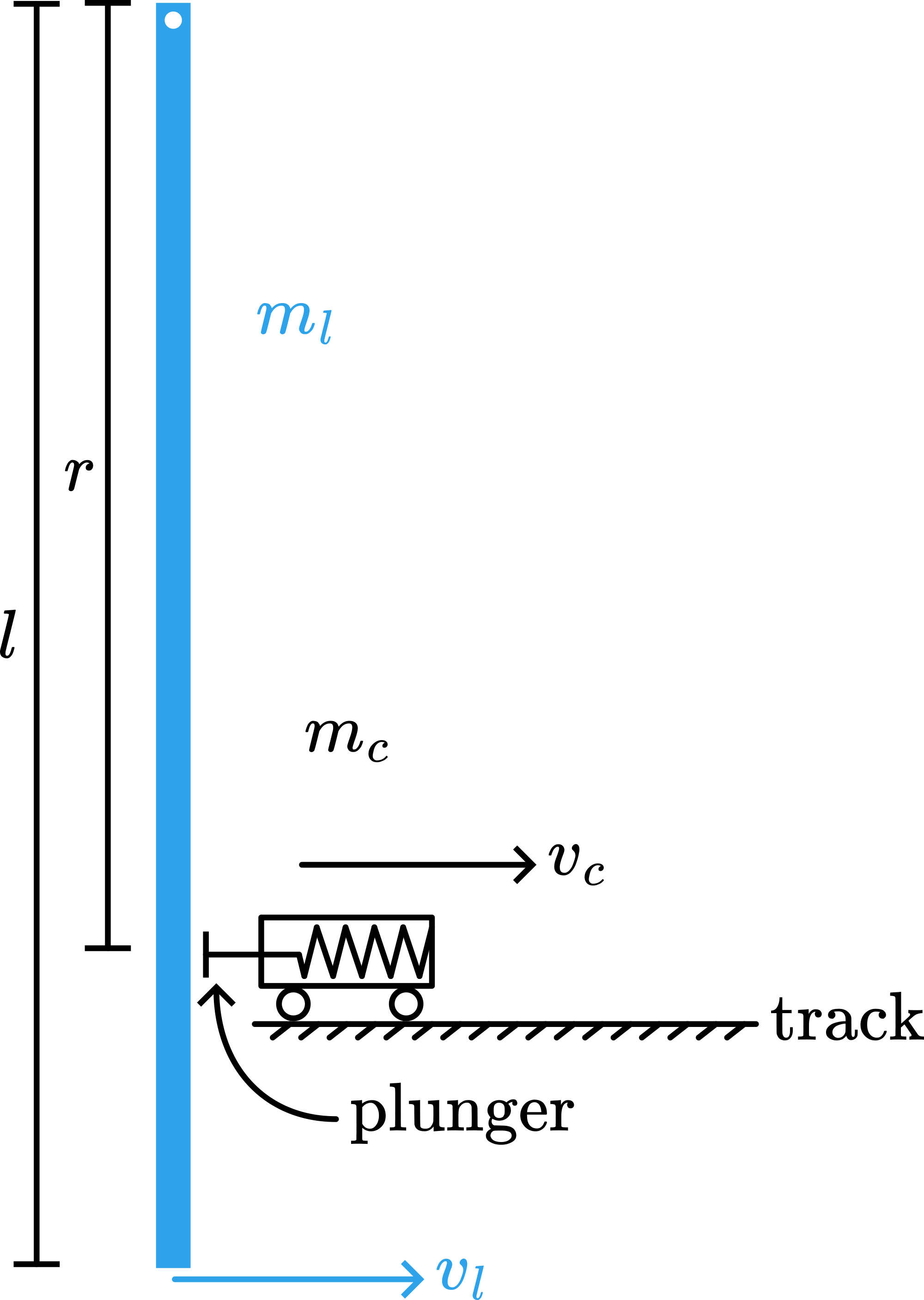
Fig. 216 .#
Conservation of angular momentum: \(\frac{1}{3} m_{l} l v_{l}=\frac{1}{3} m_{l} l v_{l}^{'}+m_{c} r v_{c}\) ( \(v^{'}\) being the velocity of the meterstick after collision)
Conservation of kinetic energy: \(\frac{1}{6} m_{l} v_{l}^{2}=\frac{1}{6} m_{l} v_{l}^{' 2}+\frac{1}{2} m_{c} v_{c}^{2}\).
In this elastic collision the meterstick will have transferred all its kinetic energy to the cart if after the collision \(v^{'}=0\). Then the equation of angular momentum gives:
\(v_{c}=\frac{1}{3} \frac{m_{l}}{m_{c}} \frac{l}{r} v_{l}\), and this combined with the energy-equation: \(\frac{1}{6} m_{l} v_{l}^{2}=\frac{1}{2} m_{c} v_{c}^{2}\) will give
\(r=\sqrt{\frac{1}{3} \frac{m_{l}}{m_{c}}} l\). So the point on the stick of maximum energy transfer (sweet spot)
depends on the mass-relationship between stick (baseball bat) and cart (ball).
Applying the masses of the meter sticks and cart used in our demonstration we find \(r_{\text {pertinax }}=52 \mathrm{~cm}\) and \(r_{\text {aluminum }}=103 \mathrm{~cm}\) (in correspondence to our presentation).
Remarks#
Repeating the same situation a couple of times will show a distribution in the results of how far the cart rolls before it stops. In our demonstration this distribution is not disturbing the “one-run” presentations. However, take care not to take the different \(r\)-distances too close to each other.
As \(r=\sqrt{\frac{1}{3} \frac{m_{l}}{m_{c}}} l\) shows, the sweet spot and percussion point will be the same distance \(r\) at \(m_{c}=\frac{3}{4} m_{l}\).
The vertical shafts are not round but square. This enables easy positioning when shifting a pendulum up or down.
Sources#
PASCO scientific, Instruction Manual and Experiment Guide, pag. ME9430, exp.5
