07 Nutation (2)#
Aim#
To give a geometric description of nutation
Subjects#
1Q50 (Gyros)
Diagram#

Fig. 256 .#
Equipment#
Model (see Diagram and Figures).
Presentation#
Watching a nutating object we observe that the body-axis makes a conical movement (see Nutation. This movement of the body-axis is visualized in our model by rotating the \(L\)-axis by hand (see Figures).
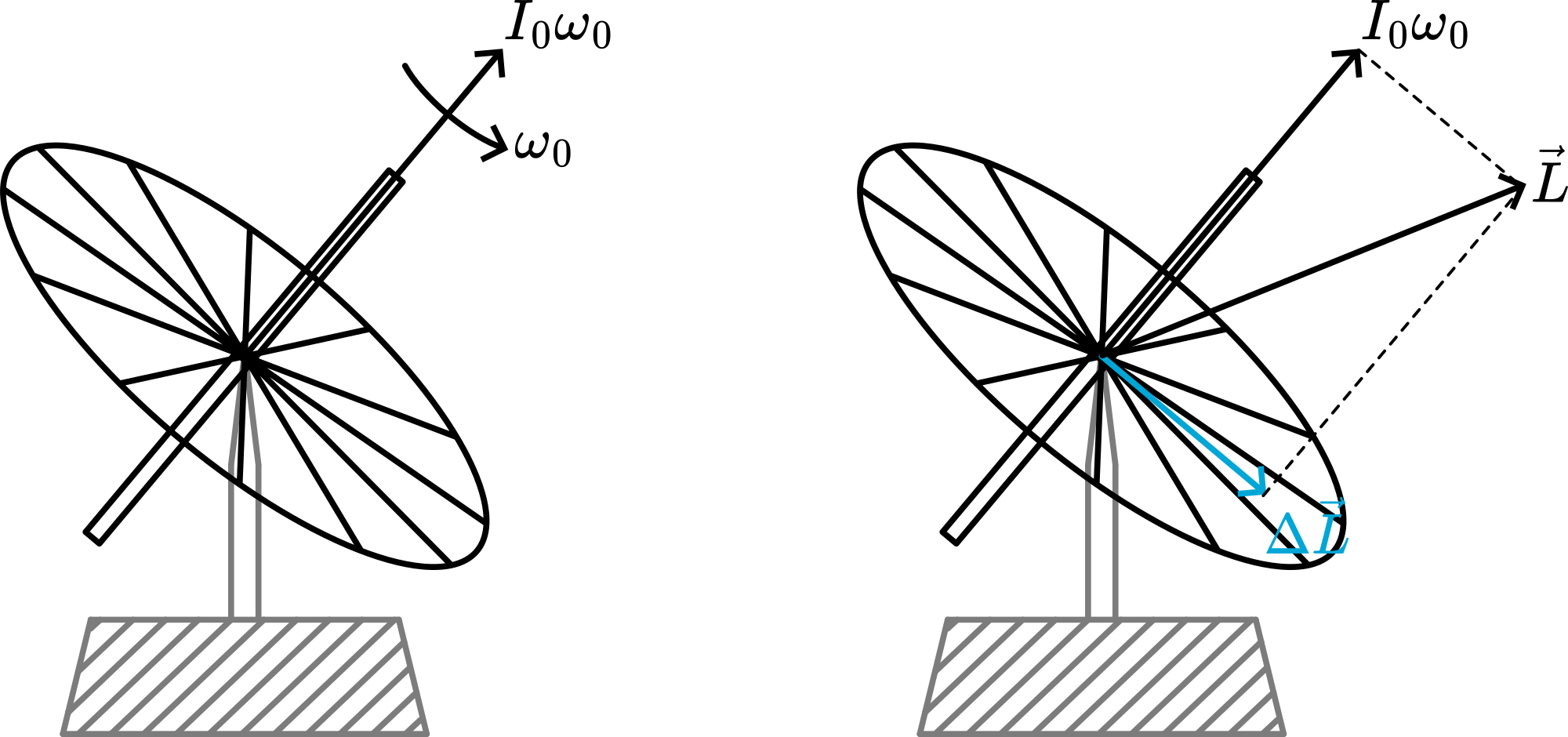
Fig. 257 .#
Explanation#
\(L\), wand body-axis are in one plane. While moving, \(L\) remains fixed in space, so movement of that plane has to take place around \(L\).
The fixed cone (so-called “space cone”) contains wand this \(\omega\) turns around \(L\). To show the position of \(\omega\) with rerspect to the body axis, a cone around the body-axis (so-called body-cone) is visualized. This body-cone also contains \(\omega\). So in our model the position of \(\omega\) is seen where the two cones touch each other. While rotating, the movement of the body-axis around \(L\) (nutation) and the movement of the momentary rotation-axis \((\omega)\) around the symmetry-axis can be observed.
Remarks#
The model is made in such a way that the two cones grip each other (teeth on the inside of the rim of the body-cone grip the wooden bars of the space-cone), so that the cones are not slipping. This is needed since there is only one \(\omega\) while in our model \(\omega\) is in two cones.
Our model represents the movement of a disk-shaped nutating object \(\left(I_{3}>I_{1}\right)\). Visualizing of a nutating bar-shaped object \(\left(I_{1}>I_{3}\right)\) needs a model having the body-cone revolving with its outside around a fixed space-cone.
Sources#
Borghouts, A.N., Inleiding in de Mechanica, pag. 224-227
Roest, R., Inleiding Mechanica, pag. 222-226 Nutation (2)
