01 Physical Pendulum (1) Compound Pendulum#
Aim#
To show and discuss the characteristics of a physical pendulum: reduced length, reversion pendulum and minimal period.
Subjects#
3A15 (Physical Pendula)
Diagram#
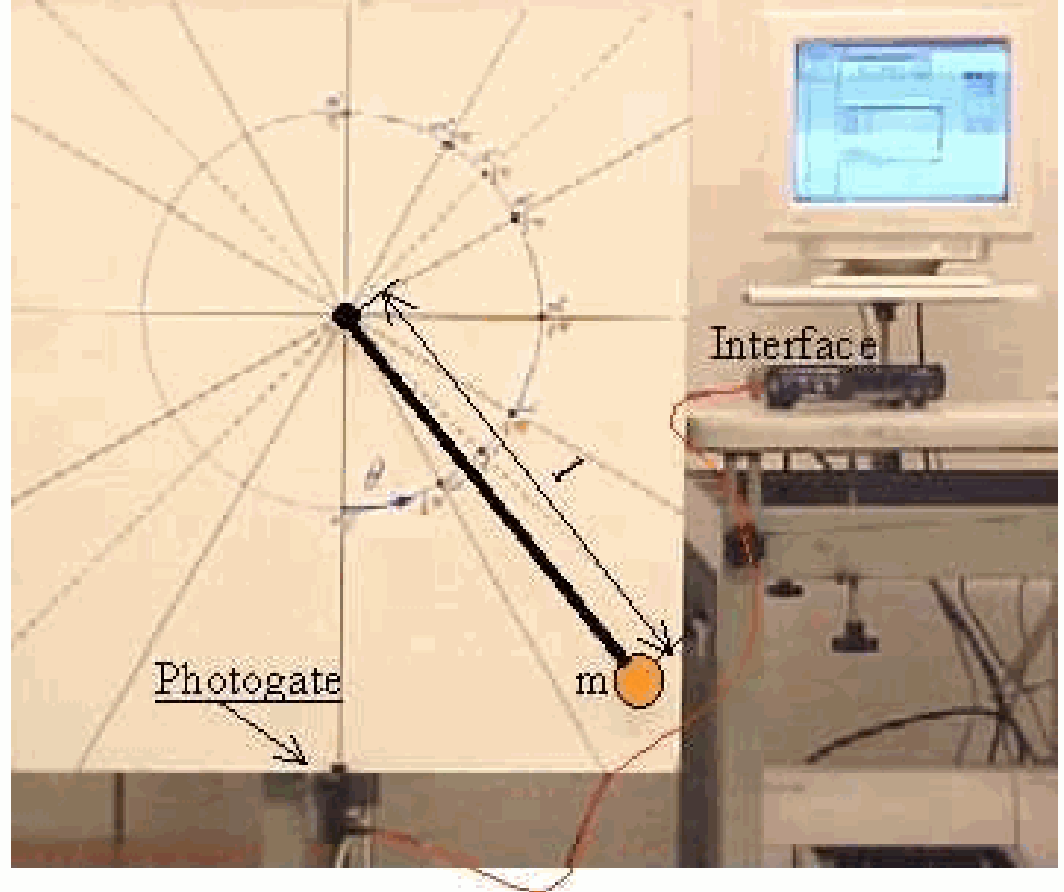
Fig. 301 .#
Equipment ‘#
2 meter sticks; \(I=1 \mathrm{~m}\), with holes for reversed pendulum and minimum pendulum. (One of the sticks has extra holes at \(s=20 \mathrm{~cm}\) and \(s=40 \mathrm{~cm}\) (see PresentationXX 3.)
2 axes in a ball-bearing.
1 mathematical pendulum ( \(l=.667 \mathrm{~m}\) ).
1 meter stick for measurements.
Presentation#
The physical pendulum is suspended on an axis at hole A. A mathematical pendulum is swinging and given such a length that its period equals that of the physical pendulum. Its length is measured and it shows \(67 \mathrm{~cm}\).
Now the physical pendulum is suspended on the axis at hole \(B\). Its period shows to be the same as both foregoing pendulums. The length of the pendulum below \(B\) is measured and it shows that this length equals the length of the mathematical pendulum!
The pendulum is suspended at hole \(D\). Now \(T\) is shorter than in the foregoing demonstrations. Evidently there is a minimum between A and B.
This can be demonstrated when both pendulums are suspended: one at \(D\) and the other in one of the extra holes on either side of \(D\) (between \(A\) and B). When both pendulums start together, after only a few oscillations it is clear that \(D\) is the faster pendulum.
Explanation#
For a physical pendulum with mass \(m\), oscillating around its suspension in point A, we can write for the period: \(T=2 \pi \sqrt{\frac{I_{A}}{m g S}}\) (see Figure 302 \(I_{A}\) being the moment of inertia, and \(s\) being the distance between the centre \(l_{M}\) of mass and the axis of rotation).
When the physical pendulum is a long uniform stick of length \(l_{F}\) its moment of inertia is \(I_{c}=\frac{1}{12} m l_{F}^{2}\) and when it oscillates around a point A a distance \(s=\frac{1}{2} l_{f}\) away from \(C\), then \(I_{A}=\frac{1}{12} m l^{2}+m\left(\frac{1}{2} l\right)^{2}\), so: \(I_{A}=\frac{1}{3} m l_{F}^{2}\). The period of the pendulum becomes: $\(T_{F}=2 \pi \sqrt{\frac{\frac{1}{3} m l_{F}^{2}}{\frac{1}{2} m g l_{F}}}=2 \pi \sqrt{\frac{2}{3} \frac{l_{F}}{g}}\)$
A mathematical pendulum of length \(l_{M}\) has a moment of inertia
\(I_{A}=m l_{M}^{2}\) and so: $\(T_{M}=2 \pi \sqrt{\frac{m l_{M}^{2}}{m g l_{M}}}=2 \pi \sqrt{\frac{l_{M}}{g}}\)$
When we want \(T_{F}=T_{M}\), then we need that \(l_{M}=\frac{2}{3} l_{F}\). This \(l_{M}\) is called the reduced length of the physical pendulum.

Fig. 302 .#
When the physical pendulum is suspended in a point \(B\), such that its remaining length is \(l_{M}\), then again the period is the same! (See Figure 303)
\(T=2 \pi \sqrt{\frac{I_{B}}{m g s}}\)
\(I_{B}=\frac{1}{12} m l_{F}^{2}+m s^{2}\) \(s=l_{M}-\frac{1}{2} l_{F}\)
and with \(l_{M}=\frac{2}{3} l_{F}\), and \(s=\frac{1}{6} l_{F}\), we find: \(I_{B}=\frac{1}{12} m l_{F}^{2}+\frac{1}{36} m l_{F}^{2}=\frac{1}{9} m l_{F}^{2}\).
Then the period will be: \(T=2 \pi \sqrt{\frac{\frac{1}{9} m l_{F}^{2}}{\frac{1}{6} m g l_{F}}}=2 \pi \sqrt{\frac{2}{3} \frac{l_{F}}{g}}\)
So this pendulum has the same reduced length and the same period as the physical pendulum shown in the first presentation.
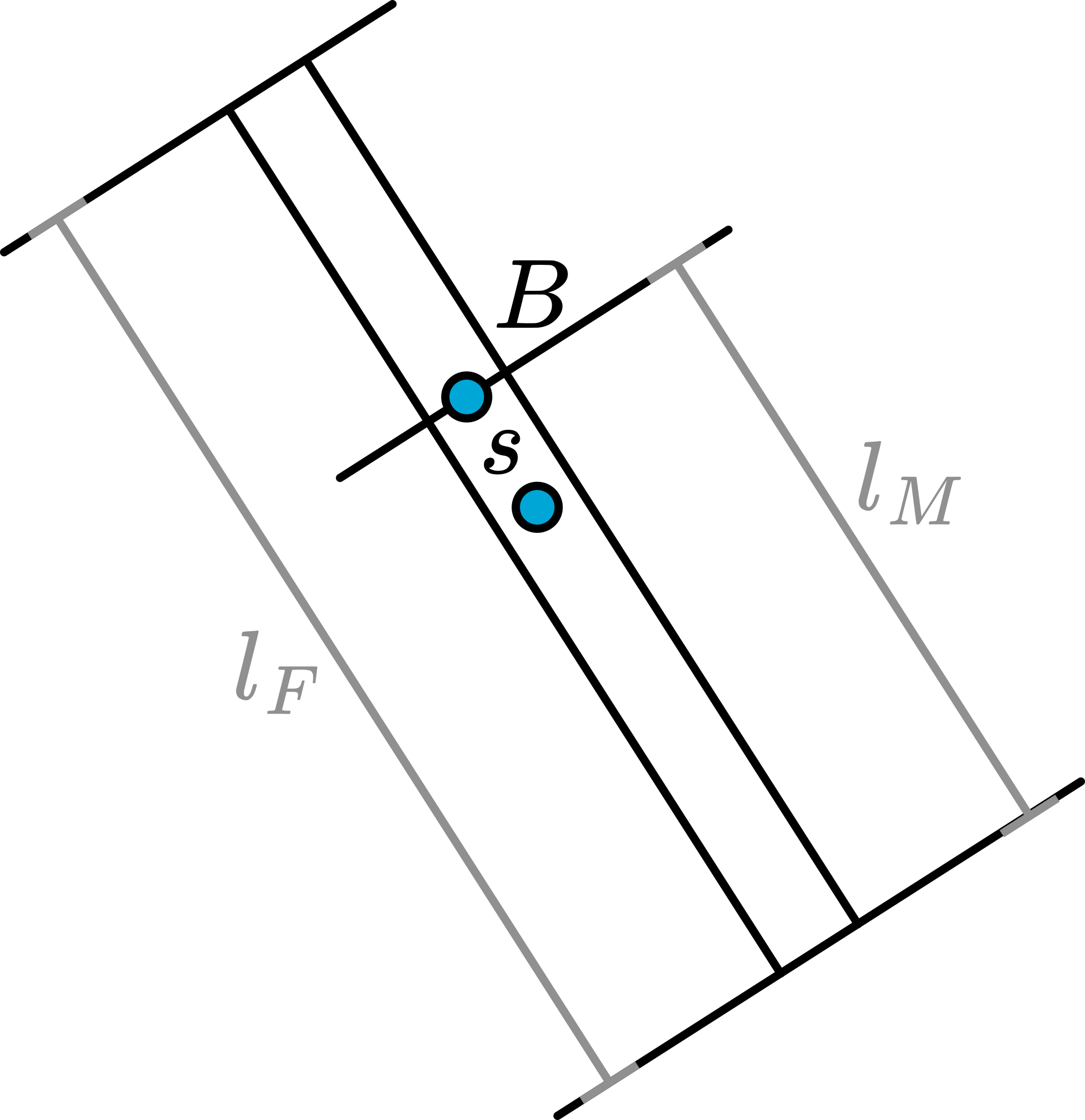
Fig. 303 .#
Between the suspension of \(A\) and \(B\) the presentation shows that a minimum period appears (suspension at D; see Diagram).
Now: \(T=2 \pi \sqrt{\frac{I_{D}}{m g s}}\) (D being some point at \(s\) away from C.)
\(I_{d}=I_{c}+m s^{2}\) and with \(I_{c}=\frac{1}{12} m l_{F}^{2}\) we find:
\(T=2 \pi \sqrt{\frac{\frac{1}{12} m l_{F}^{2}+m s^{2}}{m g s}}=\sqrt{\frac{2 \pi}{\sqrt{g}} \sqrt{\frac{l_{F}}{12 s}+1}}\)
\(T\) being a minimum for \(\frac{d T}{d s}=0\), we find: \(s=\frac{l_{F}}{\sqrt{12}}\).
The length of the stick ( \(l_{F}\) ) is 1 meter, so \(s\) equals \(\frac{1}{\sqrt{12}}=0.289\) meters.
Remarks#
In order to give the physical pendulum a length of 1 meter and yet have a hole at the ends of this stick, we have triangularly shaped the ends (see Figure 304).

Fig. 304 .#
The differences in \(T\) are small. With \(I_{F}=1\) meter, we find: \(T_{A}\left(=T_{B}\right)=1.64\) sec. And \(T_{D}=1.52 \mathrm{sec}\).
To obtain larger \(T\) s a suspension closer to \(\mathrm{C}\) is needed.
Calculating: at \(s=12.5 \mathrm{~cm}\left(1 / 8 l_{F}\right), T=1.78 \mathrm{sec}\).;
at \(s=8.3 \mathrm{~cm},\left(1 / 12 l_{F}\right), T=2.09 \mathrm{sec}\);
\(s=2.0 \mathrm{~cm}, T=4.1 \mathrm{sec}\);
\(s=1.0 \mathrm{~cm}, T=5.8 \mathrm{sec}\).
Of course at \(s=0, T=\) infinitive.
\(T=2 \pi \sqrt{\frac{I_{A}}{m g s}}\) shows that physical pendulums of the same mass have
different periods due to their \(I / s\)-ratio. Comparing different pendulums can be done when comparing that ratio.
For a long uniform stick this reduces to comparing the \(I_{F} / s\)-ratio
Sources#
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 154-156 and 161-162
Meiners, Harry F., Physics demonstration experiments, part I, pag. 277-278
Roest, R., Inleiding Mechanica, pag. 168-169
