01 Force Effect of Current#
Aim#
To show that when a current is flowing in a wire, parts of the wire exert forces on one another.
Subjects#
5H40 (Force on Current Wires)
Diagram#
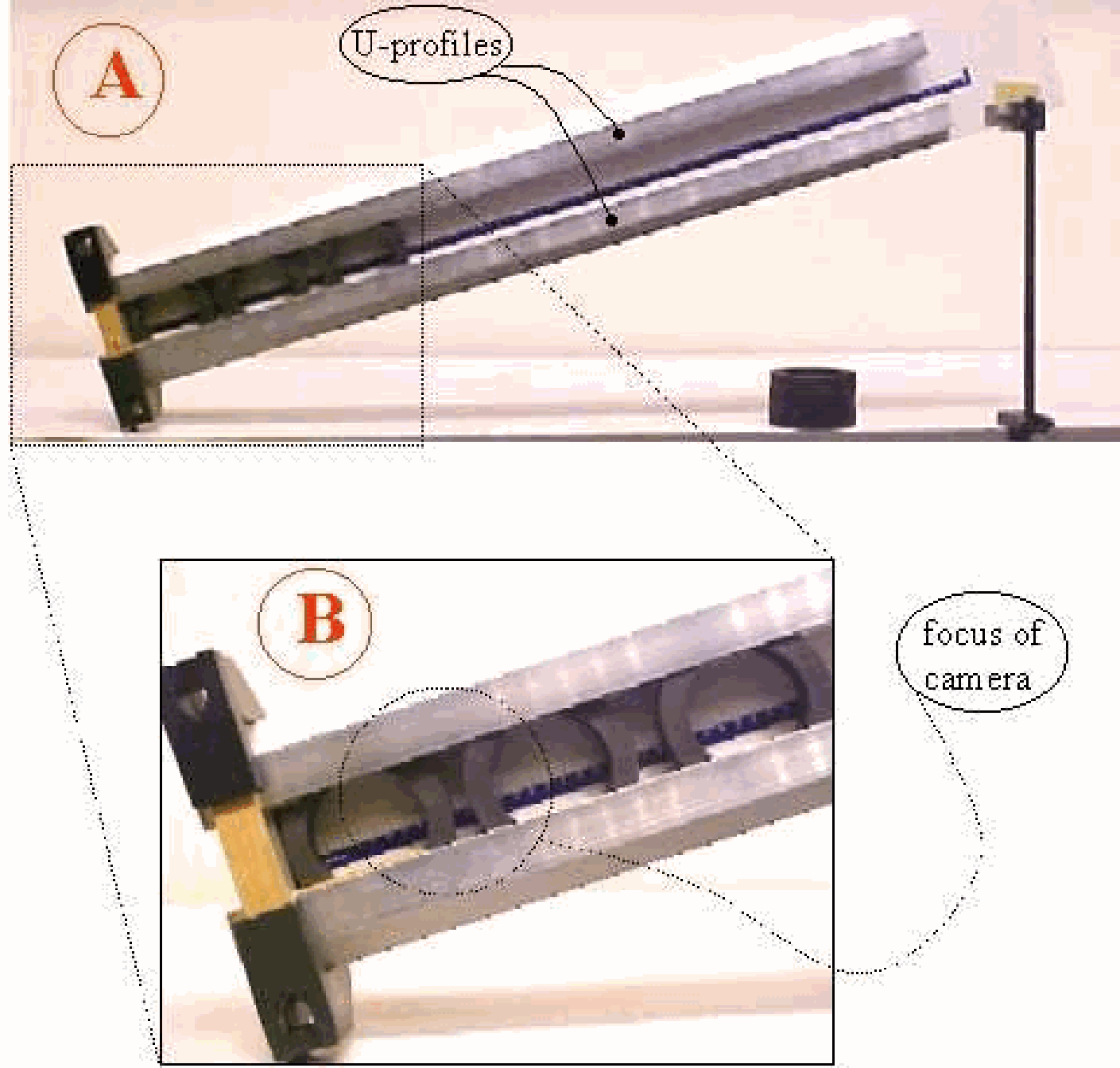
Fig. 505 .#
Equipment#
Power supply, we use \(1.2 \mathrm{kV} / .2 \mathrm{~A}\).
Capacitor, we use \(2200\mathrm{~uF}/500\mathrm{~Vdc}\).
High current switch.
Unipolar switch.
V-meter, large scale.
Wire, \(2 \mathrm{~m}\).
Power supply, \(100\mathrm{~A}\).
Presentation#
First connect the \(2 \mathrm{~m}\)-wire to the 100A powersupply. Position the wire-parts close together (see Figure 506A). Switch on the powersupply and see how the wire-parts move away from each other.

Fig. 506 .#
To make this effect stronger, we use the demonstration as shown in Diagram and Figure 507A. First the capacitor is charged to \(500 \mathrm{~V}\). Then switch \(\mathrm{S}_{1}\) is opened and the high current switch is closed. The wire-parts fly away from each other (Figure 507B).
Fig. 507 .#
Ask the students what shape the wire loop would take if such a high current should flow continuously.
Explanation#
The first part of the demonstration shows that opposing currents exert a repelling force on each other. Moreover, the demonstration shows how small this force effect of current is.
On this force effect the definition of the Ampere as the unit of electric current is based \(\frac{\Delta F}{\Delta l}=2 \times 10^{-7} \frac{I_{1} I_{2}}{r}\). This demonstration, using \(\mathrm{I}_{1}=\mathrm{I}_{2}=100 \mathrm{~A}\) and \(\Delta l=1 \mathrm{~m}\) has to deal with a force of only \(2 \cdot 10^{-3} \mathrm{~N}\). No wonder the displacement of the wire is small.
In the second part of the demonstration the current is much higher. Supposing the wire and contacts having a resistance of \(0.5 \Omega\), a current of \(1000 \mathrm{~A}\) is flowing in the beginning of the discharge. Then the force on the wireloop is . \(2 \mathrm{~N}\). This hundredfold higher force exists only a short time. Not only F diminishes due to the increasing distance, but also due to the reducing discharge current (the circuit has a RC-time of about \(1 \mathrm{msec}\) ). Due to its impulse the wire-parts continue to move after the discharge (Figure 507B).
If current should flow continuously the wire would take the shape of a perfect circle.
Remarks#
Mind that when using the \(100\mathrm{~A}\) power supply that the 100A is not interrupted abruptly, because when this happens the high induced voltages can damage the power supply.
Sources#
Biezeveld, H. and Mathot, L., Scoop, Natuurkunde voor de bovenbouw, part 4/5 vwo, pag. 220
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 407 and 411
